��啨��'09�N[3]
�����̋��@�A�@�����@�\�@�ɂ��Ă͂܂鐔������B�������A�p�x����ъp���x�̒P�ʂ́A���ꂼ��rad�����rad/s�Ƃ��A�~������π�Ƃ���B�K�v������A�O�p���̌���
��p���Ă悢�B�܂��Aθ �̑傫�����\���������Ƃ��ɂ́A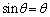 �C
�C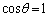 �Ƃ���B
�Ƃ���B
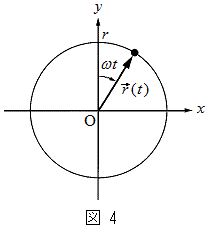 ��1�@�}4�̂悤�ɁAxy���ʏ�Ŏ��v���Ɋp���x�̑傫����ω �œ����~�^�������镨�̂��l����Bxy���W�̌��_���~�̒��S�Ƃ��A����t�ł̕��̂̈ʒu
��1�@�}4�̂悤�ɁAxy���ʏ�Ŏ��v���Ɋp���x�̑傫����ω �œ����~�^�������镨�̂��l����Bxy���W�̌��_���~�̒��S�Ƃ��A����t�ł̕��̂̈ʒu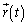 ��
��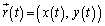 �ƕ\���B�������A�~�̔��a��r�Ƃ��A����0�ł�
�ƕ\���B�������A�~�̔��a��r�Ƃ��A����0�ł�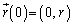 �Ƃ���B���l�ɁA���x
�Ƃ���B���l�ɁA���x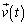 ��
��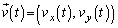 �C�����x
�C�����x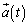 ��
��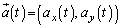 �ƕ\���B�����́Ar�Cω�Ct�̒�����K�v�ȋL����p���ĕ\���B
�ƕ\���B�����́Ar�Cω�Ct�̒�����K�v�ȋL����p���ĕ\���B����t�ł̕��̂̈ʒu�ɂ��ẮA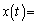 �@�A�@�C
�@�A�@�C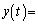 �@�C�@�ł���B����0����
�@�C�@�ł���B����0����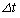 �܂ł̈ʒu�̕ω�
�܂ł̈ʒu�̕ω�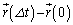 �́A
�́A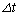 ���\���������Ƃ��ɂ�
���\���������Ƃ��ɂ�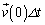 �ɓ������̂ŁA
�ɓ������̂ŁA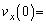 �@�E�@�C
�@�E�@�C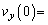 �@�G�@�ł���B
�@�G�@�ł���B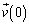 ��
��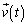 �̂Ȃ��p��
�̂Ȃ��p��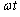 �ł��邩��A
�ł��邩��A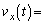 �@�I�@�C
�@�I�@�C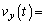 �@�J�@�ƂȂ�B���l�ɁA���x�̕ω�
�@�J�@�ƂȂ�B���l�ɁA���x�̕ω�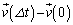 ��
��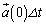 �ɓ������̂ŁA
�ɓ������̂ŁA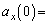 �@�L�@�C
�@�L�@�C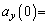 �@�N�@�ł���B
�@�N�@�ł���B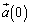 ��
��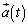 �̂Ȃ��p��
�̂Ȃ��p��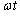 �ł��邩��A
�ł��邩��A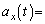 �@�P�@�C
�@�P�@�C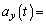 �@�R�@�ƂȂ�B
�@�R�@�ƂȂ�B  ��2�@�}5�̂悤�ɁA����m�̑����̕��̂��A���ʂ������ł���o�l�萔k�̓����o�l�łȂ��A�Ȃ߂炩�Ȑ����ʏ�̒���(x��)�ɉ����ĐÎ~������B���̂Ƃ��A�e���̂̊Ԋu��d�ł���A���[����n�Ԗڂ̕��̂̈ʒu
��2�@�}5�̂悤�ɁA����m�̑����̕��̂��A���ʂ������ł���o�l�萔k�̓����o�l�łȂ��A�Ȃ߂炩�Ȑ����ʏ�̒���(x��)�ɉ����ĐÎ~������B���̂Ƃ��A�e���̂̊Ԋu��d�ł���A���[����n�Ԗڂ̕��̂̈ʒu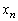 ��
��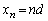 �Ƃ���B���ɁA���ꂼ��̕��̂�U��r�C�p�U����ω ��x�����ɒP�U��������B����t�ɂ����āAn�Ԗڂ̕��̂��͂��߂ɐÎ~���Ă����ʒu
�Ƃ���B���ɁA���ꂼ��̕��̂�U��r�C�p�U����ω ��x�����ɒP�U��������B����t�ɂ����āAn�Ԗڂ̕��̂��͂��߂ɐÎ~���Ă����ʒu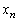 ����̕ψʂ�
����̕ψʂ�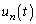 �Ƃ���B�ȉ��ł́A���ׂĂ̕��̂̕ψʂ��}6�Ɏ����悤�ɔg��λ�̐����g��ɂ���A���Ԃ̌o�߂ɂ��������āA���̐����g��x���̐��̌����ɐi�ޏꍇ���l����B���̂Ƃ��Aλ��d�ɂ���ׂď\���ɑ傫���A���̂ɍ�p����͂̓o�l�ɂ����݂̂̂Ƃ���B �����́Ar�Cω�Ct�Cd�Cλ�Cm�Ck�̒�����K�v�ȋL����p���ĕ\���B
�Ƃ���B�ȉ��ł́A���ׂĂ̕��̂̕ψʂ��}6�Ɏ����悤�ɔg��λ�̐����g��ɂ���A���Ԃ̌o�߂ɂ��������āA���̐����g��x���̐��̌����ɐi�ޏꍇ���l����B���̂Ƃ��Aλ��d�ɂ���ׂď\���ɑ傫���A���̂ɍ�p����͂̓o�l�ɂ����݂̂̂Ƃ���B �����́Ar�Cω�Ct�Cd�Cλ�Cm�Ck�̒�����K�v�ȋL����p���ĕ\���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��1�ł́A�ߎ��v�Z�𑣂��悤�ȗU�������Ă��܂����A�������Ƃ��Ă͋��ȏ������`��������Ƃ��Ă��A��[���ʼn�@������邱�Ƃ��Ȃ��A�ߎ��O�̌��ʂ�����Ă��炸�A���͔������ĉ����OK�ł�(�ψʁE���x�E�����x���Q��)�B
��2(�Z)�͕�������₱�����̂Œ��ӂ��Ă��������B
��1�@���̖��ł���]�p��y�����������玞�v���ɑ����Ă��܂����Ay���������Ax�����c���ɂƂ��Č���Ax�����������甽���v�����p�𑪂�ꍇ�ƁAx���W��y���W������ւ���Ă��邾���ł�(�����~�^�����Q��)�B (�A) 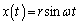 ......[��]
......[��]
(�C) 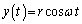 ......[��]���̂����x
......[��]���̂����x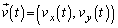 �ɂ��āA
�ɂ��āA 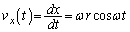 �C
�C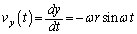
(�E) 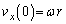 ......[��]
......[��]
(�G) 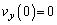 ......[��]
......[��]
(�I) 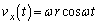 ......[��]
......[��]
(�J) 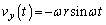 ......[��]���̂������x
......[��]���̂������x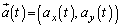 �ɂ��āA
�ɂ��āA 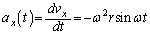 �C
�C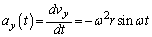
(�L) 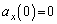 ......[��]
......[��]
(�N) 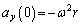 ......[��]
......[��]
(�P) 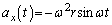 ......[��]
......[��]
(�R) 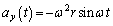 ......[��]���D��蕶�̗U���͖�2�Ƃ̊֘A�Ō����ƁA���x�x�N�g��
......[��]���D��蕶�̗U���͖�2�Ƃ̊֘A�Ō����ƁA���x�x�N�g��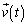 ���ʒu�x�N�g��
���ʒu�x�N�g��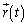 �����ʑ���
�����ʑ���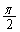 �i��ł��āA�����x�x�N�g��
�i��ł��āA�����x�x�N�g��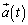 �����x�x�N�g��
�����x�x�N�g��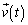 �����ʑ���
�����ʑ���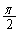 �i��ł����A����t�ɂ��������x
�i��ł����A����t�ɂ��������x �C�����x
�C�����x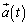 �́A����0�ɂ��������x
�́A����0�ɂ��������x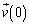 �C�����x
�C�����x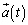 ��
��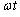 ������]���������̂��A�ƁA���������̂��낤�Ǝv���܂��B
������]���������̂��A�ƁA���������̂��낤�Ǝv���܂��B
��2(�T) P�Ԗڂ̕��̂�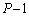 �Ԗڂ̕��̂��ʑ����A�܂��A
�Ԗڂ̕��̂��ʑ����A�܂��A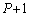 �Ԗڂ̕��̂�P�Ԗڂ̕��̂��ʑ����́A����d�C�g��λ���A
�Ԗڂ̕��̂�P�Ԗڂ̕��̂��ʑ����́A����d�C�g��λ���A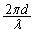 �ł��B
�ł��B �����̌o�߂ɏ]���āA�����g��x���������ɐi�ނ̂ŁA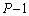 �Ԗڂ̕��̂��ψ���P�Ԗڂ̕��̂��ψ������A�ʑ���
�Ԗڂ̕��̂��ψ���P�Ԗڂ̕��̂��ψ������A�ʑ���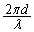 �����i��ł��āAP�Ԗڂ̕��̂��ʑ���
�����i��ł��āAP�Ԗڂ̕��̂��ʑ���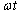 �Ȃ�A
�Ȃ�A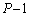 �Ԗڂ̕��̂��ʑ���
�Ԗڂ̕��̂��ʑ���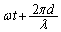 �ł��B�܂�A
�ł��B�܂�A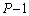 �Ԗڂ̕��̂ɑΉ����������~�^������]�p�́A
�Ԗڂ̕��̂ɑΉ����������~�^������]�p�́A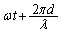 ......[��]
......[��] (�V) ���l�ɁA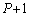 �Ԗڂ̕��̂��ψ���P�Ԗڂ̕��̂��ψ������A�ʑ���
�Ԗڂ̕��̂��ψ���P�Ԗڂ̕��̂��ψ������A�ʑ���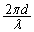 �����x��Ă��āAP�Ԗڂ̕��̂��ʑ���
�����x��Ă��āAP�Ԗڂ̕��̂��ʑ���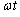 �Ȃ�A
�Ȃ�A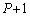 �Ԗڂ̕��̂��ʑ���
�Ԗڂ̕��̂��ʑ���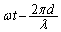 �ł��B�܂�A
�ł��B�܂�A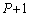 �Ԗڂ̕��̂ɑΉ����铙���~�^������]�p�́A
�Ԗڂ̕��̂ɑΉ����铙���~�^������]�p�́A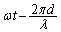 ......[��]
......[��] (�X) 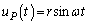 ���1��
���1��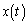 �Ɠ��l�ɍl���āAP�Ԗڂ̕��̂������x
�Ɠ��l�ɍl���āAP�Ԗڂ̕��̂������x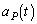 �́A
�́A 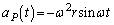 ......[��]
......[��](�Z) 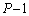 �Ԗڂ̕��̂�P�Ԗڂ̕��̂̊Ԃ̃o�l���L��
�Ԗڂ̕��̂�P�Ԗڂ̕��̂̊Ԃ̃o�l���L��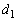 �́A
�́A P�Ԗڂ̕��̂������̃o�l��������́A�����ɒ��ӂ��āA
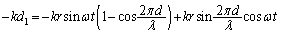 �@����@
�@����@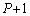 �Ԗڂ̕��̂�P�Ԗڂ̕��̂̊Ԃ̃o�l���L��
�Ԗڂ̕��̂�P�Ԗڂ̕��̂̊Ԃ̃o�l���L��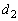 �́A
�́AP�Ԗڂ̕��̂��E���̃o�l��������́A�����ɒ��ӂ��āA
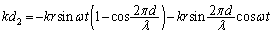 �@����A
�@����A�@�{�A���AP�Ԗڂ̕��̂����E�̃o�l��������������́A
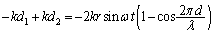 �@����B
�@����B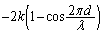 ......[��]
......[��]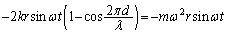
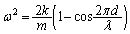 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B