��啨��'10�N�O��[2]
�d�C�͐��ɂ��čl�@���悤�B�^�ɒu���ꂽ�d�C��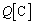 (
(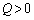 )�̐��̓_�d�ׂ��甭������d�C�͐��̑��{��N��Q�ɔ�Ⴗ��B�����ŁA���W��A��p����
)�̐��̓_�d�ׂ��甭������d�C�͐��̑��{��N��Q�ɔ�Ⴗ��B�����ŁA���W��A��p����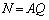 �ŗ^������Ƃ��悤�B�܂��A�_�d�ׂ��甭������d�C�͐��́A�S�Ă̕����ɓ��������ˏ�ɍL����B���̂Ƃ��A�d��(�d�E)�̋���
�ŗ^������Ƃ��悤�B�܂��A�_�d�ׂ��甭������d�C�͐��́A�S�Ă̕����ɓ��������ˏ�ɍL����B���̂Ƃ��A�d��(�d�E)�̋���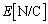 �́A�d�C�͐��ɐ����Ȗʂ��l���A�����ʉ߂���d�C�͐��̒P�ʖʐϓ�����̖{��n�ɔ�Ⴗ��B�����ŁA���W��B��p����
�́A�d�C�͐��ɐ����Ȗʂ��l���A�����ʉ߂���d�C�͐��̒P�ʖʐϓ�����̖{��n�ɔ�Ⴗ��B�����ŁA���W��B��p����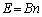 �ŗ^������Ƃ��悤�B�d��x�N�g���̌����͓d�C�͐��̌����ɓ������B����A���̓d�C�ʂ̓_�d�ׂɑ���d�C�͐��͌������t�ɂȂ�B�����̂��Ƃ܂��Ĉȉ��̖₢�ɓ�����B�Ȃ��A�ɂ͌W��A�CB��p���Ă悢���A��蒆�ŗ^�����Ă��Ȃ��L����p���Ă͂Ȃ�Ȃ��B
�ŗ^������Ƃ��悤�B�d��x�N�g���̌����͓d�C�͐��̌����ɓ������B����A���̓d�C�ʂ̓_�d�ׂɑ���d�C�͐��͌������t�ɂȂ�B�����̂��Ƃ܂��Ĉȉ��̖₢�ɓ�����B�Ȃ��A�ɂ͌W��A�CB��p���Ă悢���A��蒆�ŗ^�����Ă��Ȃ��L����p���Ă͂Ȃ�Ȃ��B
�T�D�}1�̂悤�ɁA���_O�ɓd�C��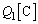 (
(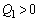 )�̓_�d�ׂ�u�����B
)�̓_�d�ׂ�u�����B ��1�@�_�d��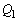 ���狗��
���狗��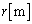 �̓_�ɂ�����d��x�N�g���ɂ��āA���a����(���ar�̋��ʂɐ�����r����������)�̐����������B
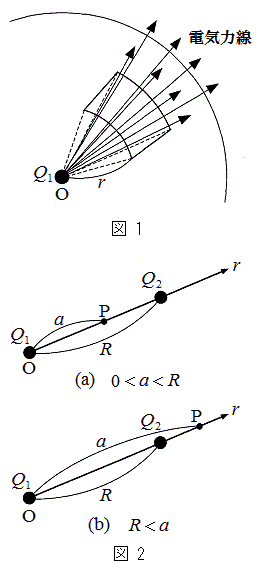
�̓_�ɂ�����d��x�N�g���ɂ��āA���a����(���ar�̋��ʂɐ�����r����������)�̐����������B ��2�@�}2(a)�܂���(b)�̂悤�ɁA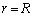 �̂Ƃ���ɓd�C��
�̂Ƃ���ɓd�C��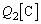 �̂�����̓_�d�ׂ�u�����B���̂Ƃ��A��̓_�d�ׂ�ʂ钼����̓_P�ł̓d��x�N�g���ɂ��āA���a�����̐����������B�������A�_�d��
�̂�����̓_�d�ׂ�u�����B���̂Ƃ��A��̓_�d�ׂ�ʂ钼����̓_P�ł̓d��x�N�g���ɂ��āA���a�����̐����������B�������A�_�d��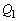 ����_P�܂ł̋�����a�Ƃ��A�}2(a)��
����_P�܂ł̋�����a�Ƃ��A�}2(a)�� �̏ꍇ�Ɛ}2(b)��
�̏ꍇ�Ɛ}2(b)�� �̏ꍇ�ɂ��āA���ꂼ�ꓚ����B
�̏ꍇ�ɂ��āA���ꂼ�ꓚ����B
 �U�D�����������ł��镽��ɓd�ׂz�������ʓd�ׂɂ��čl�@���悤�B�}3�̂悤�ɁA����z���ɐ�����
�U�D�����������ł��镽��ɓd�ׂz�������ʓd�ׂɂ��čl�@���悤�B�}3�̂悤�ɁA����z���ɐ�����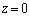 �ɂ���Ax��������y�������ɂ��ꂼ��\���ɍL����
�ɂ���Ax��������y�������ɂ��ꂼ��\���ɍL����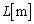 ��
��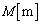 �����B���̕���ɒP�ʖʐϓ�����̓d�C�ʂ�
�����B���̕���ɒP�ʖʐϓ�����̓d�C�ʂ�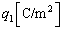 �ƂȂ�悤�ɓd�ׂ���l�ɕ��z�������B�Ȃ��A�ȉ��̖₢�ł͖ʓd�ׂ̂ӂ��̌��ʂ͍l���Ȃ��Ă悢�B
�ƂȂ�悤�ɓd�ׂ���l�ɕ��z�������B�Ȃ��A�ȉ��̖₢�ł͖ʓd�ׂ̂ӂ��̌��ʂ͍l���Ȃ��Ă悢�B��3�@�}3�Ɏ������ʓd�ׂɂ��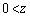 �ł̓d��x�N�g���ɂ��āAz�������̐����������B
�ł̓d��x�N�g���ɂ��āAz�������̐����������B ��4�@�}3�ŗ^����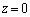 �̖ʓd�ׂɉ����āA�}4�̂悤�ɁA
�̖ʓd�ׂɉ����āA�}4�̂悤�ɁA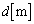 �������ꂽ
�������ꂽ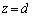 �̂Ƃ���ɓ��l�̖ʓd�ׂ�^�����B�������A�P�ʖʐϓ�����̓d�C�ʂ�
�̂Ƃ���ɓ��l�̖ʓd�ׂ�^�����B�������A�P�ʖʐϓ�����̓d�C�ʂ�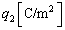 �Ƃ����B���̂Ƃ��A
�Ƃ����B���̂Ƃ��A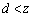 �C
�C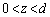 �C
�C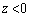 ��3�̗̈�ɂ�����d��x�N�g���ɂ��āAz�������̐��������ꂼ�ꎦ���B
��3�̗̈�ɂ�����d��x�N�g���ɂ��āAz�������̐��������ꂼ�ꎦ���B
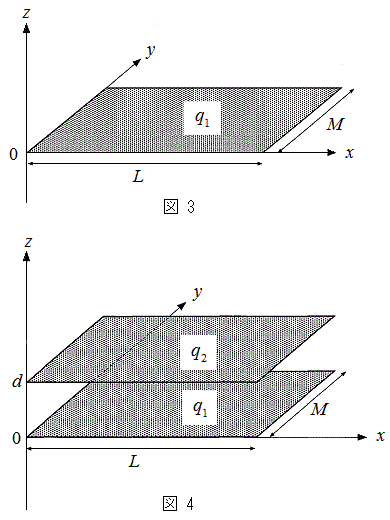
�V�D�}4�ɂ�����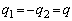 (
(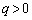 )�Ƃ��A�܂��A��̕��͓��̂łł����ɔƂ���ƁA��̖ʓd�ׂ̓R���f���T�[�̓�̋ɔɒ~����ꂽ�d�ׂƓ������Ȃ�B
)�Ƃ��A�܂��A��̕��͓��̂łł����ɔƂ���ƁA��̖ʓd�ׂ̓R���f���T�[�̓�̋ɔɒ~����ꂽ�d�ׂƓ������Ȃ�B ��5�@��̋ɔ��݂��ɐڐG���Ȃ��͈͂ŏ\���ɐڋ߂�������Ԃ���A�ʊԊud�̏�Ԃ܂ōL����̂ɕK�v�ȃG�l���M�[�������B
��6�@�ʊԊud�̏�Ԃɂ����āA��̋ɔ̊Ԃ̓d�ʍ��̑傫���������B�܂��A���̌��ʂ�p���āA�R���f���T�[�Ƃ��čl�����Ƃ��̓d�C�e�ʂ������B
�W�D�}4�ɂ�����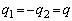 (
(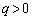 )�Ƃ�����ԂŁA���̂łł����ɔ̊ԂɗU�d�̂�}�������B�U�d�̂̌�����d�Cx��������y�������̕��͋ɔ̃T�C�Y�Ɠ������A���ꂼ��L�CM�Ƃ���B
)�Ƃ�����ԂŁA���̂łł����ɔ̊ԂɗU�d�̂�}�������B�U�d�̂̌�����d�Cx��������y�������̕��͋ɔ̃T�C�Y�Ɠ������A���ꂼ��L�CM�Ƃ���B ��7�@�ɔ̊Ԃ�S�Ė������ʒu�ɗU�d�̂�}�������B���̂Ƃ��A�U�d����(�s���̂̐Ód�U��)�ɂ���ėU�d�̂̏�Ɖ��̖ʂɌ������̖ʓd�ׂ����������B���̌��ʁA��6�ŋ��߂��U�d�̂�}�����Ȃ��ꍇ�ɔ�ׂċɔ̊Ԃ̓d�ʍ��́A���̖ʓd�ׂɂ����f�{�ɂȂ����B������f�͗U�d�̂̎�ނɂ���Č��܂�1��菬���Ȑ��̒萔�ł���B�U�d���ɂɂ���ėU�d�̂̉��̖ʂɔ��������������̖ʓd�ׂɂ��āA�P�ʖʐϓ�����̓d�C�ʂ������B����ɁA�ɔ��R���f���T�[�Ƃ��čl�����Ƃ��̓d�C�e�ʂ������B
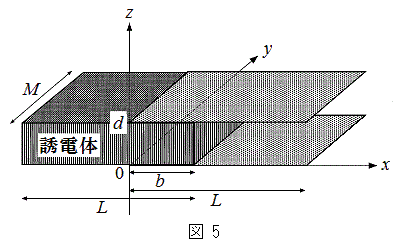 ��8�@��7�̏�Ԃ���U�d�̂��I�Ɉ��������A�}5�̂悤�ɁAx�������ɐ[��
��8�@��7�̏�Ԃ���U�d�̂��I�Ɉ��������A�}5�̂悤�ɁAx�������ɐ[��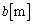 (
(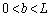 )�܂ő}��������ԂƂ����B�U�d�̂��}������Ă���̈�Ƒ}������Ă��Ȃ��̈�ɂ����鉺�̋ɔ�(
)�܂ő}��������ԂƂ����B�U�d�̂��}������Ă���̈�Ƒ}������Ă��Ȃ��̈�ɂ����鉺�̋ɔ�(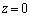 )�̖ʓd�ׂɂ��āA�P�ʖʐϓ�����̓d�C�ʂ����ꂼ�ꎦ���B
)�̖ʓd�ׂɂ��āA�P�ʖʐϓ�����̓d�C�ʂ����ꂼ�ꎦ���B��9�@��8�̏�Ԃɂ����āA��̋ɔ̊Ԃ̓d�ʍ��̑傫���ƁA�R���f���T�[�Ƃ��Ē~�����Ă���Ód�G�l���M�[�������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�u�U�d�̂�}������R���f���T�[�v�Ƃ�����ގ��͕̂p�o�̂��̂ł����A�����̍l�������@�B�I�ɂ��Ă͂߂邱�Ƃ��ł��Ȃ��悤�ɍH�v����Ă��āA�l���Â炢���ł��B���ɖ�8�́A��6�A��7�����܂����p����K�v������܂��B
�T�D��1�@�d��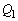 ����
����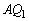 �{���d�C�͐����������܂��BO�𒆐S�Ƃ������ar�̋��ʂ��ʐ���
�{���d�C�͐����������܂��BO�𒆐S�Ƃ������ar�̋��ʂ��ʐ���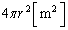 �ł��B�_�d��
�ł��B�_�d��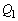 ��O�ɒu���Ƃ��AO��������
��O�ɒu���Ƃ��AO��������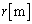 �̓_�ɂ����āA�P�ʖʐ���������d�C�͐��̖{���́A
�̓_�ɂ����āA�P�ʖʐ���������d�C�͐��̖{���́A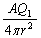
�d���x�N�g���̓��a���������́A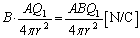 ......[��]
......[��]
��2�@��1�̌��ʂ��A�d��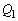 ���_P�ɍ���d���́A�傫��
���_P�ɍ���d���́A�傫��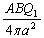 �ŁA�����͓��a�����������ł��B
�ŁA�����͓��a�����������ł��B �d��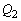 ���_P�ɍ���d���́A�傫��
���_P�ɍ���d���́A�傫��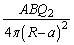 �ŁA�����́A�}2(a)��
�ŁA�����́A�}2(a)��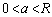 �̏ꍇ�ɂ͓��a�����������A�}2(b)��
�̏ꍇ�ɂ͓��a�����������A�}2(b)��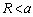 �̏ꍇ�ɂ͓��a�����������ł��B
�̏ꍇ�ɂ͓��a�����������ł��B
�d�ˍ��킹�̌������A�_P�ɂ������d���̓��a���������́A
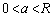 �̏ꍇ�ɂ́A
�̏ꍇ�ɂ́A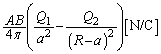 ......[��]
......[��]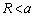 �̏ꍇ�ɂ́A
�̏ꍇ�ɂ́A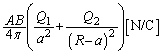 ......[��]
......[��]
�U�D��3�@�����ʐ���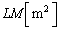 �ŁA���ɕ��z�����ʓd�������d�C����
�ŁA���ɕ��z�����ʓd�������d�C����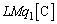 �C�����ʓd�����甭�������d�C�͐��̑��{����
�C�����ʓd�����甭�������d�C�͐��̑��{����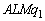 �{�C�����҂�����ƕ����Ȗʂ��l����ƁA�����ʐ���
�{�C�����҂�����ƕ����Ȗʂ��l����ƁA�����ʐ���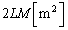 �C�P�ʖʐ���������d�C�͐��̖{����
�C�P�ʖʐ���������d�C�͐��̖{����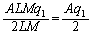 �C�d���̑傫���́A
�C�d���̑傫���́A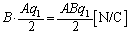 �C�����́A
�C�����́A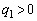 �̏ꍇ�A������o�čs�������ŁA
�̏ꍇ�A������o�čs�������ŁA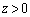 �̕����ł�z���������ł�(�K�E�X�̖@�����Q��)�B
�̕����ł�z���������ł�(�K�E�X�̖@�����Q��)�B �ʓd���ɂ��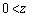 �ł��d����z�����������́A
�ł��d����z�����������́A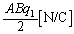 ......[��]�d���̌�����
......[��]�d���̌�����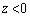 �̕����ł�z���������ŁA
�̕����ł�z���������ŁA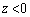 �ł��d����z�����������́A
�ł��d����z�����������́A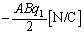 �ł��B
�ł��B ��4�@��3�Ɠ��l�ɁA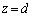 �Ɉʒu�����ʓd���̍���d����z�����������́A
�Ɉʒu�����ʓd���̍���d����z�����������́A 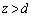 �ɂ����āA
�ɂ����āA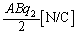 �C
�C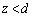 �ɂ����āA
�ɂ����āA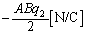
�d�ˍ��킹�̌������A���ʓd���̍���d����z�����������́A
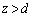 �ɂ����āA
�ɂ����āA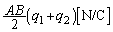 ......[��]
......[��]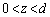 �ɂ����āA
�ɂ����āA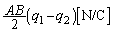 ......[��]
......[��]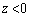 �ɂ����āA
�ɂ����āA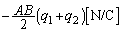 ......[��]
......[��]
�V�D��5�@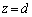 �Ɉʒu�����ʓd�������d�C����
�Ɉʒu�����ʓd�������d�C����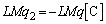 �ł����A�����ʓd�����A
�ł����A�����ʓd�����A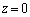 �Ɉʒu�����ʓd���ɂ��
�Ɉʒu�����ʓd���ɂ��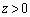 �̕����ɍ�����d��
�̕����ɍ�����d��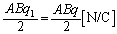 ������d�C���́A
������d�C���́A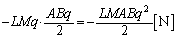 (�}�C�i�X��z�������������ł��邱�Ƃ��Ӗ����܂�)
(�}�C�i�X��z�������������ł��邱�Ƃ��Ӗ����܂�) ���ɔ��L����̂ɕK�v���G�l���M�[�A�����A�����d�C���ɋt�炤z�����������O��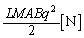 ���ʓd��������d�����ړ�������Ƃ��ɂ����d���́A
���ʓd��������d�����ړ�������Ƃ��ɂ����d���́A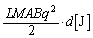 ......[��]
......[��] ��6�@��4�̌��ʂ��A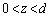 �ɂ������d���͈�l�ŁA
�ɂ������d���͈�l�ŁA 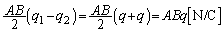 �@����@
�@����@�����F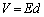 (�d�ʁE�d�����Q��)���A�ɔԂ��d�ʍ��̑傫��V�́A
(�d�ʁE�d�����Q��)���A�ɔԂ��d�ʍ��̑傫��V�́A 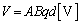 ......[��]
......[��]���D����d�̋ɔԂ��d�ʍ����A�P�ʖʐ���������d�C��q��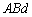 �����������̂ɂȂ邱�Ƃɒ��ӂ��Ă��������B
�����������̂ɂȂ邱�Ƃɒ��ӂ��Ă��������B �R���f���T�[�ɒ~����ꂽ�d����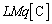 �ŁA�����F
�ŁA�����F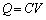 (�R���f���T�[���Q��)���A�R���f���T�[���Ód�e���́A
(�R���f���T�[���Q��)���A�R���f���T�[���Ód�e���́A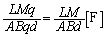 ......[��]
......[��]
�W�D��7�@�U�d�̂�}��������̋ɔԂ��d�ʍ�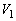 �́A��6�̌��ʂ�f�{����(�U�d�������Q��)�A
�́A��6�̌��ʂ�f�{����(�U�d�������Q��)�A ���D�ɔԂɗU�d�̂�}������ƁA����d�̋ɔԂ��d�ʍ��́A�P�ʖʐ���������d�C��q��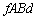 �����������̂ɂȂ邱�Ƃɒ��ӂ��Ă��������B
�����������̂ɂȂ邱�Ƃɒ��ӂ��Ă��������B �ɔԂ��d���̑傫��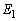 �́A�����F
�́A�����F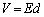 ���A
���A �ɔԂɂ́A�d�C�͐����P�ʖʐ�������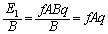 �{�A�������Ă��܂��B
�{�A�������Ă��܂��B
�@���A�ɔԂɂ́A���Ƃ��ƁA�傫��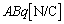 ���d��������A�P�ʖʐ�������
���d��������A�P�ʖʐ�������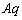 �{���d�C�͐����������Ă��܂����B
�{���d�C�͐����������Ă��܂����B
�U�d�̂̑}���ɂ��A�ɔԂ�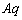 �{�������d�C�͐���
�{�������d�C�͐���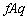 �{�Ɍ������A�Ƃ������Ƃ́A�U�d�̂̏�Ɖ��̖ʂɌ��������ʓd�����������āA
�{�Ɍ������A�Ƃ������Ƃ́A�U�d�̂̏�Ɖ��̖ʂɌ��������ʓd�����������āA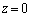 �C
�C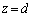 ���ʓd�����甭�������d�C�͐��̈ꕔ
���ʓd�����甭�������d�C�͐��̈ꕔ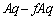 �{���A���������ʓd���ɏI�[���Ă��܂����A�Ƃ������Ƃ��Ӗ����Ă��܂��B
�{���A���������ʓd���ɏI�[���Ă��܂����A�Ƃ������Ƃ��Ӗ����Ă��܂��B
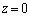 ���ʓd���ƑΌ�����U�d�̂̕\�ʁA�܂�A�U�d�̂̉��̖ʂɂ́A
���ʓd���ƑΌ�����U�d�̂̕\�ʁA�܂�A�U�d�̂̉��̖ʂɂ́A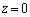 �Ƃ͋t�ɐ����d��(���d��)���������A���̖ʂɔ����������������ʓd�����P�ʖʐ���������d�C���́A
�Ƃ͋t�ɐ����d��(���d��)���������A���̖ʂɔ����������������ʓd�����P�ʖʐ���������d�C���́A 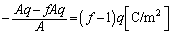 ......[��]
......[��]�R���f���T�[�ɒ~�����Ă����d����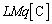 �̂܂܂ŁA�����F
�̂܂܂ŁA�����F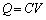 ���A�Ód�e���́A
���A�Ód�e���́A 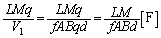 ......[��]
......[��]��8�@�U�d�̂��}������Ă��镔�����ʐ���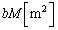 �ŁA��7�Ɠ��l�ɁA�Ód�e����
�ŁA��7�Ɠ��l�ɁA�Ód�e����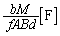
�U�d�̂��}������Ă��Ȃ��������ʐ���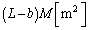 �ŁA�Ód�e����
�ŁA�Ód�e����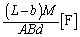 2�̃R���f���T�[�͕���ڑ�����Ă��āA�����e���́A
2�̃R���f���T�[�͕���ڑ�����Ă��āA�����e���́A �R���f���T�[�ɒ~�����Ă����d����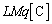 �̂܂܂ŁA�����F
�̂܂܂ŁA�����F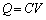 ���A�ɔԂ��d�ʍ�
���A�ɔԂ��d�ʍ�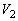 �́A
�́A 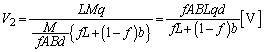 �@����A
�@����A��7�̒��D�𗘗p���āA�U�d�̂��}������Ă���̈���P�ʖʐ���������d�C���́A
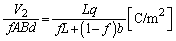 ......[��]
......[��]��6�̒��D�𗘗p���āA�U�d�̂��}������Ă��Ȃ��̈���P�ʖʐ���������d�C���́A
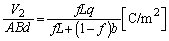 ......[��]
......[��]��9�@�A���A�ɔԂ��d�ʍ��̑傫���́A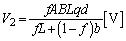 ......[��]
......[��] 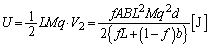 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 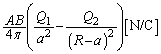 ......[��]
......[��]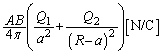 ......[��]
......[��]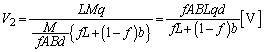 �@����A
�@����A