�É��啨��'10�N[2]
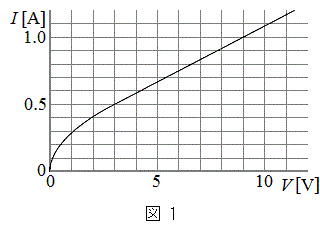 �d���Ɠd���̊W���}1�ŕ\�����悤�ȓd��������B�����ŁA�d��
�d���Ɠd���̊W���}1�ŕ\�����悤�ȓd��������B�����ŁA�d��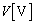 �Ɠd��
�Ɠd��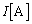 �̊Ԃ̊W���́A
�̊Ԃ̊W���́A
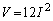 (
(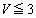 )�C
)�C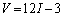 (
(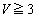 )
)
�ƕ\����A�܂��A�d���̖��邳�͂��̏���d�͂ɔ�Ⴗ����̂Ƃ���B���̓d���ƁA�N�d��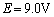 �C������R
�C������R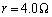 �̓d�r��p���ĉ�H��������B�ȉ��̖₢�ɓ�����B�������A���l�͗L������2���œ�����B
�̓d�r��p���ĉ�H��������B�ȉ��̖₢�ɓ�����B�������A���l�͗L������2���œ�����B
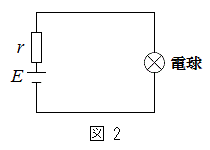 ��1�@�}2�̂悤�ɁA���̓d����d�r1�ɂȂ����Ƃ��A�d���ɗ����d��
��1�@�}2�̂悤�ɁA���̓d����d�r1�ɂȂ����Ƃ��A�d���ɗ����d��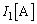 �����߂�B
�����߂�B
 ��2�@�}3�̂悤�ɁA�d�r2�����ɂȂ��œd���Ƃ��A����ɓd�����Ȃ����B���̂Ƃ��A�d���ɗ����d��
��2�@�}3�̂悤�ɁA�d�r2�����ɂȂ��œd���Ƃ��A����ɓd�����Ȃ����B���̂Ƃ��A�d���ɗ����d��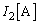 �����߂�B
�����߂�B
��3�@�u�d���Ɠd���̊W���}1�ŕ\�����悤�ȓd���̏ꍇ�A2�̓d���̖��邳�������Ƃ��A�d���̓d���A�d���͂��ꂼ�ꓙ�����v���Ƃ��������B
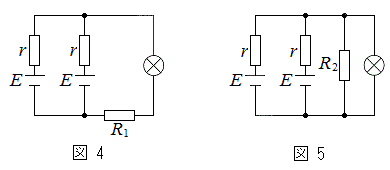 ��4�@�}3�̉�H�ɂ��āA�V���ɒ�R���Ȃ��Ő}2�̓d�r1�̏ꍇ�Ɠ������邳�ɂȂ�悤�ɂ����B
��4�@�}3�̉�H�ɂ��āA�V���ɒ�R���Ȃ��Ő}2�̓d�r1�̏ꍇ�Ɠ������邳�ɂȂ�悤�ɂ����B(1) �}4�̂悤�ɒ�R���Ȃ����Ƃ��A��R�̑傫��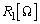 �����߂�B
�����߂�B (2) �}5�̂悤�ɒ�R���Ȃ����Ƃ��A��R�̑傫��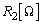 �����߂�B
�����߂�B
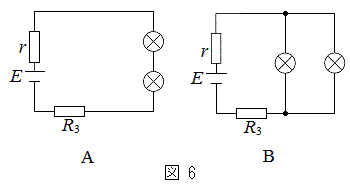 ��5�@���̓d��2�Ɠd�r1�A����ђ�R��p���āA�}6�̂悤��2�ʂ�̉�HA��B��������B��HA�Ɖ�HB�̓d���̖��邳�������Ƃ��A��R�̑傫��
��5�@���̓d��2�Ɠd�r1�A����ђ�R��p���āA�}6�̂悤��2�ʂ�̉�HA��B��������B��HA�Ɖ�HB�̓d���̖��邳�������Ƃ��A��R�̑傫��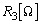 �����߂�B�������A�r���o�߂�������Ȃ���L�q���邱�ƁB
�����߂�B�������A�r���o�߂�������Ȃ���L�q���邱�ƁB
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�d�r�����`��R������ɂȂ��������ɂȂ����肷��̂ŁA������̂��낤���A�ƁA�v���Ă��܂��܂����A�{��ł́A������悤�ɂ��܂��H�v����Ă��܂��B
�}1�ɂ����āA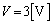 �̂Ƃ��A�^����ꂽ�W�����A
�̂Ƃ��A�^����ꂽ�W�����A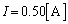 �ł��B
�ł��B
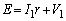
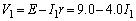 �@����@
�@����@�� 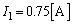 ......[��]�@(
......[��]�@(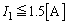 ����)�@���A���̂Ƃ�
����)�@���A���̂Ƃ�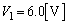 �ł��B
�ł��B ���ӁD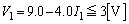 �Ƃ���ƁA
�Ƃ���ƁA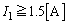
���̂Ƃ��́A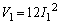 ���A
���A
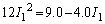
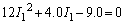
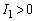 ���
���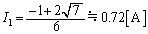 �ƂȂ�܂����A
�ƂȂ�܂����A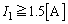 �����Ȃ��̂ŕs�K�ł��B
�����Ȃ��̂ŕs�K�ł��B
�܂��A�@�̃O���t��}1�ɏ�������Ō�_��V��I�̒l��ǂނ��Ƃɂ���Ă��ł��܂��B�����ł́A���炩���߁A�O���t���炨�悻�̒l��m���āA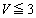 �̂Ƃ��̎��A
�̂Ƃ��̎��A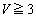 �̂Ƃ��̎���I��ŁA������p���ĉ���̂��悢�ł��傤�B
�̂Ƃ��̎���I��ŁA������p���ĉ���̂��悢�ł��傤�B
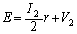
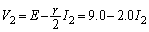 �@����A
�@����A�� 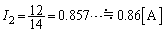
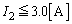 �����̂ŁA
�����̂ŁA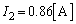 ......[��]�A���A���̂Ƃ�
......[��]�A���A���̂Ƃ�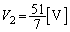 �ł��B
�ł��B
���ӁD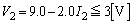 �Ƃ���ƁA
�Ƃ���ƁA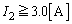
���̂Ƃ��́A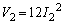 ���A
���A 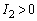 ���
���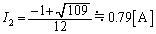 �ƂȂ�܂����A
�ƂȂ�܂����A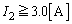 �����Ȃ��̂ŕs�K�ł��B
�����Ȃ��̂ŕs�K�ł��B
�܂��A�A�̃O���t��}2�ɏ�������Ō�_��V��I�̒l��ǂނ��Ƃɂ���Ă��ł��܂��B
��3�@2�̓d���̖��邳���������Ƃ�����d��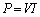 ���������Ȃ�܂��B
���������Ȃ�܂��B 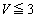 (
(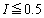 )�̂Ƃ��A
)�̂Ƃ��A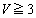 (
(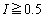 )�̂Ƃ�
)�̂Ƃ�����d��P�́A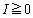 �ɂ����āAI���P���������Ȃ̂ŁA����d��P����������A�d�����d��I���������A����ɁA�d�����d��V���������Ȃ�܂��B
�ɂ����āAI���P���������Ȃ̂ŁA����d��P����������A�d�����d��I���������A����ɁA�d�����d��V���������Ȃ�܂��B
��4�@��3���A�d�����d����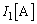 �C�d����
�C�d����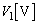 �ł��B
�ł��B �� 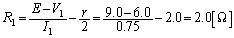 ......[��]
......[��] �� 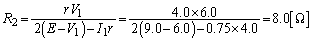 ......[��]
......[��]
��5�@��3���A��B�œd�����d�����d���͓����l�ɂȂ�܂��B�d�����d����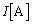 �C�d����
�C�d����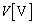 �Ƃ��܂��B
�Ƃ��܂��B A�ł́A��R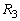 �C�܂��A������R�ɗ�����d����
�C�܂��A������R�ɗ�����d����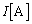 �ł��B�L���q�z�b�t��2�@��
�ł��B�L���q�z�b�t��2�@�����A
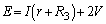 �@����B
�@����BB�ł́A��R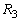 �C�܂��A������R�ɗ�����d����
�C�܂��A������R�ɗ�����d����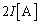 �ł��B�L���q�z�b�t��2�@��
�ł��B�L���q�z�b�t��2�@�����A
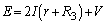 �@����C
�@����C�B�~2�|�C���A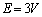
�� 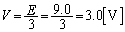 ���̂Ƃ��A�^����ꂽ�W�����
���̂Ƃ��A�^����ꂽ�W�����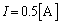
�B���A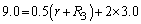
�� 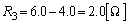 ......[��]
......[��]
�NjL�D���������Ȃ̂ŁA��5��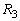 �̒l���^�����Ă��āA�d�����d�����d�������߂邱�Ƃ��l���Ă݂܂��B
�̒l���^�����Ă��āA�d�����d�����d�������߂邱�Ƃ��l���Ă݂܂��B ��5��A�ŁA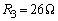 ���Ƃ��܂��B�B�́A
���Ƃ��܂��B�B�́A �ɂȂ�܂��B���̃O���t��}1�ɏ�������ŁA��_��V��I��ǂ߂A�d�����d�����d�������߂邱�Ƃ��ł��܂��B
�����ł��̂Ȃ�A���̂Ƃ��́A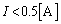 �C
�C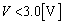 �Ȃ̂ŁA
�Ȃ̂ŁA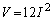 �Ƃ��āA
�Ƃ��āA 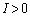 ���
���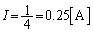 �C
�C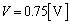
��5��B�ŁA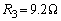 ���Ƃ��܂��B�C�́A
���Ƃ��܂��B�C�́A�ɂȂ�܂��B���̃O���t��}1�ɏ�������ŁA��_��V��I��ǂ߂A�d�����d�����d�������߂邱�Ƃ��ł��܂��B
���̏ꍇ���A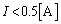 �C
�C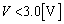 �Ȃ̂ŁA
�Ȃ̂ŁA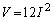 �Ƃ��āA
�Ƃ��āA 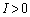 ���
���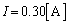 �C
�C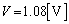
����`��R����������ɂȂ��Ă��Ă��A1�̂Ƃ��Ɠ��l�ɉł��邱�Ƃ��o���Ă����Ă��������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B