京大物理'13年[2]
次の文章を読んで、 に適した式か値を、それぞれの解答欄に記入せよ。問1,問2については、指示にしたがって、解答をそれぞれの解答欄に記入せよ。
なお、以下の設問では、極板等はすべて真空中にあり、真空の誘電率を とする。コンデンサーの極板は極板間距離に比べて十分大きく、極板端での電場の乱れは無視できる。導線や導体の抵抗は無視できるものとし、導線はしなやかで軽く、質量が無視できるとともに、極板の動きに影響を与えないものとする。また、重力加速度をgとする。
とする。コンデンサーの極板は極板間距離に比べて十分大きく、極板端での電場の乱れは無視できる。導線や導体の抵抗は無視できるものとし、導線はしなやかで軽く、質量が無視できるとともに、極板の動きに影響を与えないものとする。また、重力加速度をgとする。
 (1) 図1のように、極板①と極板②からなる平行板コンデンサーがある。極板①は固定されており、極板②は左右に滑らかに動かすことができる。コンデンサーの極板の面積をSとし、極板①には電荷
(1) 図1のように、極板①と極板②からなる平行板コンデンサーがある。極板①は固定されており、極板②は左右に滑らかに動かすことができる。コンデンサーの極板の面積をSとし、極板①には電荷 が、極板②には電荷
が、極板②には電荷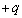 が蓄えられているものとする(
が蓄えられているものとする(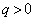 )。
)。極板①に垂直で極板②に向かう方向をx軸とし、極板①の位置を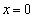 ,極板②の位置を
,極板②の位置を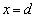 とする(
とする(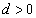 )。このとき、コンデンサーに蓄えられているエネルギーWは イ である。ここで、極板②を平行に保ったまま微小距離
)。このとき、コンデンサーに蓄えられているエネルギーWは イ である。ここで、極板②を平行に保ったまま微小距離 だけ極板①と反対方向に動かしたあとにコンデンサーに蓄えられているエネルギー
だけ極板①と反対方向に動かしたあとにコンデンサーに蓄えられているエネルギー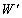 は ロ である。このエネルギーの変化
は ロ である。このエネルギーの変化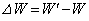 は、極板①と極板②が引き合う力に逆らって動かしたために生じたものである。そこで、このエネルギーの変化から極板②に働く力
は、極板①と極板②が引き合う力に逆らって動かしたために生じたものである。そこで、このエネルギーの変化から極板②に働く力 の大きさを求めると、 ハ となる。
の大きさを求めると、 ハ となる。
 (2) 図2のように、極板③と極板④、および極板⑤と極板⑥からなる2つの平行板コンデンサーがある。極板③は固定されている。極板④と極板⑤は質量が無視できる導体の棒で接続されて一体化しており、極板を平行に保ったまま上下に滑らかに動かすことができるものとする。図2のように2つのコンデンサーは直列に接続されており、電圧Vがかかっている。これら2つのコンデンサーは十分離れており、互いにクーロン力を及ぼさない。極板③と極板④の面積はともに
(2) 図2のように、極板③と極板④、および極板⑤と極板⑥からなる2つの平行板コンデンサーがある。極板③は固定されている。極板④と極板⑤は質量が無視できる導体の棒で接続されて一体化しており、極板を平行に保ったまま上下に滑らかに動かすことができるものとする。図2のように2つのコンデンサーは直列に接続されており、電圧Vがかかっている。これら2つのコンデンサーは十分離れており、互いにクーロン力を及ぼさない。極板③と極板④の面積はともに ,極板⑤と極板⑥の面積はともに
,極板⑤と極板⑥の面積はともに ,それぞれの極板の質量は面積に比例し、その比例定数をpとする(
,それぞれの極板の質量は面積に比例し、その比例定数をpとする(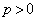 )。2つのコンデンサーの極板間距離をともにdとする。このとき、極板③と極板④が引き合う力の大きさは ニ である。
)。2つのコンデンサーの極板間距離をともにdとする。このとき、極板③と極板④が引き合う力の大きさは ニ である。いま、極板が引き合う力と重力がつり合うように電圧Vを調整すると、2つのコンデンサーの極板間距離がともにdとなった状態で静止した。このとき、極板の面積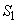 は
は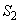 の ホ 倍であり、電圧Vは、極板の面積
の ホ 倍であり、電圧Vは、極板の面積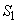 ,
, を用いることなく ヘ と表すことができる。
を用いることなく ヘ と表すことができる。
 (3) 図3のように、極板⑦と極板⑧,および極板⑨と極板⑩からなる2つの平行板コンデンサーがある。極板⑦と極板⑩は固定されている。極板⑧と極板⑨は質量が無視できる絶縁体のバネで接続されており、極板を平行に保ったまま上下に滑らかに動かすことができるものとする。このバネのバネ定数はkである。2つのコンデンサーは十分離れており、互いにクーロン力を及ぼさない。すべての極板の面積はSであり、質量を
(3) 図3のように、極板⑦と極板⑧,および極板⑨と極板⑩からなる2つの平行板コンデンサーがある。極板⑦と極板⑩は固定されている。極板⑧と極板⑨は質量が無視できる絶縁体のバネで接続されており、極板を平行に保ったまま上下に滑らかに動かすことができるものとする。このバネのバネ定数はkである。2つのコンデンサーは十分離れており、互いにクーロン力を及ぼさない。すべての極板の面積はSであり、質量を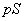 とする(
とする(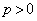 )。
)。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 (ホ)(へ)あたりの計算の巧拙が勝負の分かれ目です。(3)問1の問題文がうまくないので、かなり悩みますが、極板⑨に働く重力も考慮に入れるようにしてください。
(イ)  ......[答]極板②を動かしたあとの静電容量は
......[答]極板②を動かしたあとの静電容量は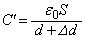 ,静電エネルギー
,静電エネルギー は、
は、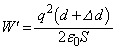 (ロ)
(ロ) 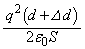 ......[答]
......[答] ∴ 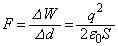
(ハ)  ......[答]
......[答]
(2) 極板③と極板④の間のコンデンサーの静電容量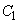 は、
は、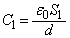 ,極板⑤と極板⑥の間のコンデンサーの静電容量
,極板⑤と極板⑥の間のコンデンサーの静電容量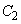 は、
は、 ,
,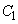 ,
, 直列接続の合成容量
直列接続の合成容量 は、
は、 極板③,④,⑤,⑥に蓄えられる電気量の大きさは、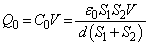 (ハ)の結果を用いて、極板③と極板④が引き合う力の大きさは、
(ハ)の結果を用いて、極板③と極板④が引き合う力の大きさは、 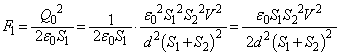 ・・・(a)
・・・(a)(ニ) 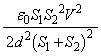 ......[答]同様に、
......[答]同様に、 ・・・(b)一体化している極板④と極板⑤が受ける力は、上向きのクーロン力
・・・(b)一体化している極板④と極板⑤が受ける力は、上向きのクーロン力 ,下向きのクーロン力
,下向きのクーロン力 ,極板④と極板⑤が受ける重力
,極板④と極板⑤が受ける重力 ,これらのつり合いより、
,これらのつり合いより、 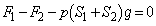 ・・・(c)
・・・(c)極板⑥が受ける力は、上向きのクーロン力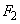 ,下向きの重力
,下向きの重力 ,これらのつり合いより、
,これらのつり合いより、 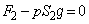 ∴
∴ 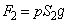 ・・・(d)
・・・(d)(a)÷(b)より、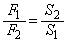 (d)より、
(d)より、 (c)より、
(c)より、
∴  ,
, (ホ)
(ホ) 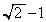 ......[答]この結果と、(b),(d)より、
......[答]この結果と、(b),(d)より、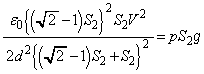
∴ 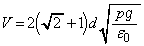
(ヘ) 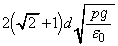 ......[答]
......[答]
(3) このとき、極板⑦と極板⑧の間に働くクーロン力は、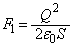 ,極板⑨と極板⑩の間に働くクーロン力は、
,極板⑨と極板⑩の間に働くクーロン力は、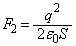 となります。
となります。 極板⑨に働く力は、バネの自然長からの伸びをxとして、上向きの弾性力 ,下向きのクーロン力
,下向きのクーロン力 ,下向きの重力
,下向きの重力 です。これらの力のつり合いより、
です。これらの力のつり合いより、 ∴ 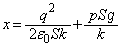 (
(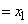 とします)
とします)
(ト)  ......[答]時刻
......[答]時刻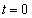 でスイッチを閉じると、極板⑨と極板⑩の間に働くクーロン力がなくなり、極板⑧が静止したままなので、静止していた極板⑨はこのときの位置を振動端として単振動を始めます。単振動の中心は、
でスイッチを閉じると、極板⑨と極板⑩の間に働くクーロン力がなくなり、極板⑧が静止したままなので、静止していた極板⑨はこのときの位置を振動端として単振動を始めます。単振動の中心は、 がなくなったときの、極板⑨に働く力のつり合いの位置(
がなくなったときの、極板⑨に働く力のつり合いの位置( とします)です。
とします)です。 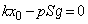 ∴
∴ 
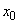 は最初の位置から、
は最初の位置から、だけ上方にあります。
(チ)  ......[答](チ)の結果は、振動端と振動中心の間の距離、つまり、単振動の振幅です。(リ)
......[答](チ)の結果は、振動端と振動中心の間の距離、つまり、単振動の振幅です。(リ) 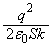 ......[答]
......[答]
極板⑨の加速度をaとして、極板⑨の運動方程式は、 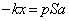 ∴
∴ 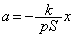
よって極板⑨の単振動の角振動数は、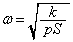
単振動の周期は、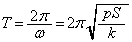 (ヌ)
(ヌ)  ......[答]
......[答] 問1 極板⑧に働く力は、上向きのクーロン力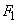 ,下向きの弾性力
,下向きの弾性力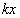 ,下向きの重力
,下向きの重力 です。極板⑧が静止しているなら、これらの間に力のつり合いが成立するはずで、
です。極板⑧が静止しているなら、これらの間に力のつり合いが成立するはずで、 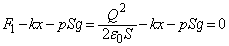 ・・・(e)
・・・(e)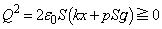
これより、 であれば制御可能です。
であれば制御可能です。
単振動は、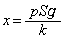 を振動中心とし、振幅が
を振動中心とし、振幅が なので、
なので、 この範囲のxの値に対して制御可能であるために、
∴ 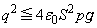 ∴
∴  ......[答]
......[答] 問2 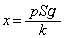 が振動中心で、振幅が
が振動中心で、振幅が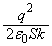 ,
, において、
において、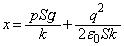 であったことから、
であったことから、 (e)より、
∴ 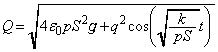 ......[答]
......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
京大物理TOP 物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 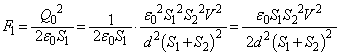 ・・・(a)
・・・(a)
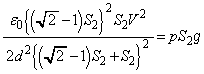
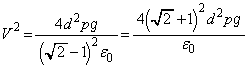
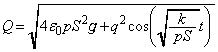 ......[答]
......[答]