���啨��'22�N�O��[3]
���̕��͂�ǂ�ŁA�@�@�@�ɓK�������܂��͐��l���A{�@�@�@}����͓K�Ȃ��̂����ׂđI�т��̔ԍ����A���ꂼ��̉��ɋL������B��1�C��2�ł́A�w���ɂ��������āA�����ꂼ��̉��ɋL������B�������A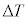 �Ȃ�
�Ȃ�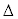 ��t���������ʂ͔����ʂł���A1���̍��܂ł��l������̂Ƃ���B
��t���������ʂ͔����ʂł���A1���̍��܂ł��l������̂Ƃ���B
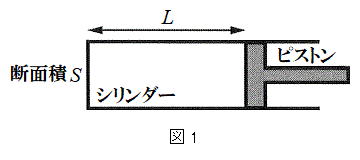 (1) �}1�̂悤�ɁA�s�X�g���ɂ���āA�f�ʐ�S�̃V�����_�[���ɖ����ꂽ����(mol)��n�̗��z�C�̂��l����B�ȉ��A�V�����_�[���̗��z�C�̂�P�ɋC�̂ƌĂԁB�V�����_�[�͌Œ肳��Ă���A�s�X�g���͖��C�Ȃ��ɓ������̂Ƃ���B�����ŁA�C�̒萔��R�Ƃ���B�V�����_�[�̒�(���[)�ƃs�X�g���̓��ʂƂ̊Ԃ̒�����L�C�C�̂̐�Ή��x��T�Ƃ���B���̂Ƃ��A�V�����_�[���̋C�̂̈���p�́A
(1) �}1�̂悤�ɁA�s�X�g���ɂ���āA�f�ʐ�S�̃V�����_�[���ɖ����ꂽ����(mol)��n�̗��z�C�̂��l����B�ȉ��A�V�����_�[���̗��z�C�̂�P�ɋC�̂ƌĂԁB�V�����_�[�͌Œ肳��Ă���A�s�X�g���͖��C�Ȃ��ɓ������̂Ƃ���B�����ŁA�C�̒萔��R�Ƃ���B�V�����_�[�̒�(���[)�ƃs�X�g���̓��ʂƂ̊Ԃ̒�����L�C�C�̂̐�Ή��x��T�Ƃ���B���̂Ƃ��A�V�����_�[���̋C�̂̈���p�́A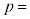 �@���@�ł���B
�@���@�ł���B�}1�̏�Ԃ���A����2�ʂ�̏�ԕω��ɂ��čl����B
�A) �C�̂̑̐ς����ɕۂ��ĊO������M�������A���x��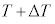 �Ƃ����B�C�͎̂d�������Ȃ��̂ŁA���̔M�͂��ׂē����G�l���M�[�ɕω�����B���̂Ƃ��A��σ�����M��
�Ƃ����B�C�͎̂d�������Ȃ��̂ŁA���̔M�͂��ׂē����G�l���M�[�ɕω�����B���̂Ƃ��A��σ�����M��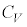 �Ƃ���ƁA�C�̂̓����G�l���M�[�̕ω�
�Ƃ���ƁA�C�̂̓����G�l���M�[�̕ω�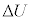 �Ɖ��x�̕ω�
�Ɖ��x�̕ω�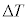 �̊Ԃɂ́A
�̊Ԃɂ́A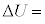 �@���@�Ƃ����W�������藧�B
�@���@�Ƃ����W�������藧�B �C) �C�̂̉��xT�����ɕۂ��ăs�X�g���������A������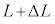 �Ƃ����B���̂Ƃ��A�����G�l���M�[�̕ω���
�Ƃ����B���̂Ƃ��A�����G�l���M�[�̕ω���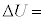 �@���@�ł���A�C�̂��O���ɂ����d��
�@���@�ł���A�C�̂��O���ɂ����d��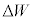 �́A
�́A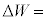 �@���@
�@���@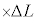 �ƂȂ�B
�ƂȂ�B 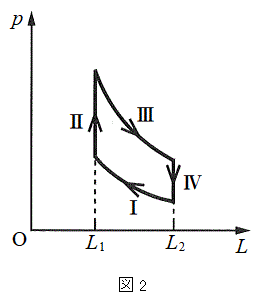 �O�q�̂悤�ȋC�̂̏�ԕω���g�ݍ��킹�āA�}2�̂悤�ȁA�ߒ��T�C�ߒ��U�C�ߒ��V�C�ߒ��W��4�̉ߒ�����Ȃ�M�͊w�I�ȃT�C�N�����l����B
�O�q�̂悤�ȋC�̂̏�ԕω���g�ݍ��킹�āA�}2�̂悤�ȁA�ߒ��T�C�ߒ��U�C�ߒ��V�C�ߒ��W��4�̉ߒ�����Ȃ�M�͊w�I�ȃT�C�N�����l����B
�E�@�ߒ��T�ł́A���x��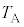 �ɕۂ����܂܁A������
�ɕۂ����܂܁A������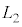 ����
����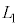 �ɂȂ�܂ŁA�������s�X�g���������B
�ɂȂ�܂ŁA�������s�X�g���������B �E�@�ߒ��U�ł́A����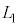 �̂܂܁A���x��
�̂܂܁A���x��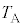 ����
����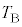 �ɏ㏸������B
�ɏ㏸������B �E�@�ߒ��V�ł́A���x��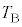 �ɕۂ����܂܁A������
�ɕۂ����܂܁A������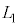 ����
����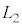 �ɂȂ�܂ŁA�������s�X�g���������B
�ɂȂ�܂ŁA�������s�X�g���������B �E�@�ߒ��W�ł́A����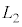 �̂܂܁A���x��
�̂܂܁A���x��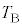 ����
����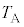 �ɖ߂��B
�ɖ߂��B �Ȃ��A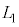 �C
�C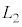 �C
�C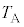 �C
�C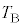 �́A���鐳�̒萔�ł���A
�́A���鐳�̒萔�ł���A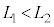 �C
�C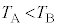 �����B
�����B
�����̉ߒ��̂����A�C�̂��z�M����ߒ������ׂċ�����ƁA{���F�@�ߒ��T�C�A�ߒ��U�C�B�ߒ��V�C�C�ߒ��C}���Y������B���̃T�C�N���ɂ����āA�C�̂��O���ɑ��Ă���d���̑��ʂ́A{���F�@���C�A0�C�B��}�ł���B
(2) ���z�C�̂Ƃ͈قȂ镨����p���Ă��A�M�͊w�I�ȃT�C�N������邱�Ƃ��ł���B�ȉ��ł́A�S���̂悤�ɐL�k����q����M�͊w�I�ɍl�@���Ă݂悤�B�q�������R��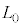 ��������L���ƁA���̒��͂́A�����������Ƌt�����ɍ�p����B�q���̒��͂̑傫��F���A��Ή��xT�Ɉˑ����A����L (
��������L���ƁA���̒��͂́A�����������Ƌt�����ɍ�p����B�q���̒��͂̑傫��F���A��Ή��xT�Ɉˑ����A����L (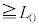 )�̂Ƃ��A
)�̂Ƃ��A �ŕ\�����ꍇ���l����B�����ŁA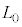 �ƌW��A�́A�������T��L�ɂ��Ȃ����̒萔�Ƃ���B�܂��A���̃q���̓����G�l���M�[U�͐�Ή��xT�ɔ�Ⴕ�AL�ɂ��Ȃ����̌W��K��p����
�ƌW��A�́A�������T��L�ɂ��Ȃ����̒萔�Ƃ���B�܂��A���̃q���̓����G�l���M�[U�͐�Ή��xT�ɔ�Ⴕ�AL�ɂ��Ȃ����̌W��K��p���� �ƕ\������̂Ƃ���B
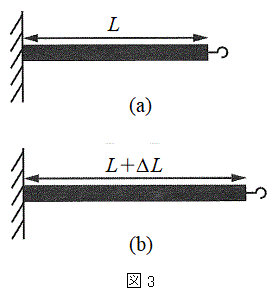 �}3(a)�̂悤�ȁA����L (
�}3(a)�̂悤�ȁA����L (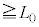 )�C���xT�̃q�����A
)�C���xT�̃q�����A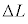 ��������ɐL���A�}3(b)�̂悤�ɒ���
��������ɐL���A�}3(b)�̂悤�ɒ���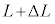 �C���x
�C���x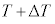 �ɂȂ����Ƃ���B���̉ߒ��ŁA�q�����O���ɂ����d���́A�q���̒���F��p����
�ɂȂ����Ƃ���B���̉ߒ��ŁA�q�����O���ɂ����d���́A�q���̒���F��p���� �Ə�����B�q���̋z�M�ʂ�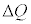 �Ƃ���ƁA�q���̓����G�l���M�[�̕ω�
�Ƃ���ƁA�q���̓����G�l���M�[�̕ω�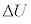 �́AF�CK�C
�́AF�CK�C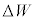 ��p�����ɕ\���ƁA
��p�����ɕ\���ƁA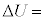 �@���@�ƂȂ�B����A���̉ߒ��ɂ����鉷�x�ω��ɒ��ڂ���ƁA
�@���@�ƂȂ�B����A���̉ߒ��ɂ����鉷�x�ω��ɒ��ڂ���ƁA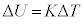 �Ƃ��\����B����䂦�A���̃q����f�M�I�ɂ������L�����ꍇ�A���x�̕ω�
�Ƃ��\����B����䂦�A���̃q����f�M�I�ɂ������L�����ꍇ�A���x�̕ω�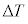 �́AA�CK�C
�́AA�CK�C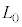 �CL�CT,
�CL�CT,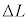 ��p����
��p����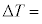 �@���@�ƕ\����B
�@���@�ƕ\����B
���̃q���̏�ԕω���g�ݍ��킹�āA�ȉ��̉ߒ�α�C�ߒ�β�C�ߒ�γ�C�ߒ�δ��4�̉ߒ�����Ȃ�M�͊w�I�ȃT�C�N�����l����B �E�@�ߒ�α�ł́A���x��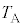 �ɕۂ����܂܁A����L��
�ɕۂ����܂܁A����L��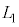 ����
����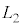 �ɂȂ�܂ŁA�������q���������B
�ɂȂ�܂ŁA�������q���������B �E�@�ߒ�β�ł́A����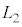 �̂܂܁A���x��
�̂܂܁A���x��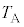 ����
����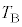 �ɏ㏸������B
�ɏ㏸������B �E�@�ߒ�γ�ł́A���x��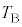 �ɕۂ����܂܁A����L��ς��A
�ɕۂ����܂܁A����L��ς��A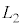 ����
����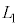 �܂ŁA�������߂��B
�܂ŁA�������߂��B �E�@�ߒ�δ�ł́A����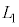 �̂܂܁A���x��
�̂܂܁A���x��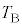 ����
����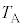 �ɖ߂��B
�ɖ߂��B �Ȃ��A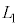 �C
�C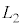 �C
�C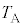 �C
�C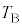 �́A���鐳�̒萔�ł���A
�́A���鐳�̒萔�ł���A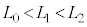 �C
�C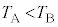 �����B
�����B
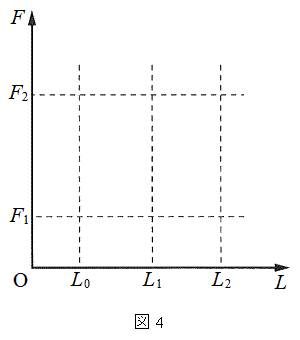 ��1�@�}4�����ɕ`���ʂ��C�ߒ�α�C�ߒ�β�C�ߒ�γ�C�ߒ�δ����Ȃ�T�C�N�����A�q���̒���L�������A�q���̒��͂̑傫��F���c���Ƃ��ăO���t�Ɏ����B���̍ہA�ߒ�α�̍ŏ��̏�Ԃ̒��͂̑傫����
��1�@�}4�����ɕ`���ʂ��C�ߒ�α�C�ߒ�β�C�ߒ�γ�C�ߒ�δ����Ȃ�T�C�N�����A�q���̒���L�������A�q���̒��͂̑傫��F���c���Ƃ��ăO���t�Ɏ����B���̍ہA�ߒ�α�̍ŏ��̏�Ԃ̒��͂̑傫����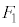 �C�ߒ�β�̍Ō�̏�Ԃ̒��͂̑傫����
�C�ߒ�β�̍Ō�̏�Ԃ̒��͂̑傫����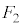 �Ƃ��āA�e�ߒ��ɂ�����L��F�̕ω��������Ŏ����A���ꂼ��̐���α�Cβ�Cγ�Cδ�̋L�������ĕ\���B�܂��A��}�ɕK�v�ȕ⏕����j���Ŏ����ƂƂ��ɁA��ԕω��̌��������������L������B
�Ƃ��āA�e�ߒ��ɂ�����L��F�̕ω��������Ŏ����A���ꂼ��̐���α�Cβ�Cγ�Cδ�̋L�������ĕ\���B�܂��A��}�ɕK�v�ȕ⏕����j���Ŏ����ƂƂ��ɁA��ԕω��̌��������������L������B
���̃T�C�N���̊e�ߒ��Ńq�����O���ɂ���d�����݂Ă݂悤�B�e�ߒ��Ńq��������d���́A������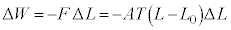 �̑��a�ł��邪�A���̑傫���́A��1�̃O���t�ɂ����āA�Ή�����ʐς����߂邱�Ƃł��v�Z�ł���B
�̑��a�ł��邪�A���̑傫���́A��1�̃O���t�ɂ����āA�Ή�����ʐς����߂邱�Ƃł��v�Z�ł���B
�ߒ�α�ɂ����ăq��������d��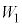 �́A
�́A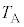 �C
�C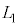 �C
�C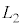 �CA�C
�CA�C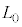 ��p����ƁA
��p����ƁA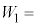 �@���@�ƕ\�����B�ߒ�γ�ɂ����ăq��������d��
�@���@�ƕ\�����B�ߒ�γ�ɂ����ăq��������d��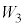 �́A
�́A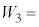 �@���@
�@���@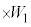 �ƕ\�����B�q�����ߒ�β�ł���d��
�ƕ\�����B�q�����ߒ�β�ł���d��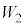 �Ɖߒ�δ�ł���d��
�Ɖߒ�δ�ł���d��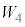 �́A
�́A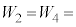 �@���@�ł���B�ȏ���A����1�T�C�N���ɂ����āA�q�����O���ɑ��Ă���d���̑��ʂ́A{���F�@���C�A0�C�B��}�ł��邱�Ƃ��킩��B
�@���@�ł���B�ȏ���A����1�T�C�N���ɂ����āA�q�����O���ɑ��Ă���d���̑��ʂ́A{���F�@���C�A0�C�B��}�ł��邱�Ƃ��킩��B
��2�@(1)�̗��z�C�̂�(2)�̃q���ł́A�n�̒���L��ω�������ۂ̔M�͊w�I�ȉ������قȂ�B�f�M�I�ɒ���L��傫������ꍇ���ɂƂ�A���z�C�̂���уq��������d���̈Ⴂ�ɒ��ڂ��A���҂̓����G�l���M�[����щ��x�̑��������ꂼ���������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���z�C�̂ƃq���Ƃ̔M�͊w�I�����̈Ⴂ���l���Ă݂悤�Ƃ������ł��B��蕶�ɏ����Ă��铹�����ɉ����đf���ɉł��܂��B
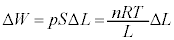 �@
�@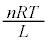 ......[��]
......[��]�ߒ��T�ł́A�����ω��œ����G�l���M�[�͕ω������̐ς�����̂ŋC�̂̂����d���͕��A�M�͊w���@�����A�C�͔̂r�M���Ă��܂��B
�ߒ��U�ł́A��ϕω��ŋC�͎̂d���������A���x���㏸����̂ŋC�̂̓����G�l���M�[�̕ω��͐��A�C�̂͋z�M���Ă��܂��B
�ߒ��V�ł́A�����ω��ő̐ς���������̂ŁA�C�̂͋z�M���Ă��܂��B
�ߒ��W�ł́A��ϕω��ʼn��x��������̂ŋC�͔̂r�M���Ă��܂��B
�C�̂��z�M���Ă���̂́A�A�ߒ��U�ƇB�ߒ��V�ł��B�@�A�C�B ......[��]�ߒ��U�Ɖߒ��W�ł͋C�̂̂����d����0�ŁA[��]�̌��ʂōl���āA�d���̐�Βl��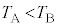 ���ߒ��T�����ߒ��V�̕����傫���A�ߒ��V�����ʼnߒ��W�����Ȃ̂ŋC�̂��O���ɑ��Ă���d���̑��ʂ͐��ł��B�@�@�� ......[��]
���ߒ��T�����ߒ��V�̕����傫���A�ߒ��V�����ʼnߒ��W�����Ȃ̂ŋC�̂��O���ɑ��Ă���d���̑��ʂ͐��ł��B�@�@�� ......[��]
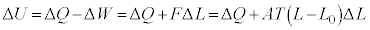 ......[��]
......[��]�q�����L�т�Ƃ��C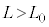 �C
�C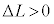 ��
��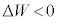 �C�܂�q�����O���ɕ��̎d�������邱�Ƃɒ��ӂ��Ă��������B
�C�܂�q�����O���ɕ��̎d�������邱�Ƃɒ��ӂ��Ă��������B
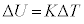 ���A�f�M�ω���
���A�f�M�ω���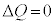 �̂Ƃ��ɂ́A[��]�̌��ʂ��A
�̂Ƃ��ɂ́A[��]�̌��ʂ��A 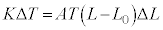 �@��
�@�� 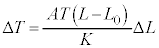 ......[��]
......[��]
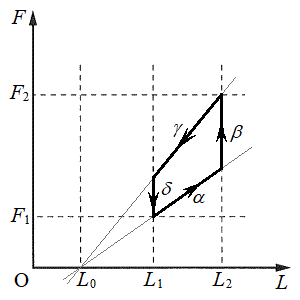 ��1�@�ߒ�α�ɂ����Ă�
��1�@�ߒ�α�ɂ����Ă�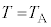 ���A
���A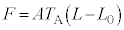 �C
�C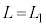 �̂Ƃ�
�̂Ƃ�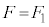 �Ȃ̂ŁA
�Ȃ̂ŁA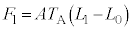 �C������A�ߒ�α�̃O���t�́A
�C������A�ߒ�α�̃O���t�́A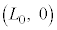 �C
�C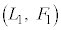 ��ʂ钼���ł��B�܂��A
��ʂ钼���ł��B�܂��A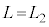 �̂Ƃ��A
�̂Ƃ��A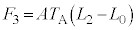 �ł��B
�ł��B�ߒ�β�ɂ����ẮA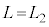 �̂܂܁AF��
�̂܂܁AF��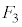 ����
����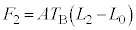 �܂ŕω����܂��B
�܂ŕω����܂��B
�ߒ�γ�ɂ����Ă�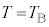 ���A
���A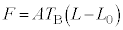 �C�ߒ�γ�̃O���t�́A
�C�ߒ�γ�̃O���t�́A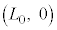 �C
�C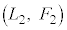 ��ʂ钼���ł��B
��ʂ钼���ł��B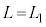 �̂Ƃ��A
�̂Ƃ��A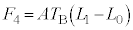 �ł��B
�ł��B
�ߒ�δ�ɂ����ẮA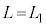 �̂܂܁AF��
�̂܂܁AF��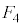 ����
����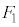 �܂ŕω����܂��B
�܂ŕω����܂��B
������}������ƉE�}(�⏕���́A�j���ł͂Ȃ��D�F�̒����ŕ`���Ă���܂�)�B
�ߒ�α�ŋC�̂̂����d�����E�}�ő�`�̖ʐς��狁�߂�ƁA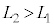 ���q���͐L�тĂ��āA�C�̂̂����d�������ł��邱�Ƃɒ��ӂ��āA
���q���͐L�тĂ��āA�C�̂̂����d�������ł��邱�Ƃɒ��ӂ��āA 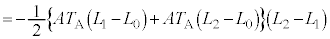
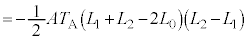 ......[��]
......[��]�ߒ�γ�ł́A�q���͒Z���Ȃ��Ă���̂ŋC�̂̂����d���͐��ŁA�ߒ�α�̉��x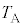 �����x
�����x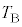 �ƂȂ�̂ŁA
�ƂȂ�̂ŁA 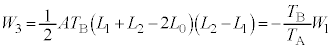 �@
�@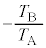 ......[��]
......[��]�ߒ�β�ł����d��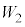 �C�ߒ�δ�ł̎d��
�C�ߒ�δ�ł̎d��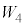 �́A
�́A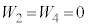 ......[��]���̉ߒ��Ńq�����O���ɑ��Ă���d���́A
......[��]���̉ߒ��Ńq�����O���ɑ��Ă���d���́A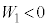 �C
�C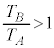 ���A
���A 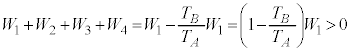 �@�@ ......[��]
�@�@ ......[��]
��2�@���z�C�̂Œf�M�I��L��傫������ƁA�܂�̐ς�������ƁA�C�̂̂����d��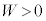 �Ȃ̂ŁA�M�͊w���@�����A
�Ȃ̂ŁA�M�͊w���@�����A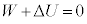 �C
�C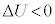 �C�����G�l���M�[�̕ω�
�C�����G�l���M�[�̕ω�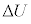 �͕��ŁA���x�͉�����܂��B
�͕��ŁA���x�͉�����܂��B �q���ł́A�f�M�I��L��傫������ƁA�q���������d��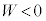 �Ȃ̂ŁA�M�͊w���@�����A�����G�l���M�[�̕ω�
�Ȃ̂ŁA�M�͊w���@�����A�����G�l���M�[�̕ω�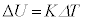 �͐��ŁA���x���㏸���܂��B ......[��]
�͐��ŁA���x���㏸���܂��B ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 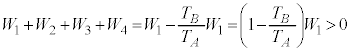 �@�@ ......[��]
�@�@ ......[��]