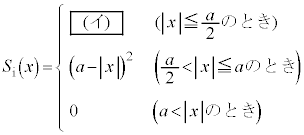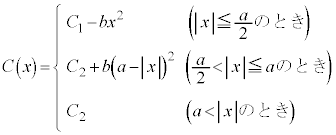東京工業大学2021年前期物理入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1] 水平な床の面に座標軸x,yをとり、その上で大きさが無視できる質量mの3つの小球A,B,Cを、長さLの2本の糸でB−A−Cの順につないだものをすべらせる実験を行う。糸は伸び縮みせず、その質量は無視でき、床と小球の間に摩擦はないものとする。また、床は十分広く、運動の途中で小球が床の端に達することはない。
 [A] 小球Aを原点に、小球Bと小球Cをy軸上の
[A] 小球Aを原点に、小球Bと小球Cをy軸上の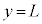 と
と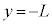 の位置に、それぞれ静止させる。時刻
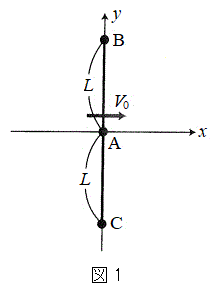
の位置に、それぞれ静止させる。時刻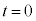 において、図1のように、小球Aにのみx軸の正の向きに速さ
において、図1のように、小球Aにのみx軸の正の向きに速さ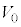 を与えて運動を開始させた。その後の小球の運動を観察したところ、運動開始直後は小球Bと小球Cの速度は0であり、その後小球Bと小球Cは近づいていき、やがてx軸上のある点で衝突した。運動の開始から衝突までの間、糸はたるむことはなく、小球Aから見ると、小球Bと小球Cは小球Aを中心とする円運動をした。以下の問に答えよ。
を与えて運動を開始させた。その後の小球の運動を観察したところ、運動開始直後は小球Bと小球Cの速度は0であり、その後小球Bと小球Cは近づいていき、やがてx軸上のある点で衝突した。運動の開始から衝突までの間、糸はたるむことはなく、小球Aから見ると、小球Bと小球Cは小球Aを中心とする円運動をした。以下の問に答えよ。
(a) 小球Bと小球Cが衝突する直前における、小球Bの速度のx成分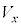 を
を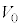 を用いて表せ。
を用いて表せ。
(b) 小球Bと小球Cが衝突する直前における、小球Bの速度のy成分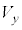 を
を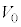 を用いて表せ。
を用いて表せ。
(c) 運動開始直後における、小球Bにつながれた糸の張力の大きさTを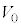 ,m,Lを用いて表せ。
,m,Lを用いて表せ。
(d) 小球Bと小球Cが衝突する直前における、小球Bにつながれた糸の張力の大きさ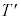 を
を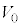 ,m,Lを用いて表せ。
,m,Lを用いて表せ。
 [B] 図2に示すように、小球Aを原点に、小球Bと小球Cをそれぞれ座標
[B] 図2に示すように、小球Aを原点に、小球Bと小球Cをそれぞれ座標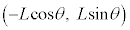 と
と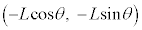 (
(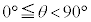 )の点に配置し、静止させる。時刻
)の点に配置し、静止させる。時刻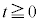 において、小球Aにx軸の正の向きに一定の大きさFの力を加える。以下のように、θの値を変えて実験1と実験2を行い、小球A,B,Cの運動を記録した。いずれの場合にも糸がたるむことはなかった。
において、小球Aにx軸の正の向きに一定の大きさFの力を加える。以下のように、θの値を変えて実験1と実験2を行い、小球A,B,Cの運動を記録した。いずれの場合にも糸がたるむことはなかった。
実験1: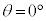 となるように、すなわち小球Bと小球Cが接するように、小球を配置し静止させる。そして
となるように、すなわち小球Bと小球Cが接するように、小球を配置し静止させる。そして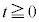 において小球Aにx軸の正の向きに一定の大きさFの力を加えたところ、小球Bと小球Cは接したまま、3つの小球はx軸の正の向きに同じ加速度で等加速度運動した。その加速度の大きさは
において小球Aにx軸の正の向きに一定の大きさFの力を加えたところ、小球Bと小球Cは接したまま、3つの小球はx軸の正の向きに同じ加速度で等加速度運動した。その加速度の大きさは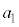 であった。
であった。
実験2:θをある値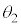 (
(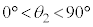 )にとり、
)にとり、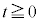 において小球Aにx軸の正の向きに一定の大きさFの力を加えたところ、小球Bと小球Cは時刻
において小球Aにx軸の正の向きに一定の大きさFの力を加えたところ、小球Bと小球Cは時刻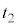 においてはじめて衝突した。衝突直前の小球Bと小球Cの速度ベクトルのなす角は
においてはじめて衝突した。衝突直前の小球Bと小球Cの速度ベクトルのなす角は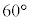 であった。
であった。 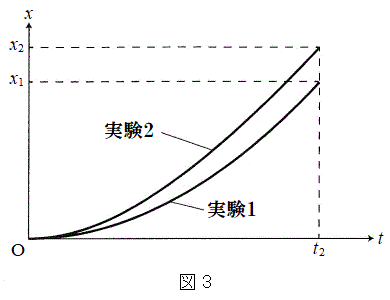 図3は実験1と実験2における小球Aのx座標の時間変化を
図3は実験1と実験2における小球Aのx座標の時間変化を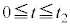 においてグラフにしたものである。ただし、グラフは概形である。
においてグラフにしたものである。ただし、グラフは概形である。
これらの実験における小球の運動に関する、以下の問に答えよ。
(e) 実験1における小球Aの加速度の大きさ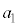 をmとFを用いて表せ。
をmとFを用いて表せ。
(f) 時刻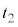 における実験1の小球Aの速さをvとする。実験2の小球Bの衝突直前における速さwをvを用いて表せ。
における実験1の小球Aの速さをvとする。実験2の小球Bの衝突直前における速さwをvを用いて表せ。
(g) 時刻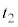 における実験1と実験2の小球Aのx座標をそれぞれ
における実験1と実験2の小球Aのx座標をそれぞれ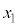 および
および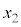 とする。比
とする。比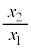 を求めよ。
を求めよ。 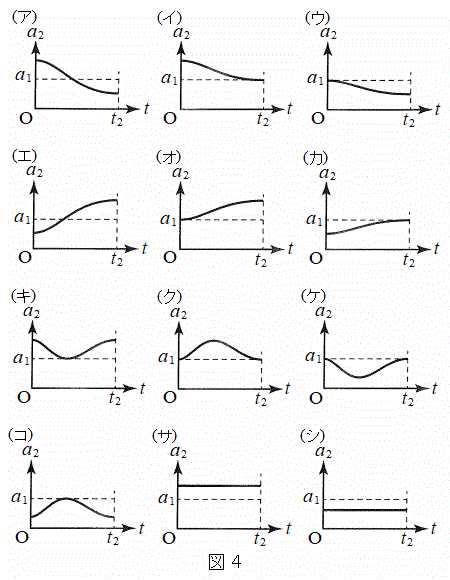 (h) 実験2の
(h) 実験2の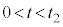 における小球Aの加速度の大きさ
における小球Aの加速度の大きさ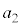 のグラフの概形として最も適当なものを図4の(ア)〜(シ)のうちから選び、記号で答えよ。
のグラフの概形として最も適当なものを図4の(ア)〜(シ)のうちから選び、記号で答えよ。
[解答へ]
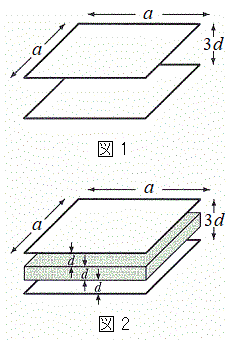 [2][A] 図1のように、真空中に2枚の薄い正方形の極板が水平に保たれて向かい合う平行板コンデンサーがある。極板の1辺の長さをa,2枚の極板のの間隔を
[2][A] 図1のように、真空中に2枚の薄い正方形の極板が水平に保たれて向かい合う平行板コンデンサーがある。極板の1辺の長さをa,2枚の極板のの間隔を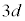 とする。また、図2はこの極板間に帯電していない誘電体の板を極板と平行に挿入したものである。誘電体は底面が1辺の長さaの正方形、高さがdの直方体であり、誘電体と上下の極板との間隔をdとする。誘電体の比誘電率を
とする。また、図2はこの極板間に帯電していない誘電体の板を極板と平行に挿入したものである。誘電体は底面が1辺の長さaの正方形、高さがdの直方体であり、誘電体と上下の極板との間隔をdとする。誘電体の比誘電率を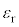 (
(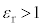 ),真空の誘電率を
),真空の誘電率を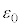 とする。極板の間隔
とする。極板の間隔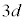 はaに比べて十分小さく、極板端部や誘電体端部における電場の乱れは無視できるものとする。以下の問に答えよ。
はaに比べて十分小さく、極板端部や誘電体端部における電場の乱れは無視できるものとする。以下の問に答えよ。
(a) 図1,図2のコンデンサーの電気容量をそれぞれ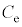 ,
,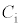 とする。
とする。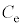 および
および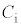 を、a,d,
を、a,d,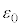 ,
,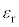 のうち必要なものを用いて表せ。
のうち必要なものを用いて表せ。
(b) 図1および図2のコンデンサーの極板間に0でない電位差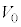 を与えると、図1の極板間、図2の上側極板と誘電体の間、および誘電体中には、それぞれ一様とみなすことのできる電場が生じる。それらの電場の強さをそれぞれ
を与えると、図1の極板間、図2の上側極板と誘電体の間、および誘電体中には、それぞれ一様とみなすことのできる電場が生じる。それらの電場の強さをそれぞれ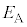 ,
,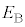 ,および
,および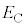 とする。
とする。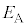 ,
,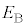 ,
,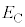 の大小関係を不等式
の大小関係を不等式 の形で答えよ。
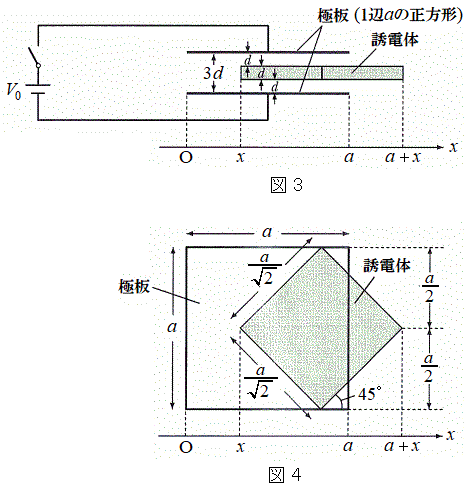 [B] 図3のように、図1の水平に置かれた平行板コンデンサーの極板間に誘電体の板を挿入した。このコンデンサーの両極板にスイッチおよび起電力
[B] 図3のように、図1の水平に置かれた平行板コンデンサーの極板間に誘電体の板を挿入した。このコンデンサーの両極板にスイッチおよび起電力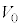 の直流電源をつないだ。x軸をこれらの極板のある1辺と平行にとり、両極板が
の直流電源をつないだ。x軸をこれらの極板のある1辺と平行にとり、両極板が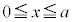 に存在するように原点を定める。誘電体は底面が1辺の長さ
に存在するように原点を定める。誘電体は底面が1辺の長さ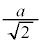 の正方形、高さがdの直方体であり、帯電していない。誘電体の比誘電率を
の正方形、高さがdの直方体であり、帯電していない。誘電体の比誘電率を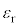 (
(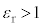 ),質量をmとする。鉛直上方から極板と誘電体の位置関係を見ると、図4のように、極板の各辺に対し、誘電体の4辺は
),質量をmとする。鉛直上方から極板と誘電体の位置関係を見ると、図4のように、極板の各辺に対し、誘電体の4辺は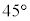 の角度をなしている。両極板が固定されているのに対し、誘電体は各極板を含む平面との間隔をdに保ちながら向きを変えることなくx方向にのみなめらかに動くことができる。誘電体の位置をその左端のx座標で表す。以下の問に答えよ。
の角度をなしている。両極板が固定されているのに対し、誘電体は各極板を含む平面との間隔をdに保ちながら向きを変えることなくx方向にのみなめらかに動くことができる。誘電体の位置をその左端のx座標で表す。以下の問に答えよ。なお、極板、スイッチ、導線の抵抗および電源の内部抵抗、回路の自己インダクタンス、電荷の移動に伴い放射される電磁波の影響、誘電体の分極の変化に伴う発熱は無視できるものとする。また、誘電体の移動に伴う極板上の電荷の再配置や誘電体の分極は十分速やかに起こるものとする。極板の間隔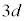 はaに比べて十分小さく、極板端部や誘電体端部における電場の乱れは無視できるものとする。
はaに比べて十分小さく、極板端部や誘電体端部における電場の乱れは無視できるものとする。
(c) 次の文章の空欄(ア)〜(オ)に当てはまる数式を答えよ。
誘電体の位置xが変化すると、極板の面積S (ただし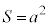 )のうち誘電体が挿入された部分の面積が変化する。これをxの関数として
)のうち誘電体が挿入された部分の面積が変化する。これをxの関数として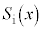 と表す。その結果、コンデンサーの電気容量もxの関数として変化する。これを
と表す。その結果、コンデンサーの電気容量もxの関数として変化する。これを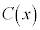 と表せば、問(b)で定義された
と表せば、問(b)で定義された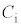 と
と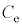 およびS,
およびS,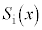 を用いて次のように表される。
を用いて次のように表される。 図4を参考に面積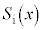 を求めれば、
を求めれば、 となる。したがって、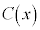 は次式の形で与えられる。
は次式の形で与えられる。 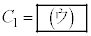 ,
,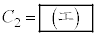
と表される。また、bはd,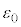 ,
,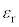 を用いて次式で表される。
を用いて次式で表される。
(d) 最初、誘電体は位置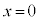 にあり、スイッチは閉じられているとする。その後、スイッチを開いてから誘電体の位置xを動かすと、コンデンサーに蓄えられる静電エネルギーはxの関数として変化する。これを
にあり、スイッチは閉じられているとする。その後、スイッチを開いてから誘電体の位置xを動かすと、コンデンサーに蓄えられる静電エネルギーはxの関数として変化する。これを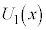 と表すとき、
と表すとき、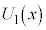 を
を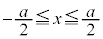 の範囲で、x,
の範囲で、x,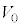 および問(c)で定義された
および問(c)で定義された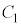 ,bを用いて表せ。
,bを用いて表せ。
(e) スイッチを閉じた状態で誘電体の位置xを動かすと、コンデンサーに蓄えられる静電エネルギーはxの関数として変化する。これを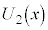 と表すとき、
と表すとき、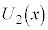 を
を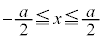 の範囲で、x,
の範囲で、x,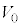 および問(c)で定義された
および問(c)で定義された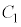 ,bを用いて表せ。
,bを用いて表せ。
(f) スイッチを閉じた状態で考える。誘電体の位置xを動かすと上側極板の電荷もxに応じて変化する。誘電体に外力を加えて位置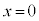 から位置xまでゆっくり動かす際に外力がする仕事
から位置xまでゆっくり動かす際に外力がする仕事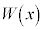 と電源が行う仕事との和が、コンデンサーの静電エネルギーの変化分に等しいことを用いて、
と電源が行う仕事との和が、コンデンサーの静電エネルギーの変化分に等しいことを用いて、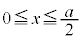 における
における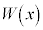 を求めよ。答はx,
を求めよ。答はx,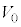 および問(c)で定義されたbを用いて表せ。ただし、起電力
および問(c)で定義されたbを用いて表せ。ただし、起電力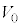 の電源が行う仕事は、電源の内部を負極から正極へ電荷Qが移動するとき、
の電源が行う仕事は、電源の内部を負極から正極へ電荷Qが移動するとき、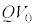 で与えられる。
で与えられる。
(g) スイッチを閉じた状態で、誘電体を位置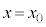 (
(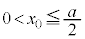 )から初速度0で放したところ、誘電体にはx方向の復元力が作用し、誘電体は振動した。問(f)の
)から初速度0で放したところ、誘電体にはx方向の復元力が作用し、誘電体は振動した。問(f)の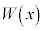 が誘電体の位置エネルギーとみなすことができることを用いて、位置xにおける復元力Fおよび振動の周期Tを求めよ。ただし、x軸の正方向を力Fの正の向きとする。答は、Fについてはx,
が誘電体の位置エネルギーとみなすことができることを用いて、位置xにおける復元力Fおよび振動の周期Tを求めよ。ただし、x軸の正方向を力Fの正の向きとする。答は、Fについてはx,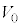 および問(c)で定義されたbを用いて表し、Tについてはa,d,
および問(c)で定義されたbを用いて表し、Tについてはa,d,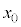 ,m,
,m,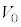 ,
,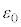 ,
,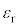 のうち必要なものを用いて表せ。
のうち必要なものを用いて表せ。
(h) スイッチを閉じた状態で、誘電体を位置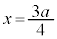 から初速度0で放したところ、誘電体は位置xが小さくなる向きに動き出した。位置
から初速度0で放したところ、誘電体は位置xが小さくなる向きに動き出した。位置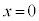 となったときの誘電体の速さを
となったときの誘電体の速さを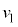 とする。
とする。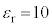 として、
として、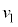 をa,d,m,
をa,d,m,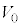 ,
,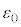 のうち必要なものを用いて表せ。
のうち必要なものを用いて表せ。 [解答へ]
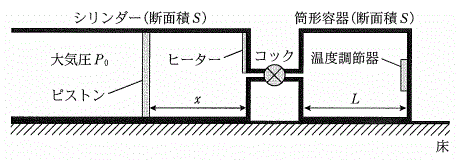 [3] 図のように、シリンダー、ピストン、筒型容器からなる装置を考える。十分に長いシリンダー(断面積S)と長さLの筒型容器(断面積S)は、水平な床の上に固定されており、コックのついた管でつながっている。シリンダーには水平方向になめらかに動くピストンがあり、シリンダー内の気体と大気を仕切ることができる。シリンダー底面からピストンの内面までの距離xを用いて、ピストンの位置を表す。また、シリンダーの中にはヒーターがあり、シリンダー内の気体を加熱することができる。筒型容器には温度調節器があり、気体との間で熱を自由にやりとりすることにより容器内の気体の温度を制御することができる。シリンダー、ピストン、筒型容器、コックのついた管は熱を通さない物質でできており、コックのついた管、ヒーターならびに温度調節器の体積と熱容量は無視できる。大気の圧力(大気圧)は
[3] 図のように、シリンダー、ピストン、筒型容器からなる装置を考える。十分に長いシリンダー(断面積S)と長さLの筒型容器(断面積S)は、水平な床の上に固定されており、コックのついた管でつながっている。シリンダーには水平方向になめらかに動くピストンがあり、シリンダー内の気体と大気を仕切ることができる。シリンダー底面からピストンの内面までの距離xを用いて、ピストンの位置を表す。また、シリンダーの中にはヒーターがあり、シリンダー内の気体を加熱することができる。筒型容器には温度調節器があり、気体との間で熱を自由にやりとりすることにより容器内の気体の温度を制御することができる。シリンダー、ピストン、筒型容器、コックのついた管は熱を通さない物質でできており、コックのついた管、ヒーターならびに温度調節器の体積と熱容量は無視できる。大気の圧力(大気圧)は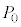 で一定である。以下の問に答えよ。ただし、気体定数をRとする。
で一定である。以下の問に答えよ。ただし、気体定数をRとする。
最初、ピストンの位置は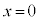 で、コックが閉じられており、筒型容器には単原子分子理想気体が閉じ込められていた。コックを開いたところ、筒型容器内の気体が管を通ってシリンダー内に膨張した。しばらくすると、装置内の気体の状態が一様となり、ピストンは位置
で、コックが閉じられており、筒型容器には単原子分子理想気体が閉じ込められていた。コックを開いたところ、筒型容器内の気体が管を通ってシリンダー内に膨張した。しばらくすると、装置内の気体の状態が一様となり、ピストンは位置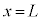 で静止した。このときの装置内の気体の温度を
で静止した。このときの装置内の気体の温度を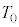 とする。ここで、コックを閉じた。コックを閉じた後の装置内の気体の状態を、状態Aとよぶ。
とする。ここで、コックを閉じた。コックを閉じた後の装置内の気体の状態を、状態Aとよぶ。
次に、ピストンの位置を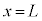 に固定するようピストンに外力を加えたまま、シリンダー内の気体をヒーターでゆっくり加熱したところ、その気体の圧力は
に固定するようピストンに外力を加えたまま、シリンダー内の気体をヒーターでゆっくり加熱したところ、その気体の圧力は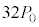 となり、ここで加熱をやめた。このときの装置内の気体の状態を、状態Bとよぶ。
となり、ここで加熱をやめた。このときの装置内の気体の状態を、状態Bとよぶ。
(a) 状態Bにおけるシリンダー内の気体の温度を求めよ。答のみ記せ。
(b) 状態Aから状態Bへの過程において、ヒーターがシリンダー内の気体に加えた熱量を求めよ。答のみ記せ。
続いて、ピストンに加える外力を徐々に弱めながら、シリンダー内の気体の圧力が大気圧と等しくなるまで、シリンダー内の気体を断熱的に膨張させた。この状態を、状態Cとよぶ。状態Bから状態Cへの過程において、シリンダー内の気体は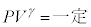 の関係式を満たす。ここでP,Vはそれぞれ、シリンダー内の気体の圧力、体積であり、
の関係式を満たす。ここでP,Vはそれぞれ、シリンダー内の気体の圧力、体積であり、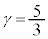 である。
である。
(c) 状態Cにおけるピストンの位置xの値を求めよ。
(d) 状態Bから状態Cへの過程において、シリンダー内の気体が外部にした仕事を求めよ。
次に、ピストンが動かないように固定し、さらにコックを開いてしばらくすると、装置内の気体の状態が一様になった。この状態を、状態Dとよぶ。状態Cから状態Dへの過程において、装置内の気体と外部の間で熱のやりとりはなく、また気体は外部に仕事をしないため、装置内の気体の内部エネルギーは変化しない。
(e) 状態Dにおける装置内の気体の温度、圧力を求めよ。
(f) 状態Cから状態Dへの過程において、筒型容器からシリンダーへ移動した気体のモル数を求めよ。
その後、ピストンの固定をはずし、さらにコックを開いたまま温度調節器を用いて装置内の気体から熱をゆっくり吸収し、装置内の気体の温度を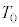 にしたところ、ピストンの位置が
にしたところ、ピストンの位置が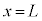 に戻った。ここで、コックを閉じた。このことにより、装置内の気体の状態は元の状態Aに戻った。
に戻った。ここで、コックを閉じた。このことにより、装置内の気体の状態は元の状態Aに戻った。
(g) 状態Dから元の状態Aに戻る過程において、温度調節器が装置内の気体から吸収した熱量を求めよ。
(h) この装置内の気体の状態が、状態Aから状態B,C,Dを経て状態Aに戻る過程を熱機関のサイクルと考えることができる。この熱機関の効率(熱効率)を求めよ。 [解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東工大物理TOP 物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。