�����H�Ƒ�w2022�N�O�������������
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
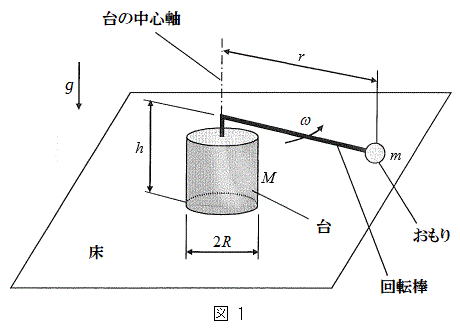 [1]�@�}1�̂悤�ɁA���a
[1]�@�}1�̂悤�ɁA���a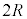 �̉~���`�̑�ƁA���̑�Ɏx������A��̒�ʂ���h�̍����̕��ʓ����̒��S������ɉ�]���钷��r (
�̉~���`�̑�ƁA���̑�Ɏx������A��̒�ʂ���h�̍����̕��ʓ����̒��S������ɉ�]���钷��r (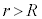 )�̉�]�_�ƁA���̉�]�_�̐�[�ɌŒ肳�ꂽ�傫���������ł��鎿��m�̂����肩��Ȃ鑕�u���A�����ȏ��̏�ɒu����Ă���B���̑�̓����ɂ̓��[�^�[������A�ォ�猩�Ĕ����v���ɉ�]�_����]�����邱�Ƃ��ł���B��]�_�̊p���xω�͎��R�ɕς��邱�Ƃ��ł���B���[�^�[���܂߂���̎��ʂ�M�ł���A���̏d�S�͑�̒��S����ɂ���B��]�_�͕ό`�����A���̎��ʂ͖����ł�����̂Ƃ���B�܂��A��C��R�͖����ł�����̂Ƃ���B�d�͉����x��
)�̉�]�_�ƁA���̉�]�_�̐�[�ɌŒ肳�ꂽ�傫���������ł��鎿��m�̂����肩��Ȃ鑕�u���A�����ȏ��̏�ɒu����Ă���B���̑�̓����ɂ̓��[�^�[������A�ォ�猩�Ĕ����v���ɉ�]�_����]�����邱�Ƃ��ł���B��]�_�̊p���xω�͎��R�ɕς��邱�Ƃ��ł���B���[�^�[���܂߂���̎��ʂ�M�ł���A���̏d�S�͑�̒��S����ɂ���B��]�_�͕ό`�����A���̎��ʂ͖����ł�����̂Ƃ���B�܂��A��C��R�͖����ł�����̂Ƃ���B�d�͉����x��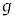 �Ƃ���B
�Ƃ���B
[A]�@��Ə��̊Ԃ̐Î~���C�W����μ�Ƃ���BR�Cr�Ch�CM�Cm�Cμ���قȂ镡���̑��u�����A���̏�ɒu���āA��]�_����ё䂪�Î~������Ԃ����]�_�̊p���x���������Ƒ傫�����Ă������B����ƁA���u�̈Ⴂ�ɂ���ĉ��L��2�̏ꍇ�����邱�Ƃ��킩�����B
�y�T�z�@�䂪�X�����ƂȂ���]�_�̕����ɏ��̏������n�߂�
�y�U�z�@�䂪���̏�����邱�ƂȂ���]�_�̕����ɌX���n�߂�
�������A�y�T�z�C�y�U�z���N����O�ɁA�䂪���ɑ��ĉ�]���邱�Ƃ͂Ȃ������B�ȉ��̖�ɓ�����B
(a) ��]�_����]���Ă��Ȃ��Ƃ��A�䂪�|��Ȃ����߂ɂ́A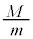 ������l�ȏ�łȂ���Ȃ�Ȃ��B���̏��������L�̎��ŕ\���Ƃ��A��(�A)�ɓ���K�Ȑ�����R��r��p���ĕ\���B
������l�ȏ�łȂ���Ȃ�Ȃ��B���̏��������L�̎��ŕ\���Ƃ��A��(�A)�ɓ���K�Ȑ�����R��r��p���ĕ\���B
(b) �y�T�z���N����ꍇ�A�䂪���̏������n�߂�Ƃ��̉�]�_�̊p���x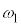 ��r�CM�Cm�Cμ�C
��r�CM�Cm�Cμ�C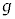 ��p���ĕ\���B
��p���ĕ\���B
(c) �y�U�z���N����ꍇ�A�䂪�X���n�߂�Ƃ��̉�]�_�̊p���x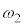 ��R�Cr�Ch�CM�Cm�C
��R�Cr�Ch�CM�Cm�C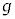 ��p���ĕ\���B
��p���ĕ\���B
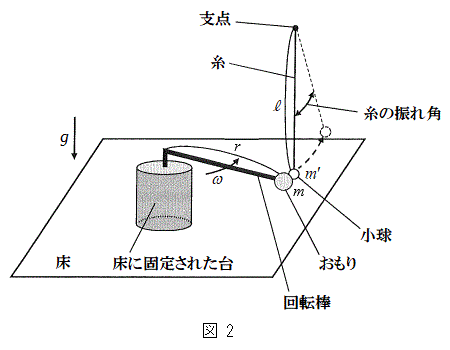 [B]�@������̏�ɌŒ肵�A���[�^�[�ɂ���]�_�����̊p���xω�ʼn�]�����Ă����B���[�^�[�͏[�����͂ŁA������͏�ɓ����~�^���𑱂�����̂Ƃ���B���̏�Ԃɂ����āA�}2�̂悤�ɁA����
[B]�@������̏�ɌŒ肵�A���[�^�[�ɂ���]�_�����̊p���xω�ʼn�]�����Ă����B���[�^�[�͏[�����͂ŁA������͏�ɓ����~�^���𑱂�����̂Ƃ���B���̏�Ԃɂ����āA�}2�̂悤�ɁA����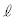 �̎��Ƒ傫���������ł��鎿��
�̎��Ƒ傫���������ł��鎿�� �̏�������Ȃ�U��q���������~�낵�Ă����A�����肪�ʂ�~�O����ɏ�����Î~�������B���̌�A�U��q�̎x�_(�����Ƃ͋t���̎��̒[)�̈ʒu�͕ς��Ȃ����̂Ƃ���B
�̏�������Ȃ�U��q���������~�낵�Ă����A�����肪�ʂ�~�O����ɏ�����Î~�������B���̌�A�U��q�̎x�_(�����Ƃ͋t���̎��̒[)�̈ʒu�͕ς��Ȃ����̂Ƃ���B����ƁA������Ə������Փ˂��A�����͏Փˎ��̂�����̐i�s�����ɑ���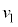 �œ����o�����B���̌�A�����͒P�U��q�̉^�����s���A�B�ĂяՓ˒n�_�܂ō~��Ă����B���̊ԁA��]�_�͑�̎����������āA������Ə�����1��ڂ̏Փ˂Ɠ����ʒu��2��ڂ̏Փ˂��s���A�����͏Փˎ��̂�����̐i�s�����ɑ���
�œ����o�����B���̌�A�����͒P�U��q�̉^�����s���A�B�ĂяՓ˒n�_�܂ō~��Ă����B���̊ԁA��]�_�͑�̎����������āA������Ə�����1��ڂ̏Փ˂Ɠ����ʒu��2��ڂ̏Փ˂��s���A�����͏Փˎ��̂�����̐i�s�����ɑ���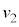 �œ����o�����B�����Ƃ�����̊Ԃ̔����W����e�Ƃ���B
�œ����o�����B�����Ƃ�����̊Ԃ̔����W����e�Ƃ���B
����2��Փ˂̎�����r�C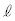 �Ce�Cm�C
�Ce�Cm�C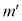 ���قȂ镡���̑��u�ƐU��q��p���čs�����B�������A��L�̏Փ˂��N����悤�ɁA���ꂼ��̑��u�ƐU��q�ɂ����ĉ�]�_�̊p���xω��K�ɐݒ肵���B���͐L�т��A���̎��ʂ͖����ł�����̂Ƃ���B�܂��A���̐U��p(�����������ƂȂ��p)��
���قȂ镡���̑��u�ƐU��q��p���čs�����B�������A��L�̏Փ˂��N����悤�ɁA���ꂼ��̑��u�ƐU��q�ɂ����ĉ�]�_�̊p���xω��K�ɐݒ肵���B���͐L�т��A���̎��ʂ͖����ł�����̂Ƃ���B�܂��A���̐U��p(�����������ƂȂ��p)��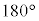 ���邱�Ƃ͂Ȃ����̂Ƃ���B�ȉ��̖�ɓ�����B
���邱�Ƃ͂Ȃ����̂Ƃ���B�ȉ��̖�ɓ�����B
(d) 1��ڂ̏Փ˒���̏����̑���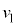 ��2��ڂ̏Փ˒���̏����̑���
��2��ڂ̏Փ˒���̏����̑���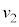 ��r�Ce�Cω��p���Ă��ꂼ��\���B
��r�Ce�Cω��p���Ă��ꂼ��\���B
(e) ���鑕�u�ƐU��q��p���Ď������s�����Ƃ���A���̐U��p�͏[���ɏ����������B���̂Ƃ��A�����̉^����P�U���Ƃ݂Ȃ����Ƃɂ��A��]�_�̊p���xω��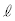 ��
��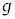 ��p���ĕ\���B
��p���ĕ\���B 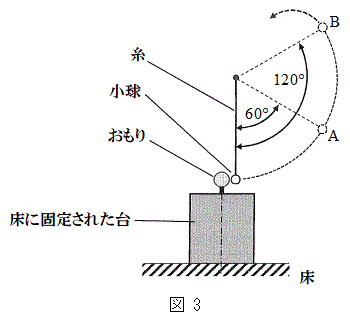 (f) �O��(e)�Ƃ͈قȂ鑕�u�ƐU��q��p���Ď������s�����Ƃ���A���̐U��p�͑傫���Ȃ����B�}3�́A���̎����ɂ����鏬���̉^���̗l�q���A�������������ʂɑ������ȕ������猩���}�ł���B1��ڂ̏Փˌ�A�����͎��̐U��p��
(f) �O��(e)�Ƃ͈قȂ鑕�u�ƐU��q��p���Ď������s�����Ƃ���A���̐U��p�͑傫���Ȃ����B�}3�́A���̎����ɂ����鏬���̉^���̗l�q���A�������������ʂɑ������ȕ������猩���}�ł���B1��ڂ̏Փˌ�A�����͎��̐U��p��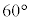 �ƂȂ�ʒuA�ōō��_�ɒB�����B���̂��Ƃ���A1��ڂ̏Փ˒���̏����̑���
�ƂȂ�ʒuA�ōō��_�ɒB�����B���̂��Ƃ���A1��ڂ̏Փ˒���̏����̑���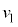 ��
��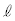 ��
��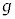 ��p���ĕ\���B
��p���ĕ\���B
(g) �O��(f)�̎����ɂ����āA2��ڂ̏Փˌ�A�����͎��̐U��p��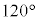 �ƂȂ�ʒuB�ɒB�����B�ʒuB�ɏ������B����܂Ŏ��͂���܂Ȃ��������A�������ʒuB�ɒB�������ォ�玅�͂���݁A�����͕����^�����n�߂��B���̂��Ƃ���A2��ڂ̏Փ˒���̏����̑���
�ƂȂ�ʒuB�ɒB�����B�ʒuB�ɏ������B����܂Ŏ��͂���܂Ȃ��������A�������ʒuB�ɒB�������ォ�玅�͂���݁A�����͕����^�����n�߂��B���̂��Ƃ���A2��ڂ̏Փ˒���̏����̑���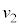 ��
��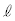 ��
��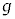 ��p���ĕ\���B
��p���ĕ\���B
(h) ��(d)�C(f)�C(g)�̌��ʂ𗘗p���āA��(f)�����(g)�̎����ɂ����鏬���Ƃ�����̊Ԃ̔����W��e�̒l�����߂�B
[��]
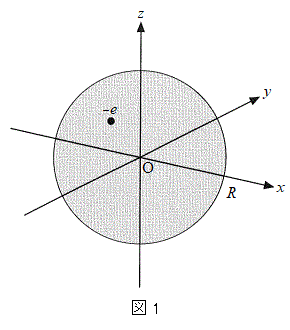 [2]�@N�𐳂̐����Ƃ���B�^�ɂ����āA����
[2]�@N�𐳂̐����Ƃ���B�^�ɂ����āA����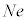 �̐��d�ׂ����aR�̋����Ɉ�l�ɕ��z���A���d��
�̐��d�ׂ����aR�̋����Ɉ�l�ɕ��z���A���d��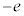 �����דd���q��N�������݂���Ƃ���B���̋��̒��S�����_O�Ƃ��āA�݂��ɒ�������悤��x���Cy���Cz����݂���B���̂Ƃ��A���d�ׂ̕��z�����_���狗��r�������ꂽ�_�ɂ���d��́A���_�𒆐S�Ƃ��锼�ar�̋������̐��d�ׂ��S�Č��_�ɏW�������ƍl�����Ƃ��ɐ�����d��ɓ������A���̊O���̐��d�ׂɂ͂��Ȃ����Ƃ��m���Ă���B�}1�́A
�����דd���q��N�������݂���Ƃ���B���̋��̒��S�����_O�Ƃ��āA�݂��ɒ�������悤��x���Cy���Cz����݂���B���̂Ƃ��A���d�ׂ̕��z�����_���狗��r�������ꂽ�_�ɂ���d��́A���_�𒆐S�Ƃ��锼�ar�̋������̐��d�ׂ��S�Č��_�ɏW�������ƍl�����Ƃ��ɐ�����d��ɓ������A���̊O���̐��d�ׂɂ͂��Ȃ����Ƃ��m���Ă���B�}1�́A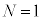 �̏ꍇ�ɁA���d�ׂ̕��z�Ɖדd���q�̈ʒu�̗�����������̂ł���B
�̏ꍇ�ɁA���d�ׂ̕��z�Ɖדd���q�̈ʒu�̗�����������̂ł���B
�דd���q�̎��ʂ�m�C�N�[�����̖@���̔��萔��k�Ƃ��A���d�ׂ̕��z�͕s�ςœ������A�דd���q�ɑ��ĐÓd�C�͈ȊO�̗͂��y�ڂ��Ȃ����̂Ƃ���B�܂��A�d���g�̕��˂�d�͖͂����ł�����̂Ƃ���B
[A]�@�ȉ��̖�ɓ�����B
(a) �ȉ��̕��͒��̋�(�A)�`(�J)�ɓ��Ă͂܂�K�Ȑ������Ae�CR�Cm�Ck�̂����K�v�Ȃ��̂�p���ĕ\���B
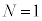 �̏ꍇ�ɁA�דd���q�����_���狗��r�������ꂽ�_�ɑ��݂���Ƃ��A���̉דd���q�����d�ׂ̕��z�����Ód�C�͂̑傫��F�ƁA���̐Ód�C�͂ɂ��דd���q�̈ʒu�G�l���M�[U���l����B�܂��A
�̏ꍇ�ɁA�דd���q�����_���狗��r�������ꂽ�_�ɑ��݂���Ƃ��A���̉דd���q�����d�ׂ̕��z�����Ód�C�͂̑傫��F�ƁA���̐Ód�C�͂ɂ��דd���q�̈ʒu�G�l���M�[U���l����B�܂��A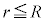 �̏ꍇ�ɂ�����Ód�C�͂͌��_�Ɍ������A���̑傫����
�̏ꍇ�ɂ�����Ód�C�͂͌��_�Ɍ������A���̑傫����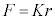 �̂悤��r�ɔ�Ⴕ�A���̔��萔��
�̂悤��r�ɔ�Ⴕ�A���̔��萔��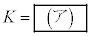 �ł���B�˂ɂ��e���͂Ɠ��l�ɗ͂̑傫����r�ɔ�Ⴗ��̂ŁA�דd���q�̈ʒu�G�l���M�[�́A���_����Ƃ���
�ł���B�˂ɂ��e���͂Ɠ��l�ɗ͂̑傫����r�ɔ�Ⴗ��̂ŁA�דd���q�̈ʒu�G�l���M�[�́A���_����Ƃ���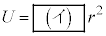 �ƂȂ�B
�ƂȂ�B
����A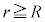 �̏ꍇ�ɂ�����Ód�C�͂����_�Ɍ������A���̑傫����
�̏ꍇ�ɂ�����Ód�C�͂����_�Ɍ������A���̑傫���� �̂悤��r�̓��ɔ���Ⴗ��B����āA�דd���q�̈ʒu�G�l���M�[�́A
�̂悤��r�̓��ɔ���Ⴗ��B����āA�דd���q�̈ʒu�G�l���M�[�́A �ƂȂ�B�����ŁAC��r�ɂ��Ȃ��萔�ł���A
�ƂȂ�B�����ŁAC��r�ɂ��Ȃ��萔�ł���A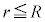 �ɂ�����ʒu�G�l���M�[��
�ɂ�����ʒu�G�l���M�[��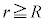 �ɂ�����ʒu�G�l���M�[�Ƃ�
�ɂ�����ʒu�G�l���M�[�Ƃ�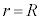 �ɂ����Ĉ�v���邱�Ƃ���A
�ɂ����Ĉ�v���邱�Ƃ���A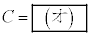 �ƒ�܂�B
�ƒ�܂�B
�ȏ�̌��ʂ�p����ƁA���_�ŐÎ~���Ă���דd���q�����ɂ܂ň����������߂ɕK�v�ƂȂ�ŏ��̎d��W�́A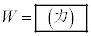 �ƂȂ邱�Ƃ��킩��B
�ƂȂ邱�Ƃ��킩��B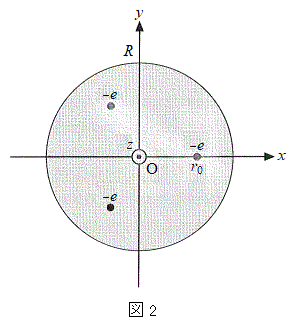 (b)
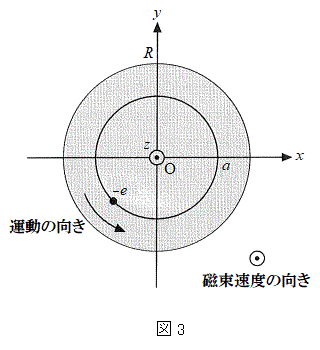
(b) 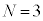 �̏ꍇ�ɁA���aR�̋����ɑ��݂���3�̉דd���q���l����B�}2�̂悤�ɁA����炪
�̏ꍇ�ɁA���aR�̋����ɑ��݂���3�̉דd���q���l����B�}2�̂悤�ɁA����炪 ��x-y���ʓ��ɂ����āA���_���d�S�Ƃ��鐳�O�p�`�̊e���_�ŐÎ~���A�����ł͐Ód�C�͂��荇���B���̂Ƃ��A���d�ׂ̑��ʂ�
��x-y���ʓ��ɂ����āA���_���d�S�Ƃ��鐳�O�p�`�̊e���_�ŐÎ~���A�����ł͐Ód�C�͂��荇���B���̂Ƃ��A���d�ׂ̑��ʂ�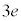 �ł��邱�Ƃɒ��ӂ��āA���_����דd���q�̈ʒu�܂ł̋���
�ł��邱�Ƃɒ��ӂ��āA���_����דd���q�̈ʒu�܂ł̋���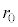 ���Ae�CR�Cm�Ck�̂����K�v�Ȃ��̂�p���ĕ\���B
���Ae�CR�Cm�Ck�̂����K�v�Ȃ��̂�p���ĕ\���B
 [B]�@
[B]�@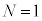 �̏ꍇ�ɁAz���̐��̌����Ɉ��ň�l�Ȏ���������A���̎������x�̑傫����B�Ƃ���B���̂Ƃ��A�}3�̂悤�ɁA
�̏ꍇ�ɁAz���̐��̌����Ɉ��ň�l�Ȏ���������A���̎������x�̑傫����B�Ƃ���B���̂Ƃ��A�}3�̂悤�ɁA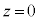 ��x-y���ʓ��ɂ����Č��_�𒆐S�Ƃ��锼�aa (
��x-y���ʓ��ɂ����Č��_�𒆐S�Ƃ��锼�aa (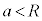 )�̉~�O������~�^������דd���q���l����B�דd���q�̊p���x��ω�Ƃ��A�����~�^���̌�����z���̐��̑����猩�Ĕ����v���ł���Ƃ���B�ȉ��̖�ɓ�����B
)�̉~�O������~�^������דd���q���l����B�דd���q�̊p���x��ω�Ƃ��A�����~�^���̌�����z���̐��̑����猩�Ĕ����v���ł���Ƃ���B�ȉ��̖�ɓ�����B
(c) �דd���q�̊p���xω�����߂�B�������A�{��ł́A[A]�̖�(a)��(�A)�ŋ��߂����萔��K�Ƃ����Ae�Cm�CB�CK�̂����K�v�Ȃ��̂�p���ĕ\���B
(d) �����~�^���̎��������[���ɒ������Ԃɂ킽���ĉ~�O����̂���_��ʉ߂���d�C�ʂς��邱�ƂŁA�~�O����𗬂��d��I�����߁Ae�Cm�Ca�Cω�̂����K�v�Ȃ��̂�p���ĕ\���B�������A�d���̌����������v���̂Ƃ�I�̒l�͐��A���v���̂Ƃ�I�̒l�͕��ƂȂ���̂Ƃ���B
(e) ��(d)�̓d�������_�ɂ��鎥���z����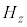 ���Ae�Cm�Ca�Cω�̂����K�v�Ȃ��̂�p���ĕ\���B
���Ae�Cm�Ca�Cω�̂����K�v�Ȃ��̂�p���ĕ\���B
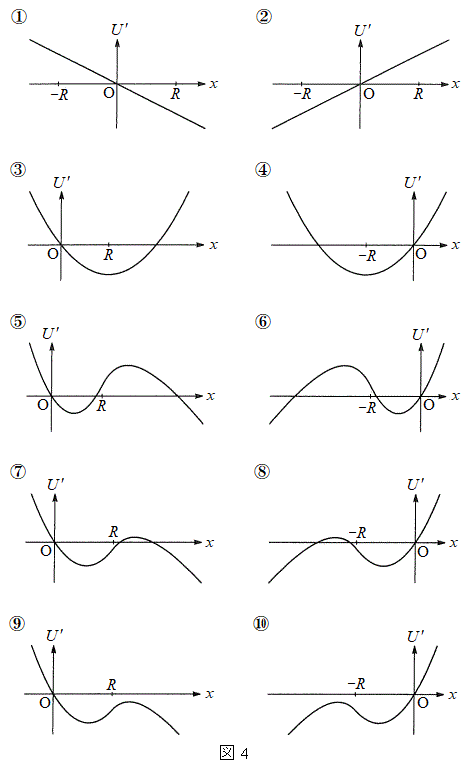 [C]�@
[C]�@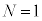 �̏ꍇ�ɁA���_�ŐÎ~���Ă���דd���q���l����B���鎞������x���̐��̌����Ɉ��ň�l�ȓd����������Ƃ���A�דd���q�͔��aR�̋����ɂƂǂ܂炸��x����ʼn����^�����n�߂����A�������ɂ܂œ��B���邱�Ƃ͂Ȃ������B�ȉ��̖�ɓ�����B
�̏ꍇ�ɁA���_�ŐÎ~���Ă���דd���q���l����B���鎞������x���̐��̌����Ɉ��ň�l�ȓd����������Ƃ���A�דd���q�͔��aR�̋����ɂƂǂ܂炸��x����ʼn����^�����n�߂����A�������ɂ܂œ��B���邱�Ƃ͂Ȃ������B�ȉ��̖�ɓ�����B
(f) �דd���q�̈ʒu�G�l���M�[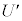 �́A���d�ׂ̕��z�����Ód�C�͂ɂ����̂ƈ�l�ȓd�ꂩ���Ód�C�͂ɂ����̘̂a�ŗ^������B���_����Ƃ���Ƃ��Ax����ɂ�����
�́A���d�ׂ̕��z�����Ód�C�͂ɂ����̂ƈ�l�ȓd�ꂩ���Ód�C�͂ɂ����̘̂a�ŗ^������B���_����Ƃ���Ƃ��Ax����ɂ�����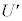 �̊T�`�Ƃ��čł��K���Ȃ��̂�}4�̑I�����@�`�I����I�сA�ԍ��œ�����B�������A���ꂼ��̃O���t�ɕ`����Ă���x�͈̔͊O�ł́A
�̊T�`�Ƃ��čł��K���Ȃ��̂�}4�̑I�����@�`�I����I�сA�ԍ��œ�����B�������A���ꂼ��̃O���t�ɕ`����Ă���x�͈̔͊O�ł́A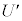 �͒P���ɑ������邢�͌�������������̂Ƃ���B
�͒P���ɑ������邢�͌�������������̂Ƃ���B
(g) �דd���q�����aR�̋����ɂƂǂ܂炸�ɉ^������悤�ȓd��̋����̉����ƂȂ�l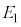 ���Ae�CR�Cm�Ck�̂����K�v�Ȃ��̂�p���ĕ\���B
���Ae�CR�Cm�Ck�̂����K�v�Ȃ��̂�p���ĕ\���B
(h) �דd���q���������ɂ܂œ��B���Ȃ��悤�ȓd��̋����̏���ƂȂ�l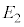 ���Ae�CR�Cm�Ck�̂����K�v�Ȃ��̂�p���ĕ\���B
���Ae�CR�Cm�Ck�̂����K�v�Ȃ��̂�p���ĕ\���B [��]
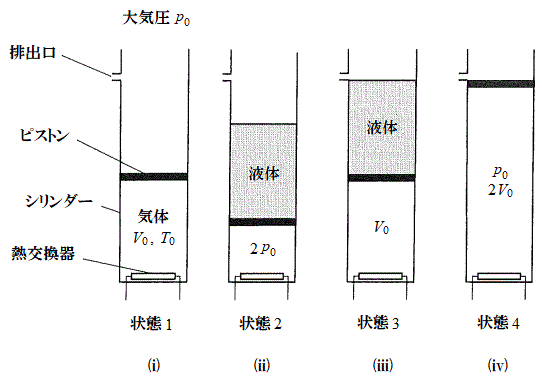 [3]�@�}�̂悤�ɉ��������Ɋ��炩�ɓ����s�X�g���������V�����_�[�ɁA1�����̒P���q���q���z�C�̂������߂��Ă���B�s�X�g���̏㕔�ɂ͉t�̂����߂���悤�ɂȂ��Ă���B�܂��A�V�����_�[�ɂ̓s�X�g���̏���̈ʒu�ɉt�̂̔r�o�����J�����Ă���B�V�����_�[�͑�C���ɒu����A��C���͏��
[3]�@�}�̂悤�ɉ��������Ɋ��炩�ɓ����s�X�g���������V�����_�[�ɁA1�����̒P���q���q���z�C�̂������߂��Ă���B�s�X�g���̏㕔�ɂ͉t�̂����߂���悤�ɂȂ��Ă���B�܂��A�V�����_�[�ɂ̓s�X�g���̏���̈ʒu�ɉt�̂̔r�o�����J�����Ă���B�V�����_�[�͑�C���ɒu����A��C���͏��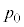 �ł���Ƃ���B�V�����_�[�����ɂ̓V�����_�[���̋C�̂����M�܂��͗�p�ł���M�����킪�ݒu����Ă���B�V�����_�[�ƃs�X�g���͒f�M�ނłł��Ă���A�s�X�g���̎��ʂ���݂͖����ł�����̂Ƃ���B����ɁA�V�����_�[�A�s�X�g���A�M������̔M�e�ʂƂ��߂�ꂽ�t�̂̏����͖����ł�����̂Ƃ���B�C�̒萔��R�Ƃ��āA�ȉ��̖�ɓ�����B
�ł���Ƃ���B�V�����_�[�����ɂ̓V�����_�[���̋C�̂����M�܂��͗�p�ł���M�����킪�ݒu����Ă���B�V�����_�[�ƃs�X�g���͒f�M�ނłł��Ă���A�s�X�g���̎��ʂ���݂͖����ł�����̂Ƃ���B����ɁA�V�����_�[�A�s�X�g���A�M������̔M�e�ʂƂ��߂�ꂽ�t�̂̏����͖����ł�����̂Ƃ���B�C�̒萔��R�Ƃ��āA�ȉ��̖�ɓ�����B
[A]�@�͂��߁A�}��(i)�̂悤�Ƀs�X�g���㕔�ɉt�̂͂Ȃ��A�V�����_�[���̋C�̂̈��͂�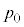 �C�̐ς�
�C�̐ς�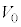 �C���x��
�C���x��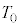 �ł������B���̏�Ԃ����1�Ƃ���B
�ł������B���̏�Ԃ����1�Ƃ���B
�M��������쓮�������Ƀs�X�g���㕔�ɂ���ʂ̉t�̂�Â��ɒ��������Ƃ���A�t�̂̏d���ɂ���ăs�X�g���͂������Ɖ�����A�}��(ii)�̂悤�ɉt�ʂ͔r�o���̉����ɂƂǂ܂����B���̂Ƃ��C�̂̈��͂�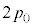 �ł������B���̏�Ԃ����2�Ƃ���B
�ł������B���̏�Ԃ����2�Ƃ���B
���2����M��������쓮�����ċC�̂��������Ɩc�������A�̐ς�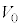 �ɂ����Ƃ���A�t�͔̂r�o�����痬�o���邱�Ƃ͂Ȃ��A�}��(iii)�̂悤�ɉt�ʂ����傤�ǔr�o���̉��[�ɒB�����B���̏�Ԃ����3�Ƃ���B
�ɂ����Ƃ���A�t�͔̂r�o�����痬�o���邱�Ƃ͂Ȃ��A�}��(iii)�̂悤�ɉt�ʂ����傤�ǔr�o���̉��[�ɒB�����B���̏�Ԃ����3�Ƃ���B
(a) ���2�̋C�̂̑̐�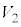 ���A
���A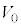 ��p���ĕ\���B�܂��A���2�̋C�̂̉��x
��p���ĕ\���B�܂��A���2�̋C�̂̉��x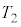 ���A
���A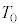 ��p���ĕ\���B
��p���ĕ\���B
(b) ���3�̋C�̂̉��x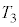 ���A
���A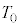 ��p���ĕ\���B
��p���ĕ\���B
(c) ���1������2���o�ď��3�ɕω�����܂łɋC�̂��z�������M��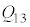 ��R�C
��R�C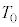 ��p���ĕ\���B�������A�M���z�������ꍇ��
��p���ĕ\���B�������A�M���z�������ꍇ��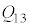 �͐��A���o�����ꍇ�͕��ł���Ƃ���B
�͐��A���o�����ꍇ�͕��ł���Ƃ���B
[B]�@���3������������M��������쓮�����ċC�̂��������Ɩc�������A�r�o������t�̂����ׂĔr�o����ƁA�}��(iv)�̂悤�ɋC�̂̑̐ς�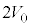 �ƂȂ�A���͂͑�C���Ɠ������Ȃ����B���̏�Ԃ����4�Ƃ���B
�ƂȂ�A���͂͑�C���Ɠ������Ȃ����B���̏�Ԃ����4�Ƃ���B
(d) ���3������4�ɕω�����Ƃ��́A���͂Ƒ̐ς̕ω��̗l�q�ėp����p-V�}�Ɏ����B
���3������4�ɕω�����r���̂����Ԃ�A�Ƃ��A���A�̋C�̂̈��͂�p�C�̐ς�V�C���x��T�Ƃ���B
(e) ���3������A�ɕω�����܂łɋC�̂��z�������M��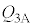 �́A
�́A �ƕ\����B�������A�M���z�������ꍇ��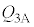 �͐��A���o�����ꍇ�͕��ł���Ƃ���B��(�A)�`(�E)�ɓ��Ă͂܂鐔����
�͐��A���o�����ꍇ�͕��ł���Ƃ���B��(�A)�`(�E)�ɓ��Ă͂܂鐔����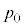 �C
�C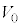 �̂����K�v�Ȃ��̂�p���ĕ\���B
�̂����K�v�Ȃ��̂�p���ĕ\���B
(f) ���A�̋C�̂̉��xT�́A
�ƕ\����B��(�G)�`(�J)�ɓ��Ă͂܂鐔����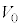 �C
�C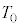 �̂����K�v�Ȃ��̂�p���ĕ\���B
�̂����K�v�Ȃ��̂�p���ĕ\���B
(g) ���3������4�ɕω�����ԂɒB����C�̂̍ō����x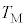 ���A
���A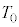 ��p���ĕ\���B
��p���ĕ\���B
(h) ���3������4�ɕω�����Ԃɂ�����B������A���3������B�܂ł͋C�͔̂M���z�����A���B������4�܂ł͋C�͔̂M����o����B���B�̋C�̂̑̐�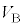 ���A
���A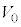 ��p���ĕ\���B
��p���ĕ\���B [��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B