���H�啨��'22�N�O��[3]
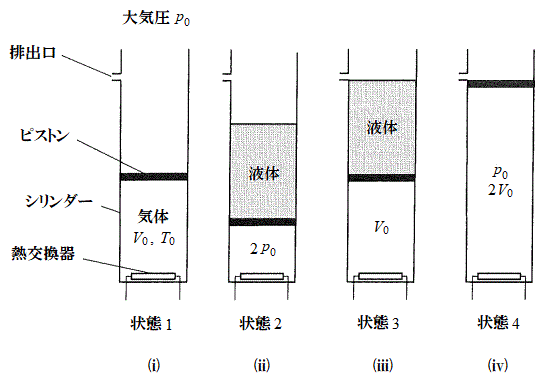 �}�̂悤�ɉ��������Ɋ��炩�ɓ����s�X�g���������V�����_�[�ɁA1�����̒P���q���q���z�C�̂������߂��Ă���B�s�X�g���̏㕔�ɂ͉t�̂����߂���悤�ɂȂ��Ă���B�܂��A�V�����_�[�ɂ̓s�X�g���̏���̈ʒu�ɉt�̂̔r�o�����J�����Ă���B�V�����_�[�͑�C���ɒu����A��C���͏��
�}�̂悤�ɉ��������Ɋ��炩�ɓ����s�X�g���������V�����_�[�ɁA1�����̒P���q���q���z�C�̂������߂��Ă���B�s�X�g���̏㕔�ɂ͉t�̂����߂���悤�ɂȂ��Ă���B�܂��A�V�����_�[�ɂ̓s�X�g���̏���̈ʒu�ɉt�̂̔r�o�����J�����Ă���B�V�����_�[�͑�C���ɒu����A��C���͏��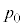 �ł���Ƃ���B�V�����_�[�����ɂ̓V�����_�[���̋C�̂����M�܂��͗�p�ł���M�����킪�ݒu����Ă���B�V�����_�[�ƃs�X�g���͒f�M�ނłł��Ă���A�s�X�g���̎��ʂ���݂͖����ł�����̂Ƃ���B����ɁA�V�����_�[�A�s�X�g���A�M������̔M�e�ʂƂ��߂�ꂽ�t�̂̏����͖����ł�����̂Ƃ���B�C�̒萔��R�Ƃ��āA�ȉ��̖�ɓ�����B
�ł���Ƃ���B�V�����_�[�����ɂ̓V�����_�[���̋C�̂����M�܂��͗�p�ł���M�����킪�ݒu����Ă���B�V�����_�[�ƃs�X�g���͒f�M�ނłł��Ă���A�s�X�g���̎��ʂ���݂͖����ł�����̂Ƃ���B����ɁA�V�����_�[�A�s�X�g���A�M������̔M�e�ʂƂ��߂�ꂽ�t�̂̏����͖����ł�����̂Ƃ���B�C�̒萔��R�Ƃ��āA�ȉ��̖�ɓ�����B
[A]�@�͂��߁A�}��(i)�̂悤�Ƀs�X�g���㕔�ɉt�̂͂Ȃ��A�V�����_�[���̋C�̂̈��͂�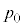 �C�̐ς�
�C�̐ς�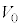 �C���x��
�C���x��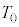 �ł������B���̏�Ԃ����1�Ƃ���B
�ł������B���̏�Ԃ����1�Ƃ���B �M��������쓮�������Ƀs�X�g���㕔�ɂ���ʂ̉t�̂�Â��ɒ��������Ƃ���A�t�̂̏d���ɂ���ăs�X�g���͂������Ɖ�����A�}��(ii)�̂悤�ɉt�ʂ͔r�o���̉����ɂƂǂ܂����B���̂Ƃ��C�̂̈��͂�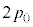 �ł������B���̏�Ԃ����2�Ƃ���B
�ł������B���̏�Ԃ����2�Ƃ���B
���2����M��������쓮�����ċC�̂��������Ɩc�������A�̐ς�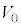 �ɂ����Ƃ���A�t�͔̂r�o�����痬�o���邱�Ƃ͂Ȃ��A�}��(iii)�̂悤�ɉt�ʂ����傤�ǔr�o���̉��[�ɒB�����B���̏�Ԃ����3�Ƃ���B
�ɂ����Ƃ���A�t�͔̂r�o�����痬�o���邱�Ƃ͂Ȃ��A�}��(iii)�̂悤�ɉt�ʂ����傤�ǔr�o���̉��[�ɒB�����B���̏�Ԃ����3�Ƃ���B
(a) ���2�̋C�̂̑̐�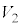 ���A
���A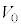 ��p���ĕ\���B�܂��A���2�̋C�̂̉��x
��p���ĕ\���B�܂��A���2�̋C�̂̉��x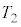 ���A
���A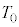 ��p���ĕ\���B
��p���ĕ\���B
(b) ���3�̋C�̂̉��x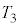 ���A
���A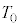 ��p���ĕ\���B
��p���ĕ\���B
(c) ���1������2���o�ď��3�ɕω�����܂łɋC�̂��z�������M��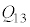 ��R�C
��R�C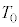 ��p���ĕ\���B�������A�M���z�������ꍇ��
��p���ĕ\���B�������A�M���z�������ꍇ��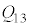 �͐��A���o�����ꍇ�͕��ł���Ƃ���B
�͐��A���o�����ꍇ�͕��ł���Ƃ���B
[B]�@���3������������M��������쓮�����ċC�̂��������Ɩc�������A�r�o������t�̂����ׂĔr�o����ƁA�}��(iv)�̂悤�ɋC�̂̑̐ς�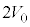 �ƂȂ�A���͂͑�C���Ɠ������Ȃ����B���̏�Ԃ����4�Ƃ���B
�ƂȂ�A���͂͑�C���Ɠ������Ȃ����B���̏�Ԃ����4�Ƃ���B
(d) ���3������4�ɕω�����Ƃ��́A���͂Ƒ̐ς̕ω��̗l�q�ėp����p-V�}�Ɏ����B
���3������4�ɕω�����r���̂����Ԃ�A�Ƃ��A���A�̋C�̂̈��͂�p�C�̐ς�V�C���x��T�Ƃ���B
(e) ���3������A�ɕω�����܂łɋC�̂��z�������M��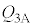 �́A
�́A �ƕ\����B�������A�M���z�������ꍇ��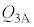 �͐��A���o�����ꍇ�͕��ł���Ƃ���B��(�A)�`(�E)�ɓ��Ă͂܂鐔����
�͐��A���o�����ꍇ�͕��ł���Ƃ���B��(�A)�`(�E)�ɓ��Ă͂܂鐔����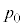 �C
�C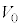 �̂����K�v�Ȃ��̂�p���ĕ\���B
�̂����K�v�Ȃ��̂�p���ĕ\���B
(f) ���A�̋C�̂̉��xT�́A
�ƕ\����B��(�G)�`(�J)�ɓ��Ă͂܂鐔����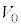 �C
�C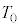 �̂����K�v�Ȃ��̂�p���ĕ\���B
�̂����K�v�Ȃ��̂�p���ĕ\���B
(g) ���3������4�ɕω�����ԂɒB����C�̂̍ō����x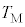 ���A
���A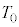 ��p���ĕ\���B
��p���ĕ\���B
(h) ���3������4�ɕω�����Ԃɂ�����B������A���3������B�܂ł͋C�͔̂M���z�����A���B������4�܂ł͋C�͔̂M����o����B���B�̋C�̂̑̐�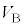 ���A
���A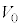 ��p���ĕ\���B
��p���ĕ\���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���܂茩�Ȃ��̖��ł����A��C�o�l�Ɠ������������܂��B�㔼�͂Ђ�����v�Z�ő̗͂�����܂��B
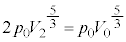 �@��
�@�� 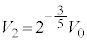 ......[��]
......[��]�A���@���A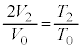 �@��
�@�� 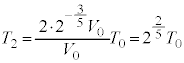 ......[��]
......[��]
(b) ���2�����3�͉t�̂ɓ����d�́{��C�����ω����Ȃ��̂ŁA�C�̂̈��͂��ω������A�舳�ω��ŁA���3�̋C�̂̈��͂�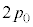 �ł��B
�ł��B ���3����ԕ������F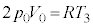 �@����B
�@����B
�B���@���A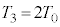 ......[��]
......[��]
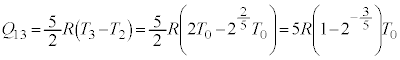 ......[��]
......[��]
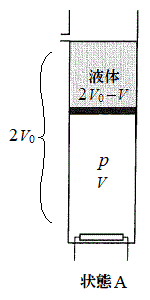 [B](d) �C�̂̑̐ς͏��3��
[B](d) �C�̂̑̐ς͏��3��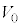 �C���4��
�C���4��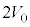 �Ȃ̂ŁA��蕶�̐}����A���3�ł͉t�̂̑̐ς�
�Ȃ̂ŁA��蕶�̐}����A���3�ł͉t�̂̑̐ς�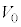 �ł��B�܂��A���3������4�Ɏ���r���̏��A���l���܂��B���A�ɂ����鈳�́A�̐ρA���x��p�CV�CT�Ƃ���ƁA���A�̏�ԕ������F
�ł��B�܂��A���3������4�Ɏ���r���̏��A���l���܂��B���A�ɂ����鈳�́A�̐ρA���x��p�CV�CT�Ƃ���ƁA���A�̏�ԕ������F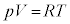 �@����C
�@����C�s�X�g���̒f�ʐς�S�Ƃ���ƁA���A�ɂ����ăs�X�g���ɓ����͂́A�C�̂��s�X�g���������グ���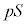 �C��C���������������
�C��C���������������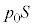 �C�t�̂̑̐ς�
�C�t�̂̑̐ς�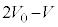 �Ȃ̂ŁA�t�̖̂��x��ρ�C�d�͉����x��
�Ȃ̂ŁA�t�̖̂��x��ρ�C�d�͉����x��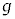 �Ƃ���ƁA�t�̂ɓ����d�͂�
�Ƃ���ƁA�t�̂ɓ����d�͂�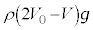 �C�s�X�g�����ɂ߂Ă������Ɠ����x�^������(�����x0)�Ƃ��āA�s�X�g���ɓ����͂̂荇�����A
�C�s�X�g�����ɂ߂Ă������Ɠ����x�^������(�����x0)�Ƃ��āA�s�X�g���ɓ����͂̂荇�����A 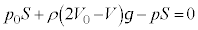 �@����D
�@����D���3�ɂ����āA�s�X�g���ɓ����͂̂荇�����A 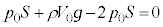 �@��
�@�� 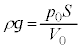
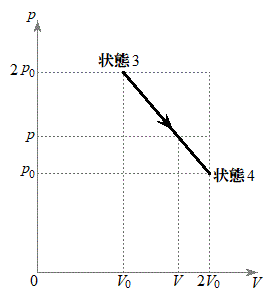 �D�ɑ�����āA
�D�ɑ�����āA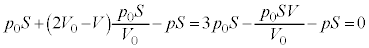 ��
�� 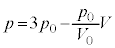 �@����E
�@����E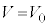 �̂Ƃ�(���3)
�̂Ƃ�(���3)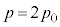 �C
�C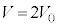 �̂Ƃ�(���4)
�̂Ƃ�(���4)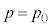 ���Ap-V�}�͒����ʼnE�}����(�����I�ω����Q��)�B
���Ap-V�}�͒����ʼnE�}����(�����I�ω����Q��)�B
�E���A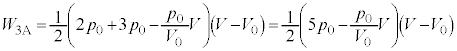
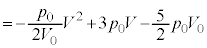 �@����F
�@����F�E���C�ɑ�����āA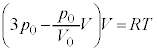
�� 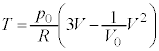 �@����G
�@����G ����āA�M�͊w���@�����A���3�����A�ŋC�̂��z�������M��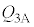 �́A
�́A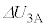 �ɇF�������āA
�ɇF�������āA 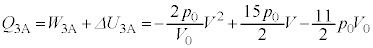 �@����H
�@����H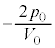 ......[�A]�C�@
......[�A]�C�@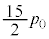 ......[�C]�C�@
......[�C]�C�@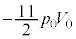 ......[�E]
......[�E]
(f) �G�Ň@���g����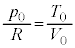 ���A
���A 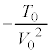 ......[�G]�C�@
......[�G]�C�@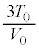 ......[�I]�C�@0 ......[�J]
......[�I]�C�@0 ......[�J]
(g) (f)�̌��ʂ��A
������A���xT�́A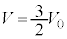 (
(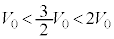 )�̂Ƃ��A�ő�l
)�̂Ƃ��A�ő�l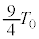 ���Ƃ�܂�(2�����̍ő�E�ŏ����Q��)�B����āA
���Ƃ�܂�(2�����̍ő�E�ŏ����Q��)�B����āA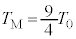 ......[��]
......[��]
(h) ���3������B�܂ŋC�̂��M���z�����A���B������4�܂ŋC�̂��M����o����A�Ƃ������Ƃ́A�C�̂��z�������M��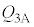 �����B�ɂ����čő�ɂȂ�A�Ƃ������Ƃł��B�H���A
�����B�ɂ����čő�ɂȂ�A�Ƃ������Ƃł��B�H���A ����āA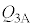 ��
��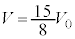 (
(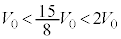 )�̂Ƃ��ő�ŁA
)�̂Ƃ��ő�ŁA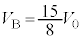 ......[��]
......[��] ���D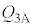 ��V��2�����ŁA
��V��2�����ŁA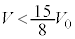 �ő����A
�ő����A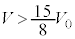 �Ō����ł��B��������ԁA�C�͔̂M���z�����A�����ɓ]����ƁA�C�͔̂M����o���܂��B
�Ō����ł��B��������ԁA�C�͔̂M���z�����A�����ɓ]����ƁA�C�͔̂M����o���܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 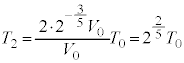 ......[��]
......[��]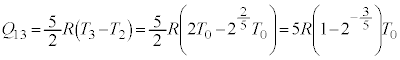 ......[��]
......[��]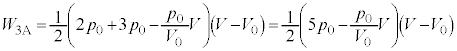
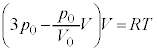
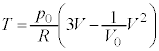 �@����G
�@����G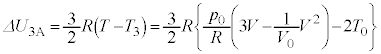
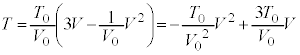
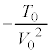 ......[�G]�C�@
......[�G]�C�@