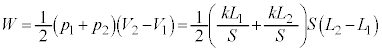�����I�ω��@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
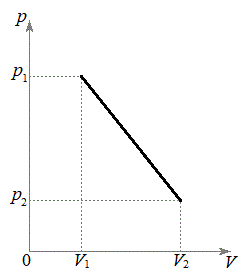 ����p���̐�V��1�����ŕ\����ω�������B
����p���̐�V��1�����ŕ\����ω�������B
���A (����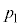 �C�̐�
�C�̐�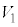 )������B (����
)������B (����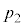 �C�̐�
�C�̐�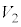 )�ֈڂ�ߒ���������p�C�̐�V�́A
)�ֈڂ�ߒ���������p�C�̐�V�́A
�ƂȂ�A����́Ap-V�}��ŁA2�_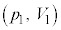 �C
�C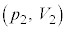 ��ʂ������̕������B
��ʂ������̕������B
���A������B�Ɉڂ�ߒ��ŁA�C�̂��O���ɂ����d��W�́Ap-V�}��̑�`�̖ʐςƂ��āA
�ŗ^������B
���z�C���̏�ԕω��Ƃ��āA���ȏ��ɂ́A�舳�ω��A��ϕω��A�����ω��A�f�M�ω���4�ʂ�̕ω��̐�����������Ă��܂����A�����ł́A������A�u�����I�ω��v�Ƃł��ĂԂׂ��ω����o�肳��܂��B
���̕ω��́A��L�̃O���t�̂悤�ɁApV�}�������ɂȂ�̂ł����A���A (����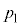 �C�̐�
�C�̐�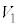 )������B (����
)������B (����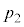 �C�̐�
�C�̐�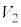 )�ֈڂ�ߒ����C�̂̂����d������`�̖ʐςƂ��ėe�Ղɋ��߂���̂œ����ł����グ���܂��B
)�ֈڂ�ߒ����C�̂̂����d������`�̖ʐςƂ��ėe�Ղɋ��߂���̂œ����ł����グ���܂��B
�C�̂������I�ω�������̂́A(i)�V�����_�[���ɋC�̂�����߂Ă���s�X�g���Ƀo�l�����Ă�����ƁA(ii)�o�l�����Ă��Ȃ��Ă��s�X�g���̏�ɂ����肪����Ă�����ł��B
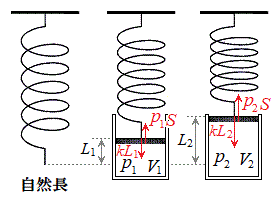 (i) �s�X�g���Ƀo�l�����Ă�����
(i) �s�X�g���Ƀo�l�����Ă������E�}�̂悤�ɁA�ʐ�S�̃s�X�g���Ƀo�l�����Ă���ꍇ�A�C�̂�������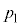 �C�̐���
�C�̐���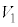 �̏��A����A�C�̂��M�������āA������
�̏��A����A�C�̂��M�������āA������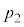 �C�̐���
�C�̐���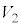 �̏��B�ɕω������Ƃ��܂��B�ω��r����������p�C�̐���V�Ƃ���(���̏�Ԃ�C�Ƃ��܂�)�ƁA���A�Ńo�l���k����
�̏��B�ɕω������Ƃ��܂��B�ω��r����������p�C�̐���V�Ƃ���(���̏�Ԃ�C�Ƃ��܂�)�ƁA���A�Ńo�l���k����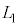 �Ƃ��āA�s�X�g���ɓ����͂̂荇�����A
�Ƃ��āA�s�X�g���ɓ����͂̂荇�����A 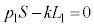 �@����@
�@����@���C�Ńo�l���k����L�Ƃ��āA�s�X�g���ɓ������̂荇�����A
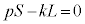 �@����A
�@����A�@�|�A���A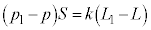 �@����B
�@����B
�Ƃ���ŁA���̊Ԃ̋C�̂��̐��ω��ɂ��āA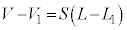 �@����C
�@����C
�B�C�C���A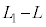 ����������ƁA
����������ƁA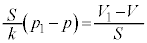
���@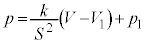
������A���A������B�̉ߒ��ɂ����āApV�}�������ɂȂ邱�Ƃ��킩��܂��B���B�ɂ����āA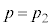 �̂Ƃ��A
�̂Ƃ��A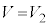 �Ȃ̂ŁA�����̌X���́A
�Ȃ̂ŁA�����̌X���́A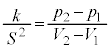 �ƂȂ�܂��B���B�ł˂��k����
�ƂȂ�܂��B���B�ł˂��k����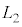 �Ƃ��āA�@���A
�Ƃ��āA�@���A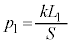 �C�A��
�C�A��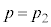 �C
�C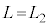 �Ƃ��āA
�Ƃ��āA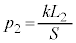 �C�C��
�C�C��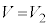 �̂Ƃ���
�̂Ƃ���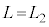 �ƂȂ�̂ŁA�C�̂̂����d���́A
�ƂȂ�̂ŁA�C�̂̂����d���́A ����́A���A������B�ɕω�����Ƃ��̃o�l���e���G�l���M�[�̕ω��ł��B�܂�A�C�̂̂����d���̓o�l���e���G�l���M�[�̑������ɂȂ�킯�ł��B
(ii) �s�X�g���̏�ɂ����肪����Ă�����
�c�ɒu���ꂽ�V�����_�[�ɋC�̂����������������ł����ʐ�S�̃s�X�g���łӂ������܂��B�s�X�g���̏������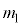 �̂������u���A�C�̂�����
�̂������u���A�C�̂�����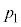 �C�̐�
�C�̐�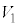 �̏��A����A�C�̂����M���邩������ω������āA�C�̂̏�Ԃ�ω������A���̉ߒ��ɂ�����A������p�C�̐���V�C�������������m�Ƃ���ƁA�s�X�g���ɂ͑�C��
�̏��A����A�C�̂����M���邩������ω������āA�C�̂̏�Ԃ�ω������A���̉ߒ��ɂ�����A������p�C�̐���V�C�������������m�Ƃ���ƁA�s�X�g���ɂ͑�C��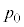 �������A�s�X�g���ɓ������̂荇�����A
�������A�s�X�g���ɓ������̂荇�����A 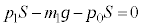 �@����@
�@����@
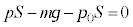 �@����A
�@����A�@�|�A���A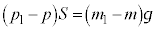 �@����B
�@����B
�����������m���A�C�̂��̐�V�ɑ��āA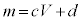 (c�Cd�F�萔)�ƂȂ�悤�ɕω�������ƁA
(c�Cd�F�萔)�ƂȂ�悤�ɕω�������ƁA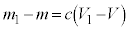 �C������B�ɑ�����āA
�C������B�ɑ�����āA 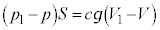 �@��
�@�� 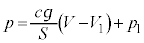
���̂Ƃ����ApV�}�͒����ɂȂ�܂��B�C�̂��o�l�̂悤�ȓ��������܂��B
(i)�C(ii)�Ƃ��A�o�l���e�����A��������d�����A�V�����_�[���̋C�̂������ɔ�Ⴗ�邱�Ƃ��|�C���g�ł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@������b����TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B