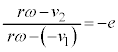���H�啨��'22�N�O��[1]
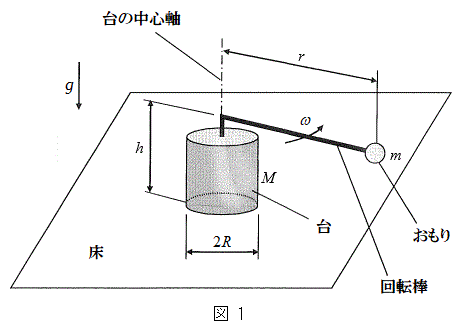 �}1�̂悤�ɁA���a
�}1�̂悤�ɁA���a �̉~���`�̑�ƁA���̑�Ɏx������A��̒�ʂ���h�̍����̕��ʓ����̒��S������ɉ�]���钷��r (
�̉~���`�̑�ƁA���̑�Ɏx������A��̒�ʂ���h�̍����̕��ʓ����̒��S������ɉ�]���钷��r ( )�̉�]�_�ƁA���̉�]�_�̐�[�ɌŒ肳�ꂽ�傫���������ł��鎿��m�̂����肩��Ȃ鑕�u���A�����ȏ��̏�ɒu����Ă���B���̑�̓����ɂ̓��[�^�[������A�ォ�猩�Ĕ����v���ɉ�]�_����]�����邱�Ƃ��ł���B��]�_�̊p���xω�͎��R�ɕς��邱�Ƃ��ł���B���[�^�[���܂߂���̎��ʂ�M�ł���A���̏d�S�͑�̒��S����ɂ���B��]�_�͕ό`�����A���̎��ʂ͖����ł�����̂Ƃ���B�܂��A��C��R�͖����ł�����̂Ƃ���B�d�͉����x��
)�̉�]�_�ƁA���̉�]�_�̐�[�ɌŒ肳�ꂽ�傫���������ł��鎿��m�̂����肩��Ȃ鑕�u���A�����ȏ��̏�ɒu����Ă���B���̑�̓����ɂ̓��[�^�[������A�ォ�猩�Ĕ����v���ɉ�]�_����]�����邱�Ƃ��ł���B��]�_�̊p���xω�͎��R�ɕς��邱�Ƃ��ł���B���[�^�[���܂߂���̎��ʂ�M�ł���A���̏d�S�͑�̒��S����ɂ���B��]�_�͕ό`�����A���̎��ʂ͖����ł�����̂Ƃ���B�܂��A��C��R�͖����ł�����̂Ƃ���B�d�͉����x�� �Ƃ���B
�Ƃ���B
[A]�@��Ə��̊Ԃ̐Î~���C�W����μ�Ƃ���BR�Cr�Ch�CM�Cm�Cμ���قȂ镡���̑��u�����A���̏�ɒu���āA��]�_����ё䂪�Î~������Ԃ����]�_�̊p���x���������Ƒ傫�����Ă������B����ƁA���u�̈Ⴂ�ɂ���ĉ��L��2�̏ꍇ�����邱�Ƃ��킩�����B
�y�T�z�@�䂪�X�����ƂȂ���]�_�̕����ɏ��̏������n�߂�
�y�U�z�@�䂪���̏�����邱�ƂȂ���]�_�̕����ɌX���n�߂�
�������A�y�T�z�C�y�U�z���N����O�ɁA�䂪���ɑ��ĉ�]���邱�Ƃ͂Ȃ������B�ȉ��̖�ɓ�����B
(a) ��]�_����]���Ă��Ȃ��Ƃ��A�䂪�|��Ȃ����߂ɂ́A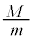 ������l�ȏ�łȂ���Ȃ�Ȃ��B���̏��������L�̎��ŕ\���Ƃ��A��(�A)�ɓ���K�Ȑ�����R��r��p���ĕ\���B
������l�ȏ�łȂ���Ȃ�Ȃ��B���̏��������L�̎��ŕ\���Ƃ��A��(�A)�ɓ���K�Ȑ�����R��r��p���ĕ\���B
(b) �y�T�z���N����ꍇ�A�䂪���̏������n�߂�Ƃ��̉�]�_�̊p���x ��r�CM�Cm�Cμ�C
��r�CM�Cm�Cμ�C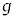 ��p���ĕ\���B
��p���ĕ\���B
(c) �y�U�z���N����ꍇ�A�䂪�X���n�߂�Ƃ��̉�]�_�̊p���x ��R�Cr�Ch�CM�Cm�C
��R�Cr�Ch�CM�Cm�C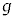 ��p���ĕ\���B
��p���ĕ\���B
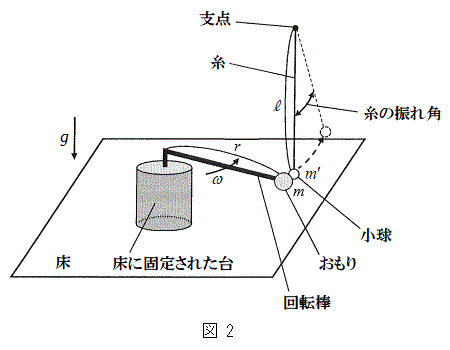 [B]�@������̏�ɌŒ肵�A���[�^�[�ɂ���]�_�����̊p���xω�ʼn�]�����Ă����B���[�^�[�͏[�����͂ŁA������͏�ɓ����~�^���𑱂�����̂Ƃ���B���̏�Ԃɂ����āA�}2�̂悤�ɁA����
[B]�@������̏�ɌŒ肵�A���[�^�[�ɂ���]�_�����̊p���xω�ʼn�]�����Ă����B���[�^�[�͏[�����͂ŁA������͏�ɓ����~�^���𑱂�����̂Ƃ���B���̏�Ԃɂ����āA�}2�̂悤�ɁA���� �̎��Ƒ傫���������ł��鎿��
�̎��Ƒ傫���������ł��鎿�� �̏�������Ȃ�U��q���������~�낵�Ă����A�����肪�ʂ�~�O����ɏ�����Î~�������B���̌�A�U��q�̎x�_(�����Ƃ͋t���̎��̒[)�̈ʒu�͕ς��Ȃ����̂Ƃ���B
�̏�������Ȃ�U��q���������~�낵�Ă����A�����肪�ʂ�~�O����ɏ�����Î~�������B���̌�A�U��q�̎x�_(�����Ƃ͋t���̎��̒[)�̈ʒu�͕ς��Ȃ����̂Ƃ���B����ƁA������Ə������Փ˂��A�����͏Փˎ��̂�����̐i�s�����ɑ��� �œ����o�����B���̌�A�����͒P�U��q�̉^�����s���A�B�ĂяՓ˒n�_�܂ō~��Ă����B���̊ԁA��]�_�͑�̎����������āA������Ə�����1��ڂ̏Փ˂Ɠ����ʒu��2��ڂ̏Փ˂��s���A�����͏Փˎ��̂�����̐i�s�����ɑ���
�œ����o�����B���̌�A�����͒P�U��q�̉^�����s���A�B�ĂяՓ˒n�_�܂ō~��Ă����B���̊ԁA��]�_�͑�̎����������āA������Ə�����1��ڂ̏Փ˂Ɠ����ʒu��2��ڂ̏Փ˂��s���A�����͏Փˎ��̂�����̐i�s�����ɑ��� �œ����o�����B�����Ƃ�����̊Ԃ̔����W����e�Ƃ���B
�œ����o�����B�����Ƃ�����̊Ԃ̔����W����e�Ƃ���B
����2��Փ˂̎�����r�C �Ce�Cm�C
�Ce�Cm�C ���قȂ镡���̑��u�ƐU��q��p���čs�����B�������A��L�̏Փ˂��N����悤�ɁA���ꂼ��̑��u�ƐU��q�ɂ����ĉ�]�_�̊p���xω��K�ɐݒ肵���B���͐L�т��A���̎��ʂ͖����ł�����̂Ƃ���B�܂��A���̐U��p(�����������ƂȂ��p)��
���قȂ镡���̑��u�ƐU��q��p���čs�����B�������A��L�̏Փ˂��N����悤�ɁA���ꂼ��̑��u�ƐU��q�ɂ����ĉ�]�_�̊p���xω��K�ɐݒ肵���B���͐L�т��A���̎��ʂ͖����ł�����̂Ƃ���B�܂��A���̐U��p(�����������ƂȂ��p)�� ���邱�Ƃ͂Ȃ����̂Ƃ���B�ȉ��̖�ɓ�����B
���邱�Ƃ͂Ȃ����̂Ƃ���B�ȉ��̖�ɓ�����B
(d) 1��ڂ̏Փ˒���̏����̑��� ��2��ڂ̏Փ˒���̏����̑���
��2��ڂ̏Փ˒���̏����̑���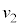 ��r�Ce�Cω��p���Ă��ꂼ��\���B
��r�Ce�Cω��p���Ă��ꂼ��\���B
(e) ���鑕�u�ƐU��q��p���Ď������s�����Ƃ���A���̐U��p�͏[���ɏ����������B���̂Ƃ��A�����̉^����P�U���Ƃ݂Ȃ����Ƃɂ��A��]�_�̊p���xω�� ��
�� ��p���ĕ\���B
��p���ĕ\���B 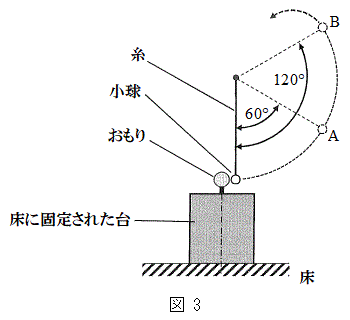 (f) �O��(e)�Ƃ͈قȂ鑕�u�ƐU��q��p���Ď������s�����Ƃ���A���̐U��p�͑傫���Ȃ����B�}3�́A���̎����ɂ����鏬���̉^���̗l�q���A�������������ʂɑ������ȕ������猩���}�ł���B1��ڂ̏Փˌ�A�����͎��̐U��p��
(f) �O��(e)�Ƃ͈قȂ鑕�u�ƐU��q��p���Ď������s�����Ƃ���A���̐U��p�͑傫���Ȃ����B�}3�́A���̎����ɂ����鏬���̉^���̗l�q���A�������������ʂɑ������ȕ������猩���}�ł���B1��ڂ̏Փˌ�A�����͎��̐U��p�� �ƂȂ�ʒuA�ōō��_�ɒB�����B���̂��Ƃ���A1��ڂ̏Փ˒���̏����̑���
�ƂȂ�ʒuA�ōō��_�ɒB�����B���̂��Ƃ���A1��ڂ̏Փ˒���̏����̑���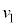 ��
��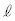 ��
��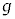 ��p���ĕ\���B
��p���ĕ\���B
(g) �O��(f)�̎����ɂ����āA2��ڂ̏Փˌ�A�����͎��̐U��p��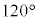 �ƂȂ�ʒuB�ɒB�����B�ʒuB�ɏ������B����܂Ŏ��͂���܂Ȃ��������A�������ʒuB�ɒB�������ォ�玅�͂���݁A�����͕����^�����n�߂��B���̂��Ƃ���A2��ڂ̏Փ˒���̏����̑���
�ƂȂ�ʒuB�ɒB�����B�ʒuB�ɏ������B����܂Ŏ��͂���܂Ȃ��������A�������ʒuB�ɒB�������ォ�玅�͂���݁A�����͕����^�����n�߂��B���̂��Ƃ���A2��ڂ̏Փ˒���̏����̑���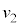 ��
�� ��
�� ��p���ĕ\���B
��p���ĕ\���B
(h) ��(d)�C(f)�C(g)�̌��ʂ𗘗p���āA��(f)�����(g)�̎����ɂ����鏬���Ƃ�����̊Ԃ̔����W��e�̒l�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@������Ȃ��������܂����A���H��Ƃ��ẮA���L����b������₤���e�ɂȂ��Ă��܂��B[B]�ŁA���[�^�[�����͂ŏՓ˂��Ă������~�^�����ێ������A�Ƃ����ݒ�́A�Փ˂̏u�Ԃɓ����~�^�����ێ����邽�߂̊O�͂��ڐ������ɓ����A�Ƃ������Ƃ��Ӗ����Ă��āA�ՓˑO��ʼn^���ʕۑ����������Ȃ����Ƃɒ��ӂ��Ă��������B
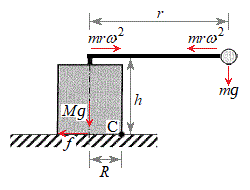 [A](a) �E�}��C�_(�~����̉��ʒ[�ʼn�]�_�����̓_)�̂܂����͂̃��[�����g���l���܂�(��]���Ă��Ȃ��̂�
[A](a) �E�}��C�_(�~����̉��ʒ[�ʼn�]�_�����̓_)�̂܂����͂̃��[�����g���l���܂�(��]���Ă��Ȃ��̂� �ł�)�B�����v���̃��[�����g�́A��̏d�͂ɂ�郂�[�����g
�ł�)�B�����v���̃��[�����g�́A��̏d�͂ɂ�郂�[�����g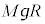 �C���v���̃��[�����g�́A������̏d�͂ɂ�郂�[�����g
�C���v���̃��[�����g�́A������̏d�͂ɂ�郂�[�����g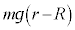 �ł��B�䂪�|��Ȃ��Ƃ���C�_�̂܂����͂̃��[�����g�̂荇���́A
�ł��B�䂪�|��Ȃ��Ƃ���C�_�̂܂����͂̃��[�����g�̂荇���́A �@��
�@�� 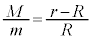
�䂪�|��Ȃ��Ƃ��A�����v���̃��[�����g�̕����傫���A
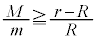 ......[�A]
......[�A]
(b) ����n�߂�Ƃ����l���܂��B���̂Ƃ�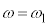 �ŁA�����肪��]�_�������S�͂͑�̒��S��������
�ŁA�����肪��]�_�������S�͂͑�̒��S��������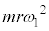 �C��]�_�ɂ͂��������p�ƂȂ�O�����̗͂������A��]�_���~���̒��a�����Ɉړ����Ȃ����߂ɁA���̗͂Ƃ荇���͂�������Ƃ͋t�����ɉ�]������܂��B����ƁA�~����͊O����(������̕���)�ɑ傫��
�C��]�_�ɂ͂��������p�ƂȂ�O�����̗͂������A��]�_���~���̒��a�����Ɉړ����Ȃ����߂ɁA���̗͂Ƃ荇���͂�������Ƃ͋t�����ɉ�]������܂��B����ƁA�~����͊O����(������̕���)�ɑ傫��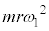 �̗͂��܂��B�~���䂪����Ȃ��̂ŁA��Ə��̊Ԃ��Î~���C����f �Ƃ���ƁA�~����ɓ����͂̂荇���́A
�̗͂��܂��B�~���䂪����Ȃ��̂ŁA��Ə��̊Ԃ��Î~���C����f �Ƃ���ƁA�~����ɓ����͂̂荇���́A �~���䂪������������R����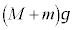 �C����n�߂�Ƃ��Î~���C�͍͂ő�Î~���C�͂ł����āA
�C����n�߂�Ƃ��Î~���C�͍͂ő�Î~���C�͂ł����āA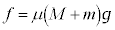
����āA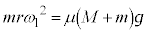 �@��
�@�� 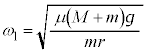 ......[��]
......[��]
(c) �X���n�߂�Ƃ� �ŁA��̒��S���ɂ͊O������
�ŁA��̒��S���ɂ͊O������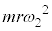 �������AC�_�̂܂��̗͂̃��[�����g�́A�����v����
�������AC�_�̂܂��̗͂̃��[�����g�́A�����v���� �C���v����
�C���v����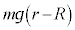 �C
�C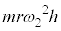 �ł���A�Î~���C�͂̃��[�����g��0 (���ł̒�����0)�ł��B�͂̃��[�����g�̂荇���́A
�ł���A�Î~���C�͂̃��[�����g��0 (���ł̒�����0)�ł��B�͂̃��[�����g�̂荇���́A  �@��
�@�� 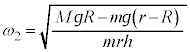 ......[��]
......[��]
1��ڂ̏Փˌ�ɑ��� �ƂȂ��������́A�͊w�I�G�l���M�[�ۑ����2��ڂ̏Փ˒��O��������
�ƂȂ��������́A�͊w�I�G�l���M�[�ۑ����2��ڂ̏Փ˒��O�������� (�����͋t)�ŁA�Փˌ�ɑ���
(�����͋t)�ŁA�Փˌ�ɑ���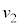 �ɂȂ�܂��B�����W���̎����A
�ɂȂ�܂��B�����W���̎����A
�P�U��q�̔������͉�]�_�̓����~�^����1�����ɂȂ�̂ŁA
 �@��
�@��  ......[��]�@(��蕶�ɁA���̐U��p�͏[���ɏ������A�Ə�����Ă���̂ŁA�P�U��q�Ƃ��čl���܂�)
......[��]�@(��蕶�ɁA���̐U��p�͏[���ɏ������A�Ə�����Ă���̂ŁA�P�U��q�Ƃ��čl���܂�)
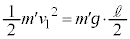 �@��
�@��  ......[��]�@(���̐U��p�������ƌ����Ȃ��̂ŁA�P�U��q�Ƃ��čl���邱�Ƃ͂ł��܂���B�s�����~�^�����Q��)
......[��]�@(���̐U��p�������ƌ����Ȃ��̂ŁA�P�U��q�Ƃ��čl���邱�Ƃ͂ł��܂���B�s�����~�^�����Q��)(g) ���̐U��p��θ�̂Ƃ��̏����̑�����v�C�����ɓ�������������S�Ƃ���ƁA���̂Ƃ��̏d�͂̎��ɉ��������̐����́A�x�_�Ɍ����������𐳂Ƃ��� �C�������^���������́A
�C�������^���������́A 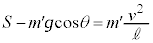 �@����@
�@����@�Փ˒���ƐU��p��θ�̂Ƃ�(�Փ˒���Ƃ̍����̍��� )�A�����̑�����v�Ƃ���ƁA�^���G�l���M�[��
)�A�����̑�����v�Ƃ���ƁA�^���G�l���M�[��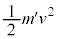 �C�ʒu�G�l���M�[��
�C�ʒu�G�l���M�[��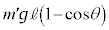 �ł��B�Փ˒���ƐU��p��θ�̂Ƃ��Ƃ��͊w�I�G�l���M�[�ۑ����A
�ł��B�Փ˒���ƐU��p��θ�̂Ƃ��Ƃ��͊w�I�G�l���M�[�ۑ����A  ���@�ɑ������ƁA
���@�ɑ������ƁAB�_��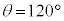 �C����ތ��E(�������Q��)�Ȃ̂�
�C����ތ��E(�������Q��)�Ȃ̂� �Ƃ��āA
�Ƃ��āA
(h) (d)(f)(g)�̌��ʂ��A
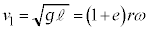 �@����A
�@����A
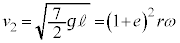 �@����B
�@����B�B���A���A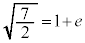 �@��
�@�� 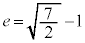 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 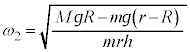 ......[��]
......[��]