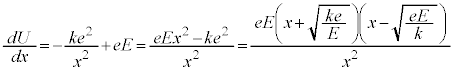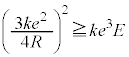���H�啨��'22�N�O��[2]
 N�𐳂̐����Ƃ���B�^�ɂ����āA����
N�𐳂̐����Ƃ���B�^�ɂ����āA����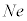 �̐��d�ׂ����aR�̋����Ɉ�l�ɕ��z���A���d��
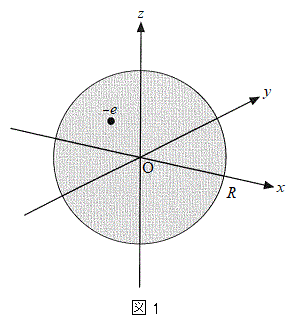
�̐��d�ׂ����aR�̋����Ɉ�l�ɕ��z���A���d��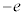 �����דd���q��N�������݂���Ƃ���B���̋��̒��S�����_O�Ƃ��āA�݂��ɒ�������悤��x���Cy���Cz����݂���B���̂Ƃ��A���d�ׂ̕��z�����_���狗��r�������ꂽ�_�ɂ���d��́A���_�𒆐S�Ƃ��锼�ar�̋������̐��d�ׂ��S�Č��_�ɏW�������ƍl�����Ƃ��ɐ�����d��ɓ������A���̊O���̐��d�ׂɂ͂��Ȃ����Ƃ��m���Ă���B�}1�́A
�����דd���q��N�������݂���Ƃ���B���̋��̒��S�����_O�Ƃ��āA�݂��ɒ�������悤��x���Cy���Cz����݂���B���̂Ƃ��A���d�ׂ̕��z�����_���狗��r�������ꂽ�_�ɂ���d��́A���_�𒆐S�Ƃ��锼�ar�̋������̐��d�ׂ��S�Č��_�ɏW�������ƍl�����Ƃ��ɐ�����d��ɓ������A���̊O���̐��d�ׂɂ͂��Ȃ����Ƃ��m���Ă���B�}1�́A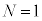 �̏ꍇ�ɁA���d�ׂ̕��z�Ɖדd���q�̈ʒu�̗�����������̂ł���B
�̏ꍇ�ɁA���d�ׂ̕��z�Ɖדd���q�̈ʒu�̗�����������̂ł���B
�דd���q�̎��ʂ�m�C�N�[�����̖@���̔��萔��k�Ƃ��A���d�ׂ̕��z�͕s�ςœ������A�דd���q�ɑ��ĐÓd�C�͈ȊO�̗͂��y�ڂ��Ȃ����̂Ƃ���B�܂��A�d���g�̕��˂�d�͖͂����ł�����̂Ƃ���B
[A]�@�ȉ��̖�ɓ�����B
(a) �ȉ��̕��͒��̋�(�A)�`(�J)�ɓ��Ă͂܂�K�Ȑ������Ae�CR�Cm�Ck�̂����K�v�Ȃ��̂�p���ĕ\���B
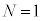 �̏ꍇ�ɁA�דd���q�����_���狗��r�������ꂽ�_�ɑ��݂���Ƃ��A���̉דd���q�����d�ׂ̕��z�����Ód�C�͂̑傫��F�ƁA���̐Ód�C�͂ɂ��דd���q�̈ʒu�G�l���M�[U���l����B�܂��A
�̏ꍇ�ɁA�דd���q�����_���狗��r�������ꂽ�_�ɑ��݂���Ƃ��A���̉דd���q�����d�ׂ̕��z�����Ód�C�͂̑傫��F�ƁA���̐Ód�C�͂ɂ��דd���q�̈ʒu�G�l���M�[U���l����B�܂��A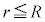 �̏ꍇ�ɂ�����Ód�C�͂͌��_�Ɍ������A���̑傫����
�̏ꍇ�ɂ�����Ód�C�͂͌��_�Ɍ������A���̑傫����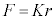 �̂悤��r�ɔ�Ⴕ�A���̔��萔��
�̂悤��r�ɔ�Ⴕ�A���̔��萔��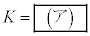 �ł���B�˂ɂ��e���͂Ɠ��l�ɗ͂̑傫����r�ɔ�Ⴗ��̂ŁA�דd���q�̈ʒu�G�l���M�[�́A���_����Ƃ���
�ł���B�˂ɂ��e���͂Ɠ��l�ɗ͂̑傫����r�ɔ�Ⴗ��̂ŁA�דd���q�̈ʒu�G�l���M�[�́A���_����Ƃ���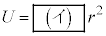 �ƂȂ�B
�ƂȂ�B
����A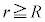 �̏ꍇ�ɂ�����Ód�C�͂����_�Ɍ������A���̑傫����
�̏ꍇ�ɂ�����Ód�C�͂����_�Ɍ������A���̑傫���� �̂悤��r�̓��ɔ���Ⴗ��B����āA�דd���q�̈ʒu�G�l���M�[�́A
�̂悤��r�̓��ɔ���Ⴗ��B����āA�דd���q�̈ʒu�G�l���M�[�́A �ƂȂ�B�����ŁAC��r�ɂ��Ȃ��萔�ł���A
�ƂȂ�B�����ŁAC��r�ɂ��Ȃ��萔�ł���A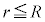 �ɂ�����ʒu�G�l���M�[��
�ɂ�����ʒu�G�l���M�[��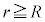 �ɂ�����ʒu�G�l���M�[�Ƃ�
�ɂ�����ʒu�G�l���M�[�Ƃ�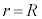 �ɂ����Ĉ�v���邱�Ƃ���A
�ɂ����Ĉ�v���邱�Ƃ���A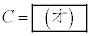 �ƒ�܂�B
�ƒ�܂�B
�ȏ�̌��ʂ�p����ƁA���_�ŐÎ~���Ă���דd���q�����ɂ܂ň����������߂ɕK�v�ƂȂ�ŏ��̎d��W�́A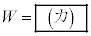 �ƂȂ邱�Ƃ��킩��B
�ƂȂ邱�Ƃ��킩��B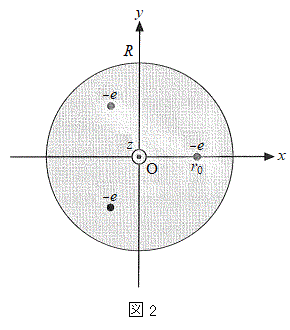 (b)
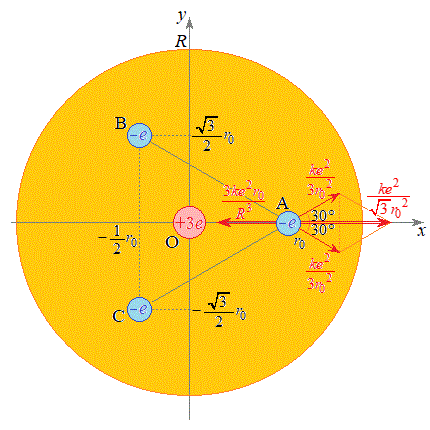
(b) 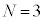 �̏ꍇ�ɁA���aR�̋����ɑ��݂���3�̉דd���q���l����B�}2�̂悤�ɁA����炪
�̏ꍇ�ɁA���aR�̋����ɑ��݂���3�̉דd���q���l����B�}2�̂悤�ɁA����炪 ��x-y���ʓ��ɂ����āA���_���d�S�Ƃ��鐳�O�p�`�̊e���_�ŐÎ~���A�����ł͐Ód�C�͂��荇���B���̂Ƃ��A���d�ׂ̑��ʂ�
��x-y���ʓ��ɂ����āA���_���d�S�Ƃ��鐳�O�p�`�̊e���_�ŐÎ~���A�����ł͐Ód�C�͂��荇���B���̂Ƃ��A���d�ׂ̑��ʂ�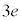 �ł��邱�Ƃɒ��ӂ��āA���_����דd���q�̈ʒu�܂ł̋���
�ł��邱�Ƃɒ��ӂ��āA���_����דd���q�̈ʒu�܂ł̋���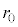 ���Ae�CR�Cm�Ck�̂����K�v�Ȃ��̂�p���ĕ\���B
���Ae�CR�Cm�Ck�̂����K�v�Ȃ��̂�p���ĕ\���B
 [B]�@
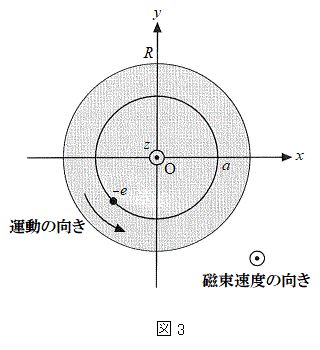
[B]�@ �̏ꍇ�ɁAz���̐��̌����Ɉ��ň�l�Ȏ���������A���̎������x�̑傫����B�Ƃ���B���̂Ƃ��A�}3�̂悤�ɁA
�̏ꍇ�ɁAz���̐��̌����Ɉ��ň�l�Ȏ���������A���̎������x�̑傫����B�Ƃ���B���̂Ƃ��A�}3�̂悤�ɁA ��x-y���ʓ��ɂ����Č��_�𒆐S�Ƃ��锼�aa (
��x-y���ʓ��ɂ����Č��_�𒆐S�Ƃ��锼�aa ( )�̉~�O������~�^������דd���q���l����B�דd���q�̊p���x��ω�Ƃ��A�����~�^���̌�����z���̐��̑����猩�Ĕ����v���ł���Ƃ���B�ȉ��̖�ɓ�����B
)�̉~�O������~�^������דd���q���l����B�דd���q�̊p���x��ω�Ƃ��A�����~�^���̌�����z���̐��̑����猩�Ĕ����v���ł���Ƃ���B�ȉ��̖�ɓ�����B
(c) �דd���q�̊p���xω�����߂�B�������A�{��ł́A[A]�̖�(a)��(�A)�ŋ��߂����萔��K�Ƃ����Ae�Cm�CB�CK�̂����K�v�Ȃ��̂�p���ĕ\���B
(d) �����~�^���̎��������[���ɒ������Ԃɂ킽���ĉ~�O����̂���_��ʉ߂���d�C�ʂς��邱�ƂŁA�~�O����𗬂��d��I�����߁Ae�Cm�Ca�Cω�̂����K�v�Ȃ��̂�p���ĕ\���B�������A�d���̌����������v���̂Ƃ�I�̒l�͐��A���v���̂Ƃ�I�̒l�͕��ƂȂ���̂Ƃ���B
(e) ��(d)�̓d�������_�ɂ��鎥���z���� ���Ae�Cm�Ca�Cω�̂����K�v�Ȃ��̂�p���ĕ\���B
���Ae�Cm�Ca�Cω�̂����K�v�Ȃ��̂�p���ĕ\���B
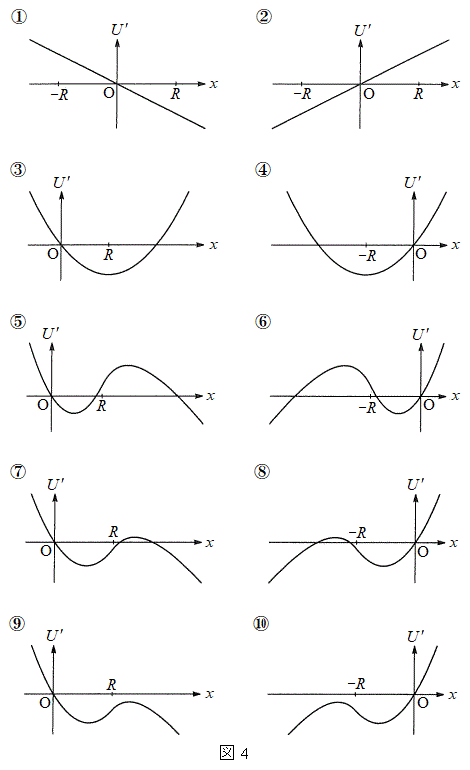 [C]�@
[C]�@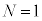 �̏ꍇ�ɁA���_�ŐÎ~���Ă���דd���q���l����B���鎞������x���̐��̌����Ɉ��ň�l�ȓd����������Ƃ���A�דd���q�͔��aR�̋����ɂƂǂ܂炸��x����ʼn����^�����n�߂����A�������ɂ܂œ��B���邱�Ƃ͂Ȃ������B�ȉ��̖�ɓ�����B
�̏ꍇ�ɁA���_�ŐÎ~���Ă���דd���q���l����B���鎞������x���̐��̌����Ɉ��ň�l�ȓd����������Ƃ���A�דd���q�͔��aR�̋����ɂƂǂ܂炸��x����ʼn����^�����n�߂����A�������ɂ܂œ��B���邱�Ƃ͂Ȃ������B�ȉ��̖�ɓ�����B
(f) �דd���q�̈ʒu�G�l���M�[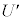 �́A���d�ׂ̕��z�����Ód�C�͂ɂ����̂ƈ�l�ȓd�ꂩ���Ód�C�͂ɂ����̘̂a�ŗ^������B���_����Ƃ���Ƃ��Ax����ɂ�����
�́A���d�ׂ̕��z�����Ód�C�͂ɂ����̂ƈ�l�ȓd�ꂩ���Ód�C�͂ɂ����̘̂a�ŗ^������B���_����Ƃ���Ƃ��Ax����ɂ�����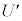 �̊T�`�Ƃ��čł��K���Ȃ��̂�}4�̑I�����@�`�I����I�сA�ԍ��œ�����B�������A���ꂼ��̃O���t�ɕ`����Ă���x�͈̔͊O�ł́A
�̊T�`�Ƃ��čł��K���Ȃ��̂�}4�̑I�����@�`�I����I�сA�ԍ��œ�����B�������A���ꂼ��̃O���t�ɕ`����Ă���x�͈̔͊O�ł́A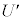 �͒P���ɑ������邢�͌�������������̂Ƃ���B
�͒P���ɑ������邢�͌�������������̂Ƃ���B
(g) �דd���q�����aR�̋����ɂƂǂ܂炸�ɉ^������悤�ȓd��̋����̉����ƂȂ�l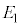 ���Ae�CR�Cm�Ck�̂����K�v�Ȃ��̂�p���ĕ\���B
���Ae�CR�Cm�Ck�̂����K�v�Ȃ��̂�p���ĕ\���B
(h) �דd���q���������ɂ܂œ��B���Ȃ��悤�ȓd��̋����̏���ƂȂ�l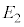 ���Ae�CR�Cm�Ck�̂����K�v�Ȃ��̂�p���ĕ\���B
���Ae�CR�Cm�Ck�̂����K�v�Ȃ��̂�p���ĕ\���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���Ȃ萔�w�I������v��������ł��B�����ɂ��[�����ӂ��K�v�ł��B
[A](a) ���aR�̋��̑̐ς�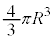 �C���̒��ɐ��d��e����l�ɕ��z���Ă���̂ŁA���_�𒆐S�Ƃ��锼�ar (
�C���̒��ɐ��d��e����l�ɕ��z���Ă���̂ŁA���_�𒆐S�Ƃ��锼�ar (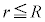 )�ŋ��̑̐�
)�ŋ��̑̐�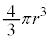 �̋��̓����̓d�ׂ́A
�̋��̓����̓d�ׂ́A ���̓d�ׂ����_�ɏW�����Ă���Ƃ��āA��蕶�̃q���g���A�דd���q�����N�[�������̑傫��F�́A 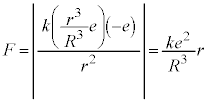 �@����@
�@����@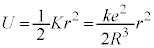 �@����A
�@����A����āA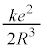 ......[�C]���邢�́A�N�[�����͂ɋt�炤�O��
......[�C]���邢�́A�N�[�����͂ɋt�炤�O��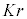 (���S����O����)���דd���q��
(���S����O����)���דd���q��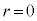 (���_����ł�)����ʒur�܂Ŏ����Ă����d�����l���āA
(���_����ł�)����ʒur�܂Ŏ����Ă����d�����l���āA 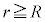 �̏ꍇ�́A���_�ɓd��e���W�����Ă���ƍl���āA�דd���q�����N�[�������̑傫��F�́A
�̏ꍇ�́A���_�ɓd��e���W�����Ă���ƍl���āA�דd���q�����N�[�������̑傫��F�́A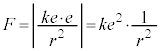 �C����āA
�C����āA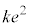 ......[�E]
......[�E]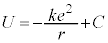 �@����B
�@����B����āA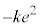 ......[�G]���邢�́A�N�[�����͂ɋt�炤�O��
......[�G]���邢�́A�N�[�����͂ɋt�炤�O��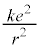 (���S����O����)�̂����d���ƍl����ƁA
(���S����O����)�̂����d���ƍl����ƁA 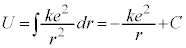 (C�F�ϕ��萔)
(C�F�ϕ��萔)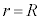 �ɂ����āA�A�ƇB����v����Ƃ��āA
�ɂ����āA�A�ƇB����v����Ƃ��āA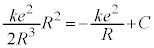 �@��
�@�� 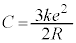 ......[�I]
......[�I]������B�́A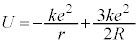 (
(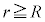 ) ����C
) ����C
�����ŁA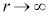 �Ƃ���ƁA
�Ƃ���ƁA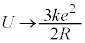
���_�ŐÎ~���Ă���̂ʼn^���G�l���M�[��0�C�דd���q�����ɂ܂ň��������d����W�̂Ƃ��A�G�l���M�[�̌������A�������ł̉^���G�l���M�[�́A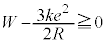
����āA�ŏ��̎d���́A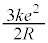 ......[�J]
......[�J]
 (b) �E�}��A
(b) �E�}��A �ɂ���דd���q
�ɂ���דd���q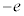 �����_�ɏW�����Ă��鐳�d��
�����_�ɏW�����Ă��鐳�d��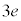 �����͂�x����������(�A)�Ɠ��l�ɁA
�����͂�x����������(�A)�Ɠ��l�ɁA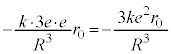 �@����D
�@����DA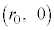 ��B
��B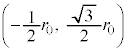 �Ƃ̋�����BC�ɓ������A3�̉דd���q�����O�p�`�̒��_�Ɉʒu���Ă��邱�Ƃ���A
�Ƃ̋�����BC�ɓ������A3�̉דd���q�����O�p�`�̒��_�Ɉʒu���Ă��邱�Ƃ���A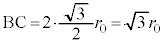
�E�}A�_�ɂ���דd���q��B�_�ɂ���דd���q �����͂͐˗͂ŁA�E�}�̃x�N�g��
�����͂͐˗͂ŁA�E�}�̃x�N�g�� �̕���(x����������
�̕���(x����������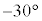 ���Ȃ�����)�ł��̑傫���́A
���Ȃ�����)�ł��̑傫���́A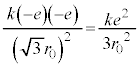 A�_�ɂ���דd���q��C�_�ɂ���דd���q
A�_�ɂ���דd���q��C�_�ɂ���דd���q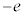 �����͂́A�E�}�̃x�N�g��
�����͂́A�E�}�̃x�N�g��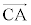 �̕���(x����������
�̕���(x����������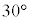 ���Ȃ�����)�ő傫����
���Ȃ�����)�ő傫����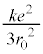 �C����2�̗͂̍��͂�x���������ŁA
�C����2�̗͂̍��͂�x���������ŁA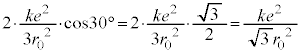 �@����E
�@����E
�D�ƇE�̗͂̂荇�����A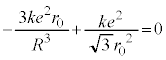 �@��
�@�� 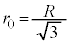 ......[��]
......[��]
(d) �����~�^���̎�����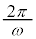 �ł��B�d���͎��v���ŕ��ł��B�d��I�́A�d��
�ł��B�d���͎��v���ŕ��ł��B�d��I�́A�d��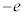 ������
������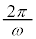 ��������1�����邱�ƂƁA���ς��l����Ƃ����q���g����Aω���g���ē����邱�Ƃɒ��ӂ��āA
��������1�����邱�ƂƁA���ς��l����Ƃ����q���g����Aω���g���ē����邱�Ƃɒ��ӂ��āA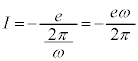 ......[��]
......[��]
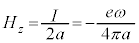 ......[��]
......[��]
[C]�@x���̐��̌����Ɉ�l���d���̋�����E�Ƃ��āA���̓d�ꂪ�ʒux�ɍ���d����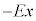 �C�דd���q
�C�דd���q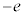 �̈ʒu�G�l���M�[�́A
�̈ʒu�G�l���M�[�́A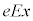 �ł��B
�ł��B
(f) [A]�ōl�����ʒu�G�l���M�[�͌��_����ɂ��Ă��āA�����ł����_����ɂ��čl����̂ŁA[A]�̌��ʂ��g���čl���܂��B���_�ɐÎ~���Ă���דd���q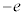 ��x���������Ɍ������d�ꂩ��x���������ɗ͂��ē����o���܂��B�����o������́A
��x���������Ɍ������d�ꂩ��x���������ɗ͂��ē����o���܂��B�����o������́A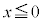 �ɗ���̂�[A]��
�ɗ���̂�[A]��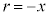 �ƍl���A
�ƍl���A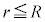 �܂�
�܂�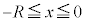 �̂Ƃ��A�דd���q�̈ʒu�G�l���M�[�́A�A��
�̂Ƃ��A�דd���q�̈ʒu�G�l���M�[�́A�A��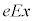 �����킹�āA
�����킹�āA 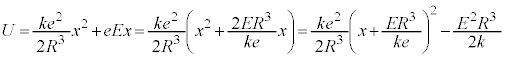 �@����F
�@����F���̃O���t�́A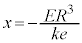 �����Ƃ��鉺�ɓʂȕ������ł�(2�������Q��)�B
�����Ƃ��鉺�ɓʂȕ������ł�(2�������Q��)�B
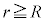 �܂�
�܂�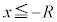 �̂Ƃ��A�דd���q�̈ʒu�G�l���M�[�́A�C��
�̂Ƃ��A�דd���q�̈ʒu�G�l���M�[�́A�C��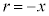 �Ƃ������̂�
�Ƃ������̂�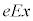 �����킹�āA
�����킹�āA 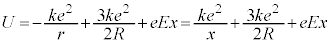 �@����G
�@����G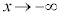 �̂Ƃ�
�̂Ƃ�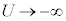 �ł��B
�ł��B
�܂��A���aR�̋����ɂƂǂ܂�Ȃ��������Ƃ���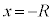 �ɂ�����ʒu�G�l���M�[�͌��_�ɂ�����ʒu�G�l���M�[
�ɂ�����ʒu�G�l���M�[�͌��_�ɂ�����ʒu�G�l���M�[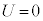 �����������Ȃ�܂��B
�����������Ȃ�܂��B
�ȏ�̂悤�ɂȂ��Ă���O���t�́A�G ......[��]
(g) (f)�ł��������悤�ɁA�דd���q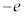 �����aR�̋����ɂƂǂ܂�Ȃ��������Ƃ���A�F��
�����aR�̋����ɂƂǂ܂�Ȃ��������Ƃ���A�F��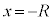 �̂Ƃ��A
�̂Ƃ��A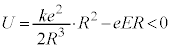 �C
�C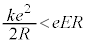
�� 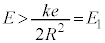 �@
�@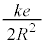 ......[��]
......[��] ���D(f)�ŃO���t�Ƃ��ćG��I��ł���̂ŁA�F�̃O���t(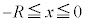 )���A
)���A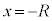 �̂Ƃ��̂݊m�F����Ώ\���ł��B�A���A
�̂Ƃ��̂݊m�F����Ώ\���ł��B�A���A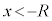 �̏ꍇ���l���āA�G����������ƁA
�̏ꍇ���l���āA�G����������ƁA ���AU��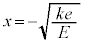 �ŋɑ�ɂȂ�܂����A�ɑ��^����x��
�ŋɑ�ɂȂ�܂����A�ɑ��^����x��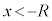 �����K�v������̂ŁA
�����K�v������̂ŁA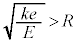 �C�܂�
�C�܂�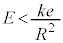 �C(g)�̌��ʂƍ��킹��
�C(g)�̌��ʂƍ��킹��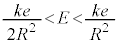 �ł���K�v������܂��B�܂��A�F�̎��̈ʒu�́A
�ł���K�v������܂��B�܂��A�F�̎��̈ʒu�́A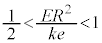 ���A
���A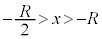 (���
(���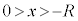 �̍����)�ɂ���܂��B
�̍����)�ɂ���܂��B
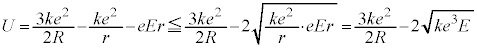 �@����H
�@����H�����́A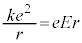 �C�܂�
�C�܂�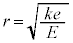 (
(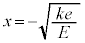 )�̂Ƃ��B
)�̂Ƃ��B
�����ŁA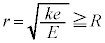 ���A
���A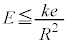 �@����I
�@����I
����U�̍ő�l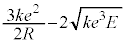 ��0�ȏ�ł���A�דd���q�͖������ɓ��B���܂���B����āA
��0�ȏ�ł���A�דd���q�͖������ɓ��B���܂���B����āA 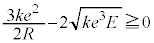 �C
�C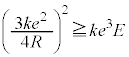
�� 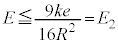 (
(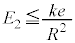 ���I�����Ă��܂�)�@
���I�����Ă��܂�)�@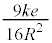 ......[��]
......[��] ���D(g)�̒���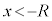 �ɂ�����
�ɂ�����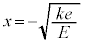 ��U���ɑ�Ə����܂������A�G��
��U���ɑ�Ə����܂������A�G��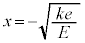 �Ƃ��Ă��A�H�̍ő�l�������܂��B���ǁA(g)�̒��ɁA�������ɍs���Ȃ��Ƃ���������������ƁA�d��E�́A
�Ƃ��Ă��A�H�̍ő�l�������܂��B���ǁA(g)�̒��ɁA�������ɍs���Ȃ��Ƃ���������������ƁA�d��E�́A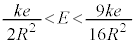 �����K�v������܂��B
�����K�v������܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 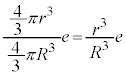
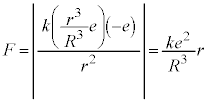 �@����@
�@����@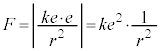 �C����āA
�C����āA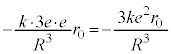 �@����D
�@����D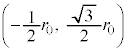 �Ƃ̋�����BC�ɓ������A3�̉דd���q�����O�p�`�̒��_�Ɉʒu���Ă��邱�Ƃ���A
�Ƃ̋�����BC�ɓ������A3�̉דd���q�����O�p�`�̒��_�Ɉʒu���Ă��邱�Ƃ���A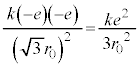
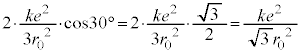 �@����E
�@����E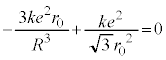 �@��
�@�� 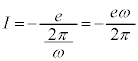 ......[��]
......[��]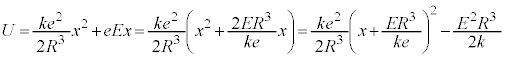 �@����F
�@����F