東京工業大学2023年前期物理入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
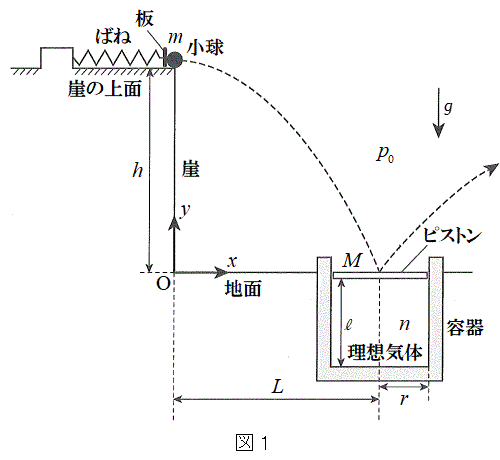 [1] 図1のように、地面からの高さがhの鉛直な崖の上面から大きさの無視できる質量mの小球をばねを使って水平方向に射出し、円筒形の容器の中を滑らかに動くことのできるピストンの上に落下させる。ばねの左端は固定されており、右端には小球を押し出すための板が取り付けられていて、ばねが自然長のとき板は崖のふちに一致している。ばねのばね定数はkである。ここで、崖の上面は水平であり、小球との静止摩擦係数をμ,動摩擦係数を
[1] 図1のように、地面からの高さがhの鉛直な崖の上面から大きさの無視できる質量mの小球をばねを使って水平方向に射出し、円筒形の容器の中を滑らかに動くことのできるピストンの上に落下させる。ばねの左端は固定されており、右端には小球を押し出すための板が取り付けられていて、ばねが自然長のとき板は崖のふちに一致している。ばねのばね定数はkである。ここで、崖の上面は水平であり、小球との静止摩擦係数をμ,動摩擦係数を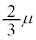 とする。容器は水平な地面に埋め込まれており、その中心軸は鉛直線に平行で崖からの距離がLの位置にある。ピストンは半径rの円板で、ピストンの質量はM (
とする。容器は水平な地面に埋め込まれており、その中心軸は鉛直線に平行で崖からの距離がLの位置にある。ピストンは半径rの円板で、ピストンの質量はM (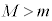 )であり、容器の内部は単原子分子からなるnモルの理想気体で満たされている。また、ピストンは鉛直方向にのみ動き、傾くことはないものとする。最初、ピストンは静止しており、ピストンの上面は地面と同じ高さにあり、下面は容器の底から
)であり、容器の内部は単原子分子からなるnモルの理想気体で満たされている。また、ピストンは鉛直方向にのみ動き、傾くことはないものとする。最初、ピストンは静止しており、ピストンの上面は地面と同じ高さにあり、下面は容器の底から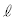 だけ離れている。
だけ離れている。
以下では重力加速度の大きさを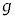 ,気体定数をR,大気圧を
,気体定数をR,大気圧を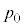 とし、ばねと板の質量、および空気抵抗は無視できるものとする。また、崖の上面と板の摩擦は無視し、小球とピストンの衝突は弾性衝突であるとする。ただし、小球が容器に衝突することはないとする。水平右向きにx軸をとり、崖のふちを
とし、ばねと板の質量、および空気抵抗は無視できるものとする。また、崖の上面と板の摩擦は無視し、小球とピストンの衝突は弾性衝突であるとする。ただし、小球が容器に衝突することはないとする。水平右向きにx軸をとり、崖のふちを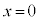 とする。また、鉛直上向きにy軸をとり、地面の高さを
とする。また、鉛直上向きにy軸をとり、地面の高さを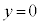 とする。さらに、小球、ばね、および容器の中心軸はxy平面内にあり、すべての運動はxy平面内に限られているとする。
とする。さらに、小球、ばね、および容器の中心軸はxy平面内にあり、すべての運動はxy平面内に限られているとする。
[A] 小球を板に押しあてて、ばねを縮めながら、小球を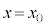 (
(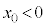 )まで移動させ、静止した状態で小球を放す実験を様々な
)まで移動させ、静止した状態で小球を放す実験を様々な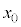 について行った。以下の問いに答えよ。
について行った。以下の問いに答えよ。
(a) 小球を放した後、小球が動き出すためには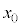 がある値より小さくなければならない。この値を
がある値より小さくなければならない。この値を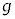 ,m,k,μのうち必要なものを用いて表せ。解答欄には答えのみ書くこと。
,m,k,μのうち必要なものを用いて表せ。解答欄には答えのみ書くこと。
(b) 問(a)の条件が満たされるとき、動き出した小球の加速度が0となるxの位置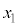 (
(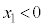 )を
)を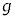 ,m,k,μ,
,m,k,μ,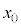 のうち必要なものを用いて表せ。
のうち必要なものを用いて表せ。
(c) 問(a)の条件が満たされているとき、動き出した小球が崖から飛び出すためには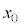 がある値より小さくなければならない。この値を
がある値より小さくなければならない。この値を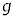 ,m,k,μのうち必要なものを用いて表せ。
,m,k,μのうち必要なものを用いて表せ。
(d) 問(a)と問(c)の条件が満たされており、小球がピストン上面の中心に落下した場合を考える。小球が崖から水平右向きに飛び出したときの速さ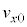 を
を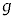 ,m,h,M,Lのうち必要なものを用いて表せ。
,m,h,M,Lのうち必要なものを用いて表せ。
[B] ピストンと容器は断熱材でできており、その中に理想気体が閉じ込められている。崖から飛び出した小球は、ピストン上面の中心に落下した後、ピストンと再び衝突することなく右方へと飛んで行き、ピストンは振動を始めた。ただし、ピストンと容器の間の摩擦は無視できるものとし、ピストンは容器から外れることはないとする。理想気体の状態変化は断熱変化とみなすことができ、理想気体の状態は十分にゆっくりと変化し、理想気体の圧力や温度はいつでも一様とみなせるとする。以下の問いに答えよ。
(e) ピストンの運動を考える前に、理想気体の断熱変化の性質を考察する。以下の空欄(ア)〜(エ)にあてはまる数式をV,p,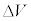 ,
,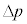 ,n,Rのうち必要なものを用いて表せ。解答欄には答のみ書くこと。
,n,Rのうち必要なものを用いて表せ。解答欄には答のみ書くこと。 初期状態の体積、圧力、温度がそれぞれV,p,Tにある理想気体に外力を加えることで、体積が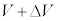 ,圧力が
,圧力が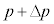 ,温度が
,温度が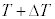 の状態へと微小変化した場合を考える。つまり、
の状態へと微小変化した場合を考える。つまり、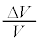 ,
,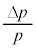 ,
,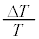 の絶対値は1より十分に小さい量である。これらの積を無視する近似をすると、理想気体の状態方程式から
の絶対値は1より十分に小さい量である。これらの積を無視する近似をすると、理想気体の状態方程式から  (1)
(1)の関係が成り立つ。
一方、理想気体の内部エネルギーの変化は である。また、微小変化の間の圧力の変化は小さいことから、理想気体がされた仕事は
である。また、微小変化の間の圧力の変化は小さいことから、理想気体がされた仕事は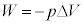 と近似できる。よって、
と近似できる。よって、 となり、
となり、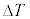 が
が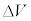 に近似的に比例する。この比例関係と式(1)より
に近似的に比例する。この比例関係と式(1)より  (2)
(2)となり、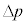 は
は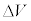 に近似的に比例することがわかる。
に近似的に比例することがわかる。
(f) 小球が衝突する前の理想気体の圧力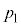 を
を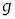 ,M,r,
,M,r,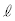 ,n,R,
,n,R,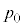 のうち必要なものを用いて表せ。
のうち必要なものを用いて表せ。
(g) 小球とピストンの衝突直後のピストンの速度のy成分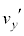 を
を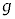 ,m,M,L,h,r,
,m,M,L,h,r,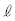 ,n,Rのうち必要なものを用いて表せ。ただし、衝突中にピストンが大気および理想気体から受ける力積は無視できるものとする。
,n,Rのうち必要なものを用いて表せ。ただし、衝突中にピストンが大気および理想気体から受ける力積は無視できるものとする。
(h) 小球が衝突した後,ピストンが振動しているときの運動を考える。ピストンが初期状態と比べてyだけ鉛直上向きに動いたとき、ピストンにはたらく力の合力のy成分を とする。
とする。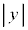 が微小量であるとして、問(e)の式(2)を使い、
が微小量であるとして、問(e)の式(2)を使い、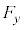 を
を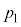 ,r,
,r,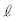 ,yのうち必要なものを用いて表せ。
,yのうち必要なものを用いて表せ。
(i) 問(h)で得られた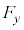 は、比例係数を
は、比例係数を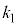 として、変位yに対する復元力
として、変位yに対する復元力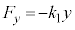 と考えられる。このとき、ピストンの振動を単振動とみなして振幅
と考えられる。このとき、ピストンの振動を単振動とみなして振幅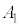 をM,
をM,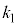 ,r,yおよび問(g)の
,r,yおよび問(g)の のうち必要なものを用いて表せ。
のうち必要なものを用いて表せ。
[解答へ]
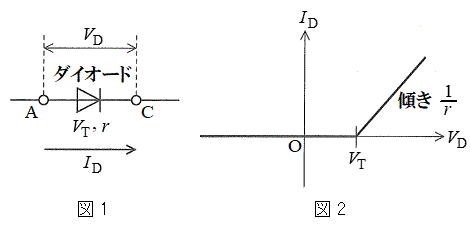 [2] ダイオードは、p型半導体とn型半導体を接合した素子で、整流作用を示す。図1のように、ダイオードの端子Cの電位を基準とする端子Aの電位を電位差
[2] ダイオードは、p型半導体とn型半導体を接合した素子で、整流作用を示す。図1のように、ダイオードの端子Cの電位を基準とする端子Aの電位を電位差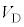 とし、右向きに流れる電流を
とし、右向きに流れる電流を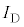 とする。本問題におけるすべてのダイオードは、図2のグラフの電流電圧特性を示す。図2の特性は、電流が流れ始める電圧
とする。本問題におけるすべてのダイオードは、図2のグラフの電流電圧特性を示す。図2の特性は、電流が流れ始める電圧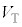 および内部抵抗rで説明することができる。
および内部抵抗rで説明することができる。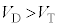 における電流電圧特性の傾きは
における電流電圧特性の傾きは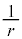 であり、
であり、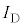 と
と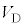 の関係は次の式で与えられるものとする。
の関係は次の式で与えられるものとする。
すなわち、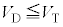 である場合にはダイオードを絶縁体とみなすことができ、
である場合にはダイオードを絶縁体とみなすことができ、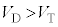 である場合にはpn接合に一定の電圧降下
である場合にはpn接合に一定の電圧降下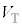 が発生し、残りの電圧
が発生し、残りの電圧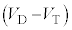 がダイオードの内部抵抗rに加わることで、
がダイオードの内部抵抗rに加わることで、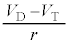 の電流が流れると考えることができる。
の電流が流れると考えることができる。
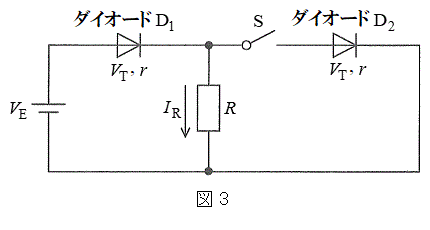 [A] 図3のように、起電力
[A] 図3のように、起電力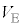 の直流電源、ダイオード
の直流電源、ダイオード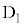 ,
,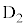 ,電気抵抗Rの抵抗、スイッチSを接続した。抵抗を矢印の向きに流れる電流
,電気抵抗Rの抵抗、スイッチSを接続した。抵抗を矢印の向きに流れる電流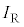 について、以下の問いに答えよ。ただし、直流電源の内部抵抗は無視できるものとする。
について、以下の問いに答えよ。ただし、直流電源の内部抵抗は無視できるものとする。
(a) スイッチSが開いている場合、抵抗に矢印の向きに0ではない電流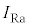 が流れた。このことから、
が流れた。このことから、 はある値
はある値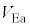 よりも大きかったことがわかる。
よりも大きかったことがわかる。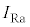 と
と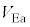 を
を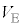 ,
,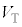 ,r,Rのうち必要なものを用いて表せ。
,r,Rのうち必要なものを用いて表せ。
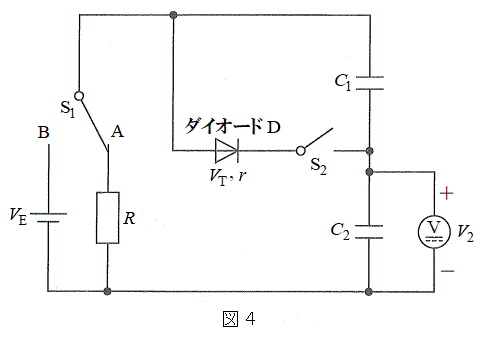 [B] 図4のように、起電力
[B] 図4のように、起電力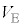 の直流電源、ダイオードD,電気容量
の直流電源、ダイオードD,電気容量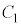 ,
,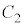 のコンデンサー、電気抵抗Rの抵抗、電圧計、スイッチ
のコンデンサー、電気抵抗Rの抵抗、電圧計、スイッチ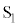 ,
,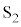 を接続した。電圧計は、マイナス端子(−)の電位に対するプラス端子(+)の電位の差
を接続した。電圧計は、マイナス端子(−)の電位に対するプラス端子(+)の電位の差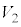 を測定できるものとする。はじめに、スイッチ
を測定できるものとする。はじめに、スイッチ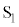 はA側にあり、スイッチ
はA側にあり、スイッチ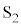 は開いており、どのコンデンサーも電荷を蓄えていなかったものとする。以下の問いに答えよ。ただし、直流電源の内部抵抗は無視でき、電圧計の内部抵抗は無限大であるとする。
は開いており、どのコンデンサーも電荷を蓄えていなかったものとする。以下の問いに答えよ。ただし、直流電源の内部抵抗は無視でき、電圧計の内部抵抗は無限大であるとする。
(c) スイッチ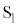 をB側に入れたところ、コンデンサーに電荷が蓄えられ、電圧計はある一定値
をB側に入れたところ、コンデンサーに電荷が蓄えられ、電圧計はある一定値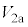 を示した。その後、スイッチ
を示した。その後、スイッチ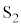 を閉じて十分に時間が経過すると、電圧計は
を閉じて十分に時間が経過すると、電圧計は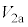 とは異なる一定の値
とは異なる一定の値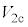 を示した。後者の電圧変化が起きたことから、
を示した。後者の電圧変化が起きたことから、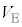 はある値
はある値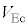 よりも大きかったことがわかる。
よりも大きかったことがわかる。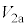 ,
,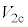 ,
,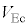 を
を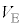 ,
, ,
,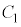 ,
,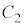 ,rのうち必要なものを用いて表せ。
,rのうち必要なものを用いて表せ。
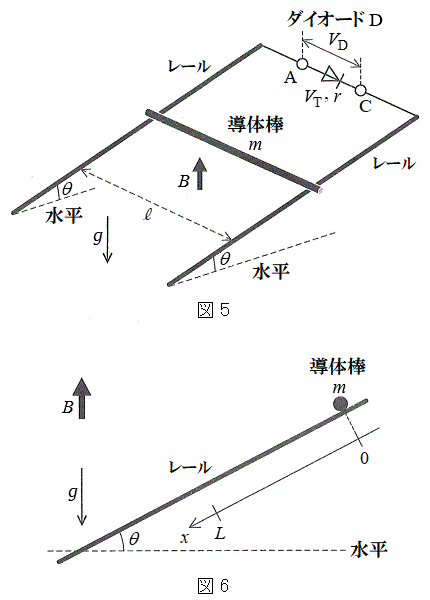 [C] 図5のように、鉛直上向きに磁束密度B (
[C] 図5のように、鉛直上向きに磁束密度B (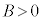 )の一様で時間的に変化しない磁場がかかっており、水平面から角度θ (
)の一様で時間的に変化しない磁場がかかっており、水平面から角度θ (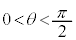 )だけ傾いた2本の導体のレールが間隔
)だけ傾いた2本の導体のレールが間隔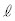 で平行に置かれている。質量がmで太さを無視できる導体棒が2本のレールの上に置かれて接している。導体棒は、レールと直交した状態を維持しながら摩擦や空気抵抗の影響を受けることなく移動できる。また、2本のレールの間にはダイオードDが接続されている。先に定義したように端子Cに対する端子Aの電位差を
で平行に置かれている。質量がmで太さを無視できる導体棒が2本のレールの上に置かれて接している。導体棒は、レールと直交した状態を維持しながら摩擦や空気抵抗の影響を受けることなく移動できる。また、2本のレールの間にはダイオードDが接続されている。先に定義したように端子Cに対する端子Aの電位差を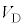 とする。重力加速度の大きさを
とする。重力加速度の大きさを とする。図6は、導体棒が点に見える方向から見た図を示しており、レールに沿って下る向きにx軸をとる。
とする。図6は、導体棒が点に見える方向から見た図を示しており、レールに沿って下る向きにx軸をとる。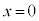 の位置に導体棒を置き、時刻
の位置に導体棒を置き、時刻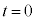 で静かに導体棒を放したところ、導体棒はレールの上を動き始めた。その後、ある時刻
で静かに導体棒を放したところ、導体棒はレールの上を動き始めた。その後、ある時刻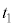 に達するまでは、ダイオードDには電流は流れず、時刻
に達するまでは、ダイオードDには電流は流れず、時刻 を超えるとダイオードDに電流が流れるようになった。十分に時間が経過すると導体棒の速度は一定になった。さらに時間が経過すると、導体棒は
を超えるとダイオードDに電流が流れるようになった。十分に時間が経過すると導体棒の速度は一定になった。さらに時間が経過すると、導体棒は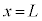 に達した。以下の問いに答えよ。ただし、回路に流れる電流により発生する磁場、レールと導体棒の電気抵抗、回路の電気容量は無視できるものとする。また、レールは十分に長く、導体棒がレールの端に達することはないものとする。
に達した。以下の問いに答えよ。ただし、回路に流れる電流により発生する磁場、レールと導体棒の電気抵抗、回路の電気容量は無視できるものとする。また、レールは十分に長く、導体棒がレールの端に達することはないものとする。
(e) ダイオードDに電流が流れていない時刻t (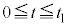 )における電位差
)における電位差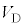 を、t の関数
を、t の関数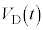 としてt,m,
としてt,m,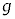 ,r,B,
,r,B,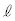 ,θ,
,θ,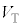 のうち必要なものを用いて表せ。ただし、このとき導体棒およびレールには電流は流れていないとみなしてよい。
のうち必要なものを用いて表せ。ただし、このとき導体棒およびレールには電流は流れていないとみなしてよい。
(f) 時刻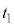 を求めよ。ただし、m,
を求めよ。ただし、m,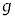 ,r,B,
,r,B,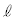 ,θ,
,θ,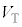 のうち必要なものを用いて表せ。
のうち必要なものを用いて表せ。
(g) 導体棒が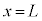 に達したときの
に達したときの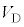 の値
の値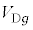 を求めよ。ただし、m,
を求めよ。ただし、m,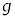 ,r,B,
,r,B,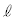 ,θ,
,θ,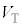 のうち必要なものを用いて表せ。
のうち必要なものを用いて表せ。
(h) 導体棒が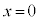 から
から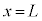 まで移動した間に、ダイオードDで消費された電力量Wを求めよ。ただし、問(g)における
まで移動した間に、ダイオードDで消費された電力量Wを求めよ。ただし、問(g)における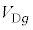 と、m,
と、m,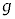 ,B,
,B,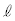 ,θ,Lのうち必要なものを用いて表せ。
,θ,Lのうち必要なものを用いて表せ。 [解答へ]
[3][A] X線を用いて、結晶の格子による回折実験を行う。結晶中の原子は点とみなすことができ、X線が点状の一つの原子によって散乱される場合、エネルギーを失うことなくあらゆる方向に散乱されるものとする。一つの原子によってX線が散乱される確率は非常に小さいため、結晶の表面から深いところまで散乱されずに侵入するX線の割合は十分大きく、すべの原子から散乱されたX線が同位相で強め合う(経路差がX線の波長の整数倍となる)場合に、X線回折が起こる。X線は結晶に入射する際に結晶表面で屈折することはなく、また、一回散乱されたX線が再び別の原子により散乱される効果は無視できるものとする。図1および図2で黒丸は原子の位置を表しており、結晶の原子配列は縦、横、奥行き方向に等間隔aで並んだものとする。X線の波長をλとし、紙面内において、表面の原子配列に対してθの角度から入射した平面波のX線が、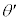 の角度で回折する条件について考える。ただし、
の角度で回折する条件について考える。ただし、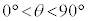 ,
,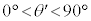 の範囲に限る。以下の問いに答えよ。
の範囲に限る。以下の問いに答えよ。
(c) 以下はX線回折が起こる条件の説明文である。空欄(ア),(イ),(ウ)にあてはまる数式を、問(a)のN,問(b)のM,a,λを用いて答えよ。ただし、解が存在するためのN,Mの条件は答えなくてよい。必要であれば、任意の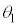 ,
,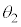 に対して
に対して の関係が成り立つことを用いてよい。
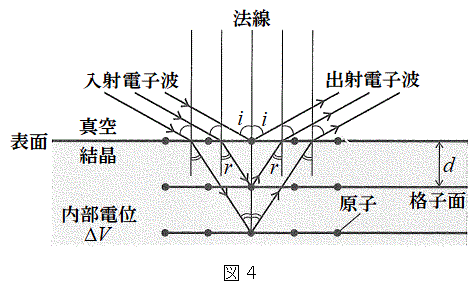 [B] 電子は粒子であるとともに物質波(電子波)としても振る舞う。よって電子波の波長が原子間隔程度に短ければ、X線の場合と同様に結晶の格子による回折が起こる。図4のように、結晶は真空中に置かれ、真空中の電位は0で一様であり、結晶内部の電位は
[B] 電子は粒子であるとともに物質波(電子波)としても振る舞う。よって電子波の波長が原子間隔程度に短ければ、X線の場合と同様に結晶の格子による回折が起こる。図4のように、結晶は真空中に置かれ、真空中の電位は0で一様であり、結晶内部の電位は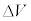 (
(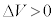 )で一様であるとする。ただし、電位の変化は結晶表面近傍の厚さが無視できる範囲内でのみ起こっているとする。電子は電荷を帯びており、電子が真空中から結晶中に入るときに、この電位差
)で一様であるとする。ただし、電位の変化は結晶表面近傍の厚さが無視できる範囲内でのみ起こっているとする。電子は電荷を帯びており、電子が真空中から結晶中に入るときに、この電位差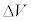 によって速度が変化し、電子波は結晶表面で屈折する。
によって速度が変化し、電子波は結晶表面で屈折する。静止した電子を、遠方で電位差V (加速電圧、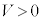 )で加速させることで平面波の電子線(同じ向きに進む電子の流れ)をつくり、電子の運動エネルギーを失うことなく、結晶表面に電子線を到達させた。紙面内で、結晶表面の法線に対して入射角i (
)で加速させることで平面波の電子線(同じ向きに進む電子の流れ)をつくり、電子の運動エネルギーを失うことなく、結晶表面に電子線を到達させた。紙面内で、結晶表面の法線に対して入射角i (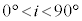 )で電子線を入射し、屈折角rで屈折する場合を考える。表面に平行な格子面で鏡面反射した結晶中の電子波は、法線に対して角度iで結晶表面から出射する。この際に、表面に平行なすべての格子面で鏡面反射した電子線が同位相で強め合う場合に、電子線回折が起こる(この実験では表面での反射における位相の反転は起こらない)。結晶の表面に平行な格子面の間隔をd,プランク定数をh,電子の質量をm,電子の電荷を
)で電子線を入射し、屈折角rで屈折する場合を考える。表面に平行な格子面で鏡面反射した結晶中の電子波は、法線に対して角度iで結晶表面から出射する。この際に、表面に平行なすべての格子面で鏡面反射した電子線が同位相で強め合う場合に、電子線回折が起こる(この実験では表面での反射における位相の反転は起こらない)。結晶の表面に平行な格子面の間隔をd,プランク定数をh,電子の質量をm,電子の電荷を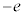 (
(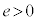 )として以下の問いに答えよ。
)として以下の問いに答えよ。
(d) 電子の粒子としての速さについて、真空中における値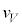 と、結晶中における値
と、結晶中における値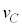 を、h,m,e,V,
を、h,m,e,V,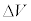 の中から必要なものを用いて表せ。
の中から必要なものを用いて表せ。
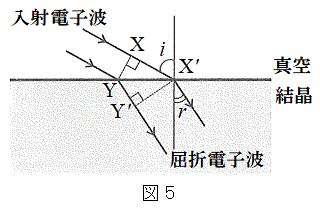 (f) 図5のように入射電子波がYに到達したときの波面XYが、屈折電子波の波面
(f) 図5のように入射電子波がYに到達したときの波面XYが、屈折電子波の波面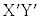 へと進む際に、真空中での経路
へと進む際に、真空中での経路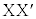 における位相変化と結晶中の経路
における位相変化と結晶中の経路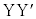 における位相変化は等しい。このことを利用して、電子線が真空から結晶に入射するときの屈折率
における位相変化は等しい。このことを利用して、電子線が真空から結晶に入射するときの屈折率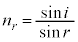 を、h,m,e,V,
を、h,m,e,V,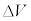 の中から必要なものを用いて表せ。ただし、電子の粒子として進む速さと電子波の波面が進む速さは異なり、
の中から必要なものを用いて表せ。ただし、電子の粒子として進む速さと電子波の波面が進む速さは異なり、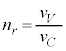 とはならない。
とはならない。
(g) 真空中と結晶中で、電子の粒子としての運動量がどう変化したかを考える。結晶中で、電子の粒子としての運動を観測したところ、問(f)の屈折電子波と同じ方向に運動していることが分かった。結晶中の運動量の、表面に平行な成分の大きさ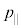 と、表面に垂直な成分の大きさ
と、表面に垂直な成分の大きさ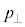 を、
を、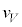 とi を必ず含め、h,m,e,
とi を必ず含め、h,m,e,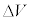 の中から必要なものを用いて表せ。
の中から必要なものを用いて表せ。
(h) いろいろな加速電圧Vでつくった電子線を用いて、ある入射角i と反射角i で電子線回折を起こすかどうかを調べたところ、複数のVにおいて回折条件を満たすことが分かった。回折条件を満たすVを、h,m,e,d,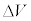 ,i,整数nの中から必要なものを用いて表せ。ただし、解が存在するためのnの条件は答えなくてよい。
,i,整数nの中から必要なものを用いて表せ。ただし、解が存在するためのnの条件は答えなくてよい。 [解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東工大物理TOP 物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 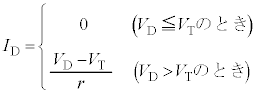
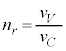 とはならない。
とはならない。