���H�啨��'23�N�O��[3]
[A]�@X����p���āA�����̊i�q�ɂ���������s���B�������̌��q�͓_�Ƃ݂Ȃ����Ƃ��ł��AX�����_��̈�̌��q�ɂ���ĎU�������ꍇ�A�G�l���M�[���������ƂȂ�����������ɎU���������̂Ƃ���B��̌��q�ɂ����X�����U�������m���͔��ɏ��������߁A�����̕\�ʂ���[���Ƃ���܂ŎU�����ꂸ�ɐN������X���̊����͏\���傫���A���ׂ̌��q����U�����ꂽX�������ʑ��ŋ��ߍ���(�o�H����X���̔g���̐����{�ƂȂ�)�ꍇ�ɁAX����܂��N����BX���͌����ɓ��˂���ۂɌ����\�ʂŋ��܂��邱�Ƃ͂Ȃ��A�܂��A���U�����ꂽX�����Ăѕʂ̌��q�ɂ��U���������ʂ͖����ł�����̂Ƃ���B�}1����ѐ}2�ō��ۂ͌��q�̈ʒu��\���Ă���A�����̌��q�z��͏c�A���A���s�������ɓ��Ԋua�ŕ����̂Ƃ���BX���̔g����λ�Ƃ��A���ʓ��ɂ����āA�\�ʂ̌��q�z��ɑ���θ�̊p�x������˂������ʔg��X�����A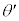 �̊p�x�ʼn�܂�������ɂ��čl����B�������A
�̊p�x�ʼn�܂�������ɂ��čl����B�������A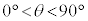 �C
�C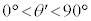 �͈̔͂Ɍ���B�ȉ��̖₢�ɓ�����B
�͈̔͂Ɍ���B�ȉ��̖₢�ɓ�����B
(c) �ȉ���X����܂��N��������̐������ł���B��(�A)�C(�C)�C(�E)�ɂ��Ă͂܂鐔�����A��(a)��N�C��(b)��M�Ca�Cλ��p���ē�����B�������A�������݂��邽�߂�N�CM�̏����͓����Ȃ��Ă悢�B�K�v�ł���A�C�ӂ�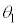 �C
�C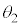 �ɑ���
�ɑ��� �̊W�����藧���Ƃ�p���Ă悢�B
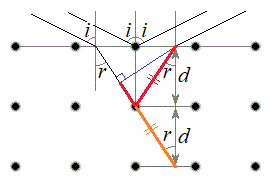
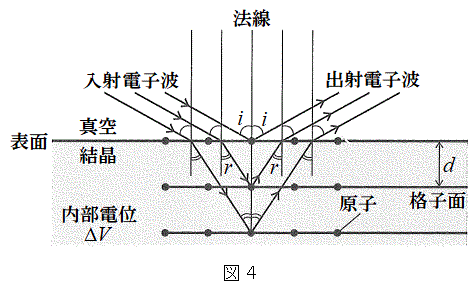 [B]�@�d�q�͗��q�ł���ƂƂ��ɕ����g(�d�q�g)�Ƃ��Ă��U�镑���B����ēd�q�g�̔g�������q�Ԋu���x�ɒZ����AX���̏ꍇ�Ɠ��l�Ɍ����̊i�q�ɂ���܂��N����B�}4�̂悤�ɁA�����͐^�ɒu����A�^�̓d�ʂ�0�ň�l�ł���A���������̓d�ʂ�
[B]�@�d�q�͗��q�ł���ƂƂ��ɕ����g(�d�q�g)�Ƃ��Ă��U�镑���B����ēd�q�g�̔g�������q�Ԋu���x�ɒZ����AX���̏ꍇ�Ɠ��l�Ɍ����̊i�q�ɂ���܂��N����B�}4�̂悤�ɁA�����͐^�ɒu����A�^�̓d�ʂ�0�ň�l�ł���A���������̓d�ʂ�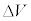 (
(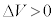 )�ň�l�ł���Ƃ���B�������A�d�ʂ̕ω��͌����\�ʋߖT�̌����������ł���͈͓��ł̂N�����Ă���Ƃ���B�d�q�͓d�ׂ�ттĂ���A�d�q���^���猋�����ɓ���Ƃ��ɁA���̓d�ʍ�
)�ň�l�ł���Ƃ���B�������A�d�ʂ̕ω��͌����\�ʋߖT�̌����������ł���͈͓��ł̂N�����Ă���Ƃ���B�d�q�͓d�ׂ�ттĂ���A�d�q���^���猋�����ɓ���Ƃ��ɁA���̓d�ʍ�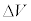 �ɂ���đ��x���ω����A�d�q�g�͌����\�ʂŋ��܂���B
�ɂ���đ��x���ω����A�d�q�g�͌����\�ʂŋ��܂���B�Î~�����d�q���A�����œd�ʍ�V (�����d���A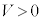 )�ʼn��������邱�Ƃŕ��ʔg�̓d�q��(���������ɐi�ޓd�q�̗���)������A�d�q�̉^���G�l���M�[���������ƂȂ��A�����\�ʂɓd�q���B�������B���ʓ��ŁA�����\�ʂ̖@���ɑ��ē��ˊpi (
)�ʼn��������邱�Ƃŕ��ʔg�̓d�q��(���������ɐi�ޓd�q�̗���)������A�d�q�̉^���G�l���M�[���������ƂȂ��A�����\�ʂɓd�q���B�������B���ʓ��ŁA�����\�ʂ̖@���ɑ��ē��ˊpi (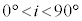 )�œd�q������˂��A���܊pr�ŋ��܂���ꍇ���l����B�\�ʂɕ��s�Ȋi�q�ʂŋ��ʔ��˂����������̓d�q�g�́A�@���ɑ��Ċp�xi�Ō����\�ʂ���o�˂���B���̍ۂɁA�\�ʂɕ��s�Ȃ��ׂĂ̊i�q�ʂŋ��ʔ��˂����d�q�������ʑ��ŋ��ߍ����ꍇ�ɁA�d�q����܂��N����(���̎����ł͕\�ʂł̔��˂ɂ�����ʑ��̔��]�͋N����Ȃ�)�B�����̕\�ʂɕ��s�Ȋi�q�ʂ̊Ԋu��d�C�v�����N�萔��h�C�d�q�̎��ʂ�m�C�d�q�̓d�ׂ�
)�œd�q������˂��A���܊pr�ŋ��܂���ꍇ���l����B�\�ʂɕ��s�Ȋi�q�ʂŋ��ʔ��˂����������̓d�q�g�́A�@���ɑ��Ċp�xi�Ō����\�ʂ���o�˂���B���̍ۂɁA�\�ʂɕ��s�Ȃ��ׂĂ̊i�q�ʂŋ��ʔ��˂����d�q�������ʑ��ŋ��ߍ����ꍇ�ɁA�d�q����܂��N����(���̎����ł͕\�ʂł̔��˂ɂ�����ʑ��̔��]�͋N����Ȃ�)�B�����̕\�ʂɕ��s�Ȋi�q�ʂ̊Ԋu��d�C�v�����N�萔��h�C�d�q�̎��ʂ�m�C�d�q�̓d�ׂ�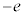 (
(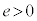 )�Ƃ��Ĉȉ��̖₢�ɓ�����B
)�Ƃ��Ĉȉ��̖₢�ɓ�����B
(d) �d�q�̗��q�Ƃ��Ă̑����ɂ��āA�^�ɂ�����l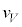 �ƁA�������ɂ�����l
�ƁA�������ɂ�����l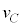 ���Ah�Cm�Ce�CV�C
���Ah�Cm�Ce�CV�C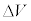 �̒�����K�v�Ȃ��̂�p���ĕ\���B
�̒�����K�v�Ȃ��̂�p���ĕ\���B
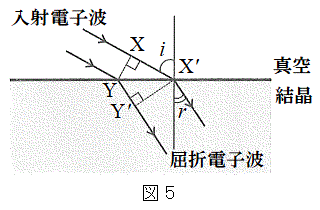 (f) �}5�̂悤�ɓ��˓d�q�g��Y�ɓ��B�����Ƃ��̔g��XY���A���ܓd�q�g�̔g��
(f) �}5�̂悤�ɓ��˓d�q�g��Y�ɓ��B�����Ƃ��̔g��XY���A���ܓd�q�g�̔g��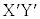 �ւƐi�ލۂɁA�^�ł̌o�H
�ւƐi�ލۂɁA�^�ł̌o�H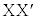 �ɂ�����ʑ��ω��ƌ������̌o�H
�ɂ�����ʑ��ω��ƌ������̌o�H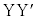 �ɂ�����ʑ��ω��͓������B���̂��Ƃ𗘗p���āA�d�q�����^�猋���ɓ��˂���Ƃ��̋��ܗ�
�ɂ�����ʑ��ω��͓������B���̂��Ƃ𗘗p���āA�d�q�����^�猋���ɓ��˂���Ƃ��̋��ܗ�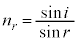 ���Ah�Cm�Ce�CV�C
���Ah�Cm�Ce�CV�C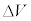 �̒�����K�v�Ȃ��̂�p���ĕ\���B�������A�d�q�̗��q�Ƃ��Đi�ޑ����Ɠd�q�g�̔g�ʂ��i�ޑ����͈قȂ�A
�̒�����K�v�Ȃ��̂�p���ĕ\���B�������A�d�q�̗��q�Ƃ��Đi�ޑ����Ɠd�q�g�̔g�ʂ��i�ޑ����͈قȂ�A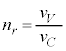 �Ƃ͂Ȃ�Ȃ��B
�Ƃ͂Ȃ�Ȃ��B
(g) �^�ƌ������ŁA�d�q�̗��q�Ƃ��Ẳ^���ʂ��ǂ��ω����������l����B�������ŁA�d�q�̗��q�Ƃ��Ẳ^�����ϑ������Ƃ���A��(f)�̋��ܓd�q�g�Ɠ��������ɉ^�����Ă��邱�Ƃ����������B�������̉^���ʂ́A�\�ʂɕ��s�Ȑ����̑傫��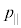 �ƁA�\�ʂɐ����Ȑ����̑傫��
�ƁA�\�ʂɐ����Ȑ����̑傫��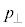 ���A
���A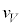 ��i ��K���܂߁Ah�Cm�Ce�C
��i ��K���܂߁Ah�Cm�Ce�C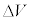 �̒�����K�v�Ȃ��̂�p���ĕ\���B
�̒�����K�v�Ȃ��̂�p���ĕ\���B
(h) ���낢��ȉ����d��V�ł������d�q����p���āA������ˊpi �Ɣ��ˊpi �œd�q����܂��N�������ǂ����ׂ��Ƃ���A������V�ɂ����ĉ�����������Ƃ����������B���������V���Ah�Cm�Ce�Cd�C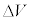 �Ci�C����n�̒�����K�v�Ȃ��̂�p���ĕ\���B�������A�������݂��邽�߂�n�̏����͓����Ȃ��Ă悢�B
�Ci�C����n�̒�����K�v�Ȃ��̂�p���ĕ\���B�������A�������݂��邽�߂�n�̏����͓����Ȃ��Ă悢�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@[A]��X����܂Ɠ��l�ɍl���܂��B�ڐV�������œr�������������������ɂȂ�܂����A���@�藝�̌�����������Ă���̂ŁA������q���g�ɍl���܂��傤�B[B]�́A(h)�������̊����Ɠ��l�ɍl���܂����A(f)�́u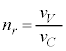 �Ƃ͂Ȃ�Ȃ��v�ɒ��ӂ��K�v�ł��B�I�Ղ́A�g���镶���̐����̂��߂ɁA�v�Z�����G�ɂȂ�܂��B
�Ƃ͂Ȃ�Ȃ��v�ɒ��ӂ��K�v�ł��B�I�Ղ́A�g���镶���̐����̂��߂ɁA�v�Z�����G�ɂȂ�܂��B
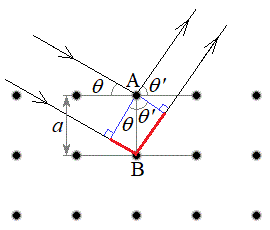 [A](a) �E�}���AA�ŎU�����ꂽX����B�ŎU�����ꂽX���̌o�H��(�Ԑ�����)��
[A](a) �E�}���AA�ŎU�����ꂽX����B�ŎU�����ꂽX���̌o�H��(�Ԑ�����)��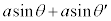 �C����āA�o�H����
�C����āA�o�H����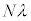 �ƂȂ�ꍇ�A
�ƂȂ�ꍇ�A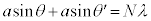 (N��1�ȏ�̐���)��
(N��1�ȏ�̐���)�� 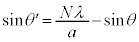 ......[��]�@����@
......[��]�@����@
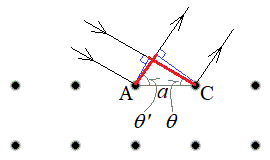 (b) �E�}���AA�ŎU�����ꂽX����C�ŎU�����ꂽX���̌o�H����
(b) �E�}���AA�ŎU�����ꂽX����C�ŎU�����ꂽX���̌o�H����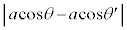 �C����āA�o�H����
�C����āA�o�H����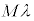 �ƂȂ�ꍇ�A
�ƂȂ�ꍇ�A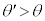 �C����
�C����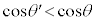 �̂Ƃ�
�̂Ƃ�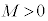 ���A
���A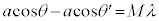 (M�͐���)��
(M�͐���)�� 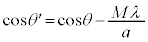 ......[��]�@����A
......[��]�@����A
����ć@��������́A
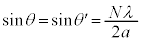 ......[�A]
......[�A]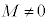 �̂Ƃ��A�}3���A
�̂Ƃ��A�}3���A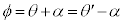 �C��蕶�������@�藝�̌������A
�C��蕶�������@�藝�̌������A�@�C�A��������ƁA
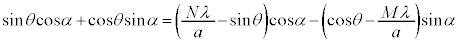
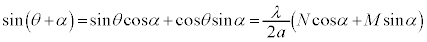 �@����B
�@����B�܂��A���l�ɇ@�C�A��p���āA
�� 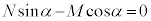 �C
�C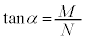 ......[�C]
......[�C] 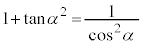 ���A
���A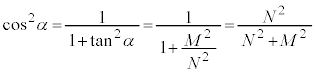
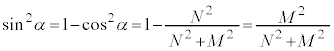
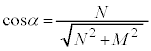 �C
�C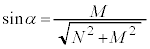 �@(�
�@(�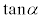 �C
�C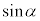 �CM�̕�������v���邱�Ƃɒ���)
�CM�̕�������v���邱�Ƃɒ���)�B�ɑ������ƁA������́A
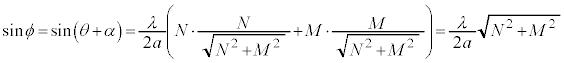 ......[�E]
......[�E]
[B](d) �����d��V���d�q1�ɗ^����G�l���M�[��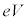 �C���ꂪ�d�q�̉^���G�l���M�[
�C���ꂪ�d�q�̉^���G�l���M�[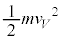 �ɂȂ�̂�(�d�q���Q��)�A
�ɂȂ�̂�(�d�q���Q��)�A 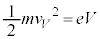 �@����C
�@����C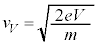 ......[��]
......[��]�d�q�͌������̐��̓d��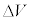 �ɂ���ĉ�������܂��B
�ɂ���ĉ�������܂��B 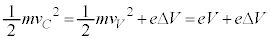 �@����D
�@����D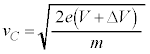 ......[��]
......[��]
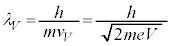 ......[��]�C
......[��]�C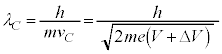 ......[��]
......[��]
(f) �ʑ��ω����������ƌ����Ă��A�d�q�g�̐U������f �Ƃ��āA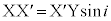 �C
�C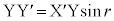 ��ʉ߂��鎞�Ԃ��l���āA
��ʉ߂��鎞�Ԃ��l���āA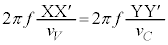 �Ƃ���̂ł́A
�Ƃ���̂ł́A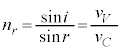 �ƂȂ��Ă��܂����s���܂��B�����œd�q�g�̔g���̕����l���܂��B
�ƂȂ��Ă��܂����s���܂��B�����œd�q�g�̔g���̕����l���܂��B 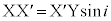 �C
�C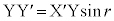 �̒��ɓ���g�̐����l���A�ʑ��ω����������Ƃ���(�ʑ����Q��)�A
�̒��ɓ���g�̐����l���A�ʑ��ω����������Ƃ���(�ʑ����Q��)�A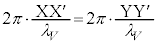 �@����E
�@����E(e)�̌��ʂ�p���āA
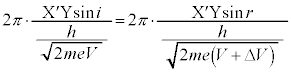 �@��
�@�� 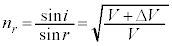 ......[��]
......[��]������A
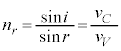 �@����F
�@����F�ƂȂ��Ă��邱�Ƃ�������܂��B
(g) �d�q�̗��q�Ƃ��Ẳ^�������́A��(f)�̋��ܓd�q�g�Ɠ��������Ȃ̂ŁA���������^����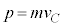 �́A�\�ʂɕ��s�Ȑ�����
�́A�\�ʂɕ��s�Ȑ�����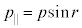 �C�\�ʂɐ����Ȑ�����
�C�\�ʂɐ����Ȑ�����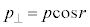 �ł��Bi�C
�ł��Bi�C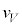 �C
�C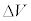 �͉Ɏg���܂����Ar�C
�͉Ɏg���܂����Ar�C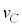 �CV�͎g���܂���B�F��p����ƁA
�CV�͎g���܂���B�F��p����ƁA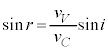 �@����G
�@����G 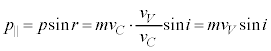 ......[��]
......[��]�D���A
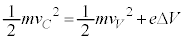 �@��
�@�� 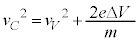 �@����H
�@����H�G��p���āA
�H��p���āA
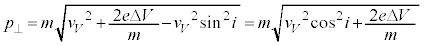 ......[��]
......[��]
 (h) �E�}���o�H��(�Ԑ�����)��
(h) �E�}���o�H��(�Ԑ�����)��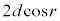 �ɂȂ�܂��B�����ł́AV�����߂����̂ŁA(f)�̌��ʂ����̂܂g���܂��B
�ɂȂ�܂��B�����ł́AV�����߂����̂ŁA(f)�̌��ʂ����̂܂g���܂��B������́A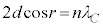 (n�F����)���A(e)�̌��ʂ�p���āA
(n�F����)���A(e)�̌��ʂ�p���āA ���ӂ�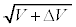 ��������2�悷��ƁA
��������2�悷��ƁA
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 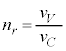 �Ƃ͂Ȃ�Ȃ��B
�Ƃ͂Ȃ�Ȃ��B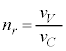 �Ƃ͂Ȃ�Ȃ��v�ɒ��ӂ��K�v�ł��B�I�Ղ́A�g���镶���̐����̂��߂ɁA�v�Z�����G�ɂȂ�܂��B
�Ƃ͂Ȃ�Ȃ��v�ɒ��ӂ��K�v�ł��B�I�Ղ́A�g���镶���̐����̂��߂ɁA�v�Z�����G�ɂȂ�܂��B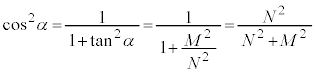
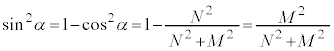
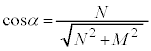 �C
�C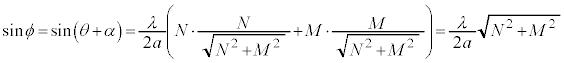 ......[�E]
......[�E]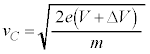 ......[��]
......[��]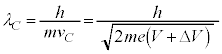 ......[��]
......[��]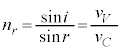 �ƂȂ��Ă��܂����s���܂��B�����œd�q�g�̔g���̕����l���܂��B
�ƂȂ��Ă��܂����s���܂��B�����œd�q�g�̔g���̕����l���܂��B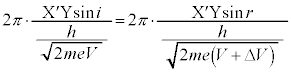 �@��
�@�� 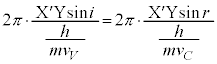
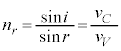 �@����F
�@����F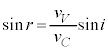 �@����G
�@����G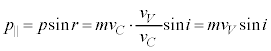 ......[��]
......[��]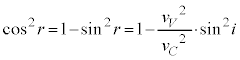
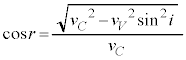
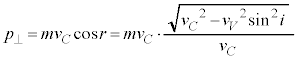
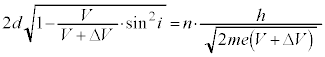
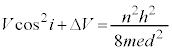
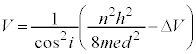 ......[��]
......[��]