東大物理'02年前期[3]
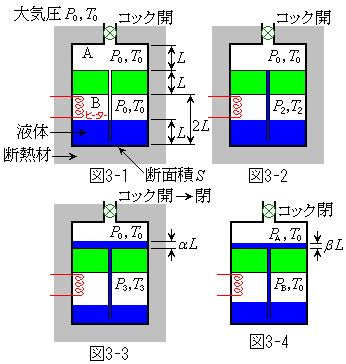図3-1に示すような円筒形の容器が断熱材におおわれ鉛直に置かれている。容器は厚さLの断熱材が詰め込まれた壁でA室，B室二つの部屋に仕切られている。円筒内部の断面積をS，A室の高さをL，B室の高さを
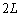とする。また、容器の上面には大きさの無視できるコックがつけられており、A室とB室の間は容積の無視できる細管でつながれている。また、B室の上方の空間にはヒーターが取り付けられている。最初、図3-1では、コックは開いており、B室に密度ρの液体が、底面から高さLのところまで満たされている。A室とB室それぞれの空間には、大気圧
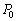と室温
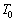に等しい圧力と温度の単原子分子理想気体が満たされている。液体の蒸発、及び気体と液体の間での熱の出入りは無視できるものとする。重力加速度をgとして以下の問に答えよ。
Ⅰ コックは開いたまま、ヒーターのスイッチを入れると、B室内の気体は加熱されて圧力が上がり、液体が細管を伝わってA室に向かい移動をはじめた。A室の底に液面が達した時の状態を図3-2に示す。この間のB室内気体の状態変化は、定積変化として近似できるものとする。
(1) B室の液面の高さでの液体に働く力のつり合いを考えることにより、図3-2の状態でのB室内気体の圧力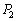
を、ρ，g，L，
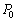を用いて表せ。 (2) 図3-2の状態にいたるまでにヒーターからB室内の気体に加えられた熱量Qをρ，g，L，Sを用いて表せ。
Ⅱ 加熱を続けると、液体はさらに移動し、ヒーターのスイッチを切った後、A室内の液面の高さを測定したところ、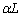
であった。この状態を図3-3に示す。 (1) 図3-3の状態でのB室内の圧力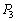
とする。この時のB室内の気体の温度
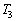を、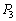
，
，
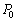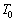，αを用いて表せ。 (2) 図3-1から図3-3の過程における、B室内の気体の状態の変化を、縦軸を圧力、横軸を体積とするグラフで示せ。
(3) B室内の気体がした仕事Wを、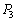
，
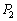，S，L，αを用いて表せ。
Ⅲ 図3-3の状態でコックを閉じ、容器をおおっていた断熱材を取り除いた。十分時間が経って、中の気体の温度が室温と同じになったとき、A室内の液面の高さを測定したところ、図3-4のように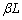
であった。 (1) 図3-4の状態で、A室、B室それぞれにおける気体の圧力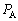
，
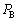を、α，β，
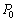を用いて表せ。 (2) αを、β，ρ，g，L，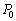
を用いて表せ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 難しそうに見えますが、親切な誘導がついているので、最後まで何とかたどりつけるでしょう。途中、Ⅱ(2)などに気づきにくい部分もありますが、バネつきピストンの問題と同じように考えて、PとVの関係を求めればよいのです。密度については、浮力も参考にしてください。
Ⅰ(1) 細管の断面積を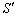
とします。B室の液面の高さから上の部分にある細管内の液体の体積は
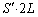，この部分の液体の質量
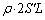が受ける重力は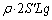
B室の液面の高さで、液体が受ける力は、A室の気体が押す鉛直下向きの力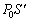
，液体が受ける鉛直下向きの重力
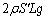，液体下部の液面が押す鉛直上向きの力
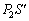です。これらの力のつり合いより、 ∴ 
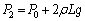......[答] ･･･①
(2) 図3-1の状態において、B室に気体がnモルあるとして、B室の気体の占有体積は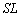
だから、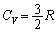 
，
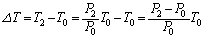
として、
ここで、②を使うと、
ここで、①を使うと、
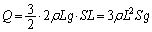......[答]
Ⅱ(1) B室の気体の体積は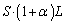
図3-2における状態方程式：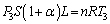
･･･④
④÷②より、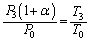
∴ 
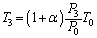......[答]
(2) B室の液面の高さから上の部分にある細管内の液体の体積は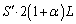
(右図参照)，この部分の液体の質量
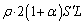が受ける重力は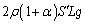
B室の液面の高さで、液体が受ける力は、A室の気体が押す鉛直下向きの力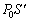
，液体が受ける鉛直下向きの重力
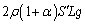，液体下部の液面が押す鉛直上向きの力
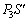です。これらの力のつり合いより、 ∴ 
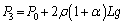･･･⑤B室の気体の体積をVとして、 ∴ 
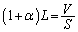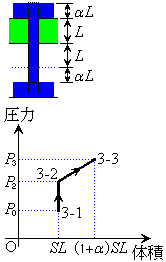
これを⑤に代入すると、 この式から、図3-2の状態より図3-3の状態まで、B室の気体の変化のpV図は、直線になることがわかります。
よって、図3-1から図3-3の過程における、B室内の気体の状態の変化は、右図。
(3) (2)のpV図で、図3-2の状態から図3-3の状態までの変化を表す線分とV軸で挟まれた台形部分の面積が、B室の気体のした仕事になります。 求める仕事：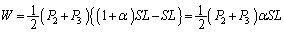
......[答]
Ⅲ(1) コックを閉める前に、A室の気体が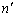
モルあったとして、A室の気体の占有体積は
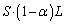だから、
(2) 図3-4の状態における力のつり合いの式は、⑤式で、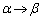
，
，
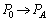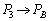としたものです。 ∴ 
∴ 
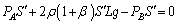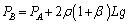
(1)の結果を代入し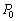て、 
で割って、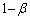
をかけると、∴ 
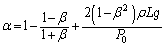
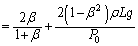......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東大物理TOP 物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
･･･②
として、
･･･③
(モル比熱を参照)において、単原子分子理想気体なので
･･･⑥
だから、
･･･⑦
......[答]
だから、状態方程式：
･･･⑧
......[答]
