東京大学2009年前期物理入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
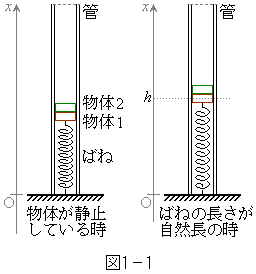[1] 図1－1のように、鉛直に固定した透明な管がある。ばね定数kのばねの下端を管の底面に固定し、上端を質量mの物体1に接続する。質量が同じくmの物体2を、物体1の上に固定せずに乗せる。地面上の一点Oを原点として鉛直上向きにx軸をとる。ばねが自然長になっているときの物体1のx座標はhであり、重力加速度の大きさはgである。
なお、物体の大きさは小さく、管との摩擦や空気抵抗は無視でき、x方向以外の運動は考えない。ばねの質量は無視できる。また、管は十分長く、実験中に物体が飛び出すことはないものとする。
Ⅰ 物体1と物体2を、互いに接した状態で、物体1のx座標が
となる位置まで押し下げ、時刻
に初速度0で放したところ、物体1と物体2は互いに接した状態で単振動を開始した。 (1) この時の、物体1の単振動の中心のx座標を答えよ。
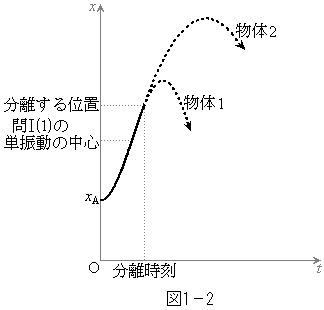(3) 
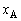の値によっては、運動中に物体1と物体2が分離することがある。図1－2はこのような場合の物体の位置の時間変化を示す。運動方程式を使って、分離の瞬間の物体1のx座標を求めよ。なお、図1－2では物体の大きさは無視されており、接している間の物体1と物体2の位置を1本の実線で表している。(4) 分離の瞬間の物体1の速度を答えよ。また、分離が起きるのは、時刻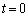
における物体1の位置
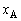がどのような条件を満たす場合か答えよ。 Ⅱ 物体1と物体2が分離した後の運動について考える。分離後、物体1は単独で単振動する。物体2は重力のために、分離後ある時間が経過した後に必ず物体1に衝突する。分離から衝突までの時間は時刻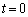
における物体1の位置
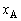に依存する。ここで、分離から衝突までの時間が、物体1が単独で単振動する際の周期Tに等しくなるように、
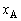の値を設定した。衝突の時刻を
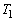とする。 (1) 物体1が単独で単振動する際の周期Tを答えよ。また、物体1と物体2が衝突する瞬間(時刻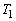
)の物体1のx座標を答えよ。 (2) 分離の瞬間の物体2の速度をVとする。分離から衝突までの時間がTとなるためのVの満たす式を書け。
(3) 物体1と物体2の間のはねかえり係数は1であるとし、時刻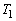
における衝突以降の運動を考える。物体1と物体2が、
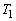以降に再び接触する時刻
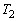と、そのときの物体1のx座標を答えよ。また、時刻
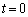から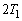
までの間で、横軸を時刻、縦軸を物体の位置とするグラフの概形を描け。物体の大きさは無視し、物体1と物体2が接した状態で運動している部分は実線、分離している部分は点線を用いよ。なお、横軸、縦軸ともに、値や式を記入する必要はない。 (4) この場合の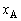
をh，m，k，gを用いて表せ。 [解答へ]
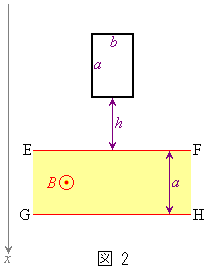[2] 図2のように、紙面内の上から下向き(x軸の正の向き)に重力(重力加速度の大きさg)がはたらき、紙面に垂直に裏から表の向きに一様な磁場(磁束密度の大きさB)が、EFとGHの間の領域だけに加えられている。EFとGHは水平である。抵抗R，質量mの一様な導線を一巻きにして作った高さa，幅bの長方形のコイルABCDを、磁場のある領域の上方から落下させる。その際、ABCDは紙面内にあり、BCがx軸と平行となるように、常に姿勢を保つようにした。EFとGHの距離はコイルの高さaに等しい。導線の太さはaやbに比べ十分小さく、EFはbに比べ十分長いものとする。また、自己誘導や空気抵抗は無視し、地面との衝突は考えないものとする。
Ⅰ 時刻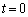
に、ABとEFの距離がhとなる位置から初速度0でコイルを落下させた。 (1) ABがEFに到達する時刻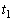
と、その時のコイルの速さ
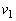をhを用いて表せ。 (2) ABがGHに到達する時刻を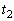
とする。ある時刻t (
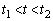)に、コイルが速さvで落下しているとする。このとき、コイルにはたらく合力(x軸の正の向きを正とする)をvを用いて表せ。 (3) ABがEFに到達する時のコイルの速さ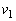
の値によって、時刻
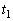から
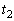の間にコイルが加速する場合と減速する場合がある。それぞれの場合における、
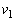の条件を記せ。 Ⅱ 時刻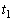
から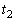
の間コイルが等速度で落下するように、時刻
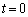におけるコイルの位置をうまく調整してから、初速度0で落下させた。 (1) この場合の、時刻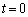
におけるABとEFの距離と時間
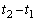を求めよ。 (2) 時刻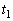
から
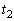の間に、コイルで消費される電力Pと熱として発生するエネルギーWを求めよ。 [解答へ]
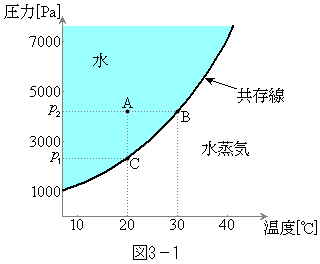[3] 常温の水は液体(以後単に水という)と気体(水蒸気)の2つの状態をとることができる。どちらの状態をとるかは温度と圧力により、図3－１に示すように定まる。たとえば、水をシリンダーに密封して温度を
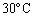，圧力を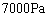
にしたときは水であり、熱を与えて、温度や圧力を多少変えても全部が水のままである。一方、同じ
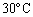で、圧力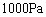
にしたときはすべて水蒸気である。ただし、図3－1のB点、C点のような境界線上の温度と圧力のときは水と水蒸気が共存できる。逆に、水と水蒸気が共存しているときの温度と圧力はこの境界線(共存線)上の値をもつ。温度を与えたときに定まる共存時の圧力を、その温度での蒸気圧という。一定の圧力で共存している水と水蒸気に熱を与えると、温度は変わらずに、熱に比例する量の水が水蒸気に変わり、全体の体積は膨張する。単位物質量の水を水蒸気に変化させるために必要なエネルギーを蒸発熱と呼ぶ。
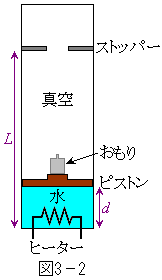このことを参考にして、図3－2に示す装置のはたらきを調べよう。断面積
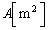で下端を閉じたシリンダーを鉛直に立てて、物質量
の水を入れ、質量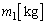
のピストンで密閉し、その上に質量
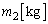のおもりを乗せる。シリンダーの上端を閉じてピストンの上側を真空にする。ピストンはシリンダーと密着してなめらかに動くことができるが、シリンダーの上方にはストッパーが付いていて、ピストンの下面の高さが
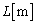になるところまでしか上昇しないようになっている。シリンダーの底にはヒーターが置かれていて、外部からの電流でジュール熱を発生できるようになっている。以下の過程を通じて、各瞬間の水と水蒸気の温度はシリンダー内の位置によらず等しいものとする。また、圧力の位置による違いは無視する。
Ⅰ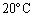 
での蒸気圧を
，
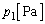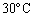での蒸気圧を
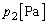と記す。ピストンのみでおもりを乗せないときに内部の圧力が
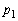で、ピストンにおもりを乗せたときに
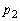になるようにしたい。
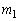と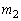
を求めよ。重力加速度の大きさを
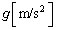とする。 Ⅱ 圧力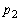
での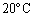
の水のモル体積(
当たりの体積)を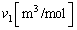
とする。この温度でおもりをのせた状態でのシリンダー内の水の深さ
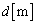を求めよ。なお、ヒーターの体積は無視できる。 
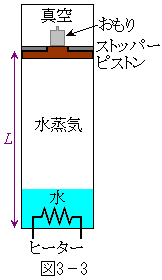Ⅳ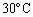 
の水をさらにヒーターでゆっくりと加熱する。このときの温度と圧力はB点に留まり、水は少しずつ水蒸気に変化していく。図3－3のようにピストンがストッパーに達したときにも水が残っていた。B点での水のモル体積
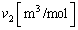とB点での水蒸気のモル体積
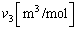を用いて、このときの水蒸気の物質量
を求めよ。Ⅴ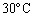 
の水を、その温度での蒸気圧の下で、水蒸気にするために必要となる蒸発熱を
とする。問Ⅳの過程で、ピストンがストッパーに達するまでに、ヒーターで発生させるジュール熱
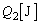を求めよ。 Ⅵ ピストンがストッパーに達したときにヒーターを切り、おもりを横にずらして、ストッパーに乗せる。次にまわりの断熱材を取り除き、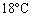
の室内で装置全体がゆっくり冷えるのを待つ。 (1) 時間の経過(温度の低下)とともに、圧力がどのように変化するか述べよ。
(2) 時間の経過(温度の低下)とともに、ピストンはストッパーに接した位置と水面に接した位置の間でどのように動くか、動く場合にはその速さ(瞬間的か、ゆっくりか)を含めて述べよ。 [解答へ]
各問検討
[1](解答はこちら) 本問は力学の総合問題で、単振動と等加速度運動に、分離、衝突、エネルギーがからんだ問題です。決して難しい問題とは言えないのですが、さりとて、物理を得意科目にしていない高校生にとっては、気が遠くなるような印象を受けてしまうかも知れません。
私が持っている物理Ⅰの教科書は、「電気」から記述が始まっているのですが、物理の入試準備を始めるときには、「力学」から始めるべきです。物理の勉強を「電気」から始めるのは全くナンセンスです。物理学の基本を文科省のお役人さんの都合で歪めて良いわけがないのです。そして、まず最初に、本問のような力学の総合問題を解けるように努力するべきです。
本問は、グラフを描かせる部分など、全体を通して眺めると、いろいろな入試問題を解いた経験を要求していて、それなりのレベルなのですが、個々の部分を取り出すと、実は、基本レベルの寄せ集めでしかありません。決して高度な受験技巧を要求しているわけではないのです。
運動方程式を書いて単振動の周期を求めたり、垂直抗力を求めて分離する条件を考えたり、力学的エネルギー保存の式を立てたり、ということの一つ一つは、教科書の例題レベルの内容です。各学校で配布される物理の基礎問題集の練習問題を一題ずつ解いていくのと、ほとんど変わりはありません。引っかかる点があれば、物理Ⅰ、物理Ⅱの教科書の関連事項のところをまず熟読してください。「力学」の基礎固めをする間は参考書は不要です。高校生にとって物理を縁遠く感じさせてしまう原因は、教科書に書かれている基礎事項の習得が不足している点にあります。まずは、教科書で基礎知識をしっかり身につけてください。
本問は、同じ質量の物体が完全弾性衝突(反発係数が1)をすると速度を交換する、従って、衝突の時点を境にして、2物体の運動は完全に対称になる、ということが全体的なストーリーの流れになっています。物理を得意とする受験生は、問題文を眺めただけで、運動の状況(従って、Ⅱ(3)のグラフ)を頭の中にイメージすることができるだろうと思います。ですが、基礎的な勉強を積み重ねている間は、質量mの物体1と物体2が速度vと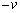
で向かい合って進んで来て、衝突した後の速度を求めるとき、以下のように、運動量保存則の式と反発係数の式を連立するので構いません。
衝突後の物体1，物体2の速度をu，wとして、
運動量保存より、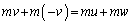
･･･①
反発係数の式：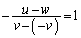
･･･②
①より、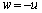
②に代入して、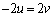
∴ 
，
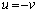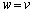
これで、物体1と物体2の速度が衝突前後で入れ替わることがわかります。しかし、こうしたことは、いろいろと入試問題を解いてくると、覚えようとしなくても自然に記憶されて、問題文を読んだだけで、多分、こうなるんだろう、という経験的予測が立つようになってきます。こうなるまでは、忍耐して、教科書や基礎的問題集の反復練習を行ってください。ここが苦しくて物理離れを起こす高校生が多いのですが、逆に言うと、ここを乗り切れれば、物理は、入試科目の中で最もラクな科目です。最小の努力で最大の得点を稼ぐことのできる科目です。安易にもうけ話に乗って大事な貯金を巻き上げられてしまうお気の毒な高齢者のニュースをよく耳にしますが、安易なもうけ話に乗ってはいけない、ということはどういうことかと言うと、辛そうな道の向こうにこそ花咲き乱れる楽園がある、ということなのです。
[2](解答はこちら) よく勉強してきた受験生にとっては何の変哲もない標準問題、という本問でも、これから受験勉強を始めようという人にとっては、なかなか厳しい問題です。数学に比べて物理は努力しても努力してもなかなか結果が出てこなくて結局息切れしてしまう、という受験生の声をよく聞きます。その原因は、本問のような問題では、電磁気の広範な分野に渡ってしっかり理解ができていないと大問1題を完答することができない、というところにあると思います。
本問では、磁束、電磁誘導の法則、レンツの法則、フレミング左手の法則・右手の法則、電力などの基礎事項を理解できているか、さらに付け加えて、磁場中を通過するコイルの運動が、終端速度に漸近する雨滴の運動と同様になる、ということを様々な問題を解く中で経験的に知っているか、ということが問われています。こうしたことは、1週間程度、物理の教科書を読んで基礎的な問題集に載っている単発的な問題を解いてみた、というくらいでは、なかなか厳しいものがあるのです。従って、結果にすぐ表れないからと言って短気を起こしてはいけません。地道にコツコツと努力を続けていく必要があります。
本ウェブサイトでは、多数の過去問を掲載しています。できる限り多くの過去問に触れて頂きたいと思います。そして、過去問を見ていくときに、そこに貼られているリンクを一つずつたどりながら、基礎事項がどのように入試問題で使われているのか丹念にたどってみて頂きたいのです。こうした努力を続けているうちに、電磁気の基礎事項が一通り体得できて、それらの関連性などが把握できたところで、ある日突然、なんだ、この問題、簡単なんだなあ、と、思える日がやってきます。
教科書を一通り読んだ程度では、東大・東工大・京大などの過去問を自力で解こうとしても、どこから手を付ければよいのやら、ということになると思うので、最初から本ウェブサイトの解答を読んでしまうので構いません。本問であれば、磁束を求め、電磁誘導の法則から起電力を、オームの法則から電流を、さらに公式：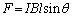
から導線に働く電磁力の大きさを、フレミング左手の法則より電磁力の向きを求めて行く、というのは、定型的な流れなので、この流れに沿って基礎事項をマスターできればよいのです。
また、難関国立大などとても、という方でも、まず教科書をしっかり理解して、本ウェブサイトの解答を追いながら基礎事項の理解を深めて頂ければ、難関国立大のレベルは誰にでも手の届くところにあるのです。高い目標と強い意志をもって頑張って頂きたいと思います。
[3](解答はこちら) 2009年の東大物理の問題は、第1問と第2問が力学、電磁気の基本を見る問題、第3問が発展的な問題となっています。発展的とは言っても、数学の第6問とは異なり、教科書の内容に即して物理的な思考能力を見るようになっていて、決して無理な問題ではありません。ふだんから自然現象に関心を持って、どうしてこうなるんだろう、と、考えることの好きな物理少年であれば、楽しく考えられるような問題に工夫されています。問題を解くに当たって必要となる基礎事項は、力のつり合い、比熱の式、くらいなものです。気体分野の問題なのに状態方程式でさえ必要となりません。ⅠからⅤまでは、Ⅵを考えるためのヒントになっていて、考え込むような部分はありません。自然にⅥに進むようにうまく誘導されています。
さて、Ⅵですが、こうした問題では、あくまで、問題文の内容に即して考える、という点に注意しましょう。仮に、独学でより進んだ知識を持っていたとしても、その知識を使うと、問題文が想定している条件と異なってしまうかも知れないからです。また、自然現象の事実と仮に異なるとしても、自然現象に合わせて解答するのではなく、問題文の条件に即した結論を答えるようにしてください。本問であれば、問題文に与えられている蒸気圧曲線を用いて、「水は少しずつ水蒸気に変化していく」という問題文の記述に合わせて考える必要があります。
また、問題文に想定されている条件にかなり無理な部分があっても、その条件設定を問題視してはいけません。入試問題で条件設定を変えると、多くの場合、高校の範囲を超えるような数学の技巧が必要になってしまうのです。問題文が要求しているレベルに合わせて解答するようにします。
なお、解答には書いてありませんが、温度が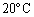
から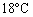
まで変わるときの水の体積変化を考慮すると、この間にもピストンは静止せずに下がり続けるのではないか、と、お考えの方もいると思います。ですが、水の熱膨張係数は
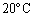では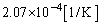
と非常に小さく、温度が変化しても体積はほぼ一定です。ちなみに、水は
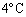において熱膨張係数が0となり、
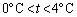の範囲の温度tにおいては、 熱膨張係数は負です。従って、風呂の湯を温めているときには、水中から水面に上昇するに従って水温が高くなりますが、氷が張っている池では氷の張っている表面のところが最も温度が低く、水中から上昇するに従って水温が低くなります。この辺は、インターネット上でも議論があるところで、興味を持たれた方は、「水 熱膨張係数」で検索してみてください。東大の出題者が
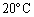から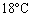
までという温度を選んでいるのも、インターネット上の議論を参考にしたのではないか、という気がします。今後は、大学受験する場合は、ネット上での議論にも目を光らせる必要がある、ということです。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東大物理TOP 物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
，
，物体1の位置をx，互いに及ぼす抗力の大きさをN (
)とせよ。
とする。時間
を求めよ。また、落下開始から、磁場のある領域を十分離脱するまでの、コイルの速さの時間変化を表すグラフを描け。グラフには、
(具体的な式は不要)と、それらの時刻における速さの式を記せ。
であった水をヒーターでゆっくりと
になるまで加熱する。このとき、水の状態は図3－1のA点からB点に移る。
から
までの水の定圧モル比熱は温度によらず、
であるとする。水を
にするためにヒーターで発生させるジュール熱
を求めよ。なお、シリンダー、ピストン、おもり、断熱材など、水以外の物体の熱容量は無視できるものとする。