���嗝�H����'09�N[2]
�ȉ��̖�̓����p���̉��ɋL������B
 ���C�Ȃ������s�X�g��
���C�Ȃ������s�X�g�� �C
�C ����������`�̗e��
����������`�̗e�� �C
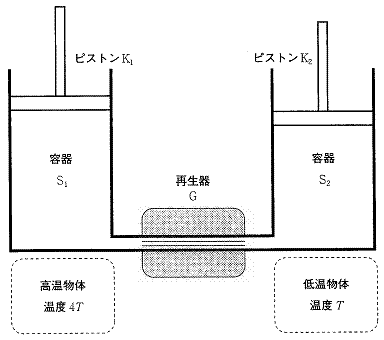
�C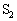 ��̐ς������ł���ׂ��p�C�v�łȂ��A�e��S�̂�1�����̒P���q���q���z�C�̂��������u(�}�Q��)�ɂ��čl���悤�B2�̗e��̓p�C�v�łȂ����Ă���̂ŁA�C�̂̈��͂͑��u���̂ǂ��ł�����ɂȂ�B
��̐ς������ł���ׂ��p�C�v�łȂ��A�e��S�̂�1�����̒P���q���q���z�C�̂��������u(�}�Q��)�ɂ��čl���悤�B2�̗e��̓p�C�v�łȂ����Ă���̂ŁA�C�̂̈��͂͑��u���̂ǂ��ł�����ɂȂ�B
�e��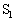 �͍������̂ɁA
�͍������̂ɁA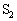 �͒ቷ���̂ɐڂ��A�e����̋C�̂̉��x�͂��ꂼ���Ή��x
�͒ቷ���̂ɐڂ��A�e����̋C�̂̉��x�͂��ꂼ���Ή��x �CT�ɕۂ���Ă���B�������́C�ቷ���̂Ɛڂ��Ă���ʂ������A�e�킨��уs�X�g���͔M��ʂ��Ȃ��f�ނłł��Ă���B
�CT�ɕۂ���Ă���B�������́C�ቷ���̂Ɛڂ��Ă���ʂ������A�e�킨��уs�X�g���͔M��ʂ��Ȃ��f�ނłł��Ă���B
�p�C�v�ɂ́A�e����̋C�̂Ƃ����M�����Ƃ肷��u�Đ���v�ƌĂ�鑕�uG���������Ă���B�Đ���G�̓G�l���M�[��~���Ă���A�e�� ����
����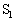 �Ɉړ�����C�̂����xT����
�Ɉړ�����C�̂����xT����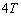 �ɉ��M�A
�ɉ��M�A ����
����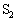 �Ɉړ�����C�̂�
�Ɉړ�����C�̂� ����T�ɗ�p���A���M���ɕ��o�����M���p���ɉ������B
����T�ɗ�p���A���M���ɕ��o�����M���p���ɉ������B
�}�̑��u�ɂ��Ď���4�̏�Ԃ��l���悤�B�������A�C�̒萔��R�Ƃ���B
���A�F�e��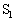 �C
�C ���̋C�̂̑̐ς�������V�ł�����(���̐ς�
���̋C�̂̑̐ς�������V�ł�����(���̐ς�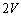 )�B���̂Ƃ��̑��u���̋C�̂̈��͂�
)�B���̂Ƃ��̑��u���̋C�̂̈��͂� �Ƃ���B
�Ƃ���B
���B�F�C�̂̈��͂����A�ƕς�炸 �ŁA���u���̋C�̂̑��̐ς�
�ŁA���u���̋C�̂̑��̐ς�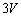 �ɂȂ�����ԁB
�ɂȂ�����ԁB
���C�F�C�̂̈��͂�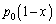 �ƂȂ�A���u���̋C�̂̑��̐ς����B�ƕς�炸
�ƂȂ�A���u���̋C�̂̑��̐ς����B�ƕς�炸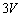 �̏�ԁB�������A����x��
�̏�ԁB�������A����x��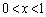 �����A���͂̕ω�����\���B
�����A���͂̕ω�����\���B
���D�F�C�̂̈��͂����C�ƕς�炸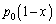 �ŁA���u���̋C�̂̑��̐ς�
�ŁA���u���̋C�̂̑��̐ς�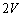 �ɂȂ�����ԁB
�ɂȂ�����ԁB
��1�@���A�̈���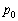 ���AT�CV�����R�ŕ\���B
���AT�CV�����R�ŕ\���B ��2�@���B�ɂ�����e��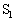 ���̋C�̂̑̐ς��AT�CV�CR�̂����K���Ȃ��̂�p���ĕ\���B
���̋C�̂̑̐ς��AT�CV�CR�̂����K���Ȃ��̂�p���ĕ\���B ��3�@���C�ɂ�����e�� ���̋C�̂̑̐ς��AT�CV�Cx�CR�̂����K���Ȃ��̂�p���ĕ\���B
���̋C�̂̑̐ς��AT�CV�Cx�CR�̂����K���Ȃ��̂�p���ĕ\���B ��4�@2�̃s�X�g�����ɂ������Ɠ������A���͂�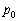 �ɕۂ��Ȃ���A���u�̏�Ԃ�A����B�ɕς���B���̂Ƃ��A���u�S�̂��O�ɂ����d��
�ɕۂ��Ȃ���A���u�̏�Ԃ�A����B�ɕς���B���̂Ƃ��A���u�S�̂��O�ɂ����d�� ����уs�X�g��
����уs�X�g�� �ɋC�̂������d��
�ɋC�̂������d�� ���AT�CV�Cx�CR�̂����K���Ȃ��̂�p���ĕ\���B
���AT�CV�Cx�CR�̂����K���Ȃ��̂�p���ĕ\���B ��5�@2�̃s�X�g�����ɂ�����蓮�����A���̐ς� �ɕۂ��Ȃ���A���u�̏�Ԃ�B����C�ɕς���B���̍ۂɑ��u�S�̂��O�ɂ����d��
�ɕۂ��Ȃ���A���u�̏�Ԃ�B����C�ɕς���B���̍ۂɑ��u�S�̂��O�ɂ����d�� ����уs�X�g��
����уs�X�g�� �ɋC�̂������d��
�ɋC�̂������d��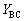 ���AT�CV�Cx�CR�̂����K���Ȃ��̂�p���ĕ\���B�������Ax��1���\���������Ƃ���B�K�v������A�C�̂̑̐ϕω�
���AT�CV�Cx�CR�̂����K���Ȃ��̂�p���ĕ\���B�������Ax��1���\���������Ƃ���B�K�v������A�C�̂̑̐ϕω�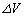 ���������Ƃ��ɋC�̂������d���́A�ω��O�̈���p��p����
���������Ƃ��ɋC�̂������d���́A�ω��O�̈���p��p����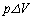 �Ɨ^�����邱�Ƃ𗘗p����B
�Ɨ^�����邱�Ƃ𗘗p����B
���u�̏�Ԃ��A���͂����ɕۂ��Ȃ���A����B�C���̐ς����ɕۂ��Ȃ���B����C�C�Ăш��͂����ɕۂ��Ȃ���C����D�ɂ������ς��A����ɑ��̐ς����ɂ���D����A�ɂ������Ɩ߂��ߒ����T�C�N��A��B��C��D��A�ƌĂڂ��B���̃T�C�N���ɂ��čl���悤�B
��6�@���͂̕ω���x��1���\���������Ƃ���B���u�̏�Ԃ��T�C�N��A��B��C��D��A�ɏ]���ĕω�������Ƃ��A���u�S�̂��O�ɂ����d��W����уs�X�g��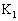 �ɋC�̂������d��Y���AT�CV�Cx�CR�̂����K���Ȃ��̂�p���A
�ɋC�̂������d��Y���AT�CV�Cx�CR�̂����K���Ȃ��̂�p���A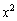 �ɔ�Ⴗ�鍀�����ċ��߂�B�K�v������A�ߎ���
�ɔ�Ⴗ�鍀�����ċ��߂�B�K�v������A�ߎ��� (�������Aa�Cb�͒萔)��p����B
(�������Aa�Cb�͒萔)��p����B ��7�@���u�̏�Ԃ��T�C�N��A��B��C��D��A�ɏ]���ĕω�������Ƃ��A���u���������̂�����M��Q�����߂悤�B�Đ���̓����̂��߁A��A�̏�ԕω��̍ۂɁA�e��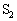 ����
����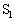 �Ɉړ������C�̗̂ʂƁA�e��
�Ɉړ������C�̗̂ʂƁA�e�� ����
���� �Ɉړ������C�̗̂ʂ��������Ƃ��A�e��
�Ɉړ������C�̗̂ʂ��������Ƃ��A�e��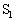 ���̋C�̂��e��
���̋C�̂��e�� ���̋C�̂���эĐ���G������M�ʂƁA
���̋C�̂���эĐ���G������M�ʂƁA ���̋C�̂�
���̋C�̂�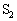 ���̋C�̂����G�ɕ��o����M�ʂ͓������B���̂��ƂƔM�͊w�̑��@���𗘗p���A�M��Q���A
���̋C�̂����G�ɕ��o����M�ʂ͓������B���̂��ƂƔM�͊w�̑��@���𗘗p���A�M��Q���A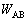 �C
�C �C
�C �CW�C
�CW�C �C
�C �C
�C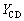 �CY�̂����K���Ȃ��̂�p���ĕ\���B�������A��ԕω�C��D�ɔ������u�S�̂��O�ɂ����d����
�CY�̂����K���Ȃ��̂�p���ĕ\���B�������A��ԕω�C��D�ɔ������u�S�̂��O�ɂ����d����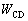 �C�s�X�g��
�C�s�X�g��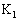 �ɋC�̂������d����
�ɋC�̂������d����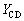 �Ƃ����B
�Ƃ����B ��8�@���u�̏�Ԃ��T�C�N��A��B��C��D��A�ɏ]���ĕω�������Ƃ��A���u�S�̂��O�ɂ����d��W���A���u���������̂�����M��Q�Ŋ������ʂ��A���̃T�C�N���̌����ƌĂԁB��6�C��7�̌��ʂ𗘗p���A���������߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�v�X�Ɍ��������̓��ł��B�C�̂��ړ����Ă��܂��̂ŁA���u�S�̂Ƃ���pV�}��`���Ďd�����l���邱�Ƃ��ł��܂���B��7�̈Ӗ��s���̃q���g���牽��ǂݎ�邩�A�Ƃ������Ƃ�����Ă��܂��B�Đ���G���ӎ������A�e�� ����Ή��x
����Ή��x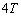 �ɂȂ����C�̂��e��
�ɂȂ����C�̂��e�� �Ɉړ����A�e��
�Ɉړ����A�e��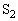 ����Ή��xT�ɂȂ����C�̂��e��
����Ή��xT�ɂȂ����C�̂��e��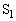 �Ɉړ�����A�ƁA�l���܂��傤�B
�Ɉړ�����A�ƁA�l���܂��傤�B
�e��1�C�e��2�̋C�̂̃�������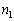 �C
�C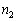 �C�e��1�C�e��2�̋C�̂��̐���
�C�e��1�C�e��2�̋C�̂��̐���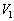 �C
�C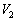 �Ƃ��܂��B
�Ƃ��܂��B
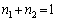 �@����@
�@����@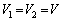 )�C���D�ɂ����ẮA
)�C���D�ɂ����ẮA �@����A
�@����A
���B�C���D�ɂ����ẮA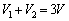 �@����B
�@����B
�ȉ��A���A�CB�CC�CD�ɂ����āA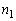 �C
�C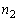 �C
�C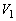 �C
�C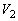 �̒l���ω����邱�Ƃɒ��ӂ��Ă��������B
�̒l���ω����邱�Ƃɒ��ӂ��Ă��������B
��1�@���A�ɂ����āA
�e��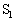 ����ԕ������F
����ԕ������F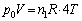 �@����C
�@����C
�e��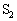 ����ԕ������F
����ԕ������F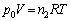 �@����D
�@����D
�C���D���A
�@���A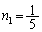 �C
�C
�D�ɑ������ƁA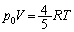
�� 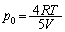 ......[��]
......[��]
��2�@���B�ɂ����āA
�e��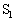 ����ԕ������F
����ԕ������F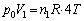 �@����E
�@����E
�e�� ����ԕ������F
����ԕ������F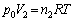 �@����F
�@����F
�F���E���A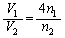
�B���A
�� 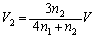 �C
�C �@����G
�@����G
�F�ɑ�����āA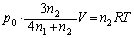
��1�̌��ʂ��A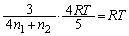
�� 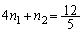 ����Ƈ@��A�����āA
����Ƈ@��A�����āA 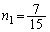 �C
�C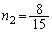
�G�ɑ�����āA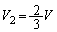 �C
�C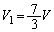 ......[��]
......[��]
��3�@���B�Ə��C�̈Ⴂ�́A������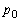 ���������̂�
���������̂�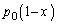 �ɕς�������ƂŁA�G���͏��C�ɂ����Ă��������܂��B
�ɕς�������ƂŁA�G���͏��C�ɂ����Ă��������܂��B �e��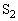 ����ԕ������F
����ԕ������F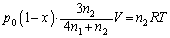
��1�̌��ʂ��A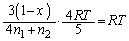
�� 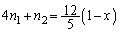 ����Ƈ@��A�����āA
����Ƈ@��A�����āA  �C
�C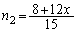
�G�ɑ�����āA
�B���A
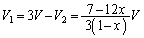 ......[��]
......[��]
��4�@A��B�ɂ����āA���u���̋C�̂��̐ϕω��́A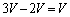
��1�̌��ʂ�p���āA
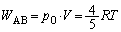 ......[��]
......[��]�e�� ���̋C�̂��̐ϕω��́A
���̋C�̂��̐ϕω��́A �� 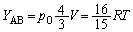 ......[��]
......[��]
��5�@B��C�ɂ����āA���u�S�̂ł���ϕω��Ȃ̂ŁA�C�̂͊O���ɑ����d���������A 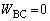 ......[��]
......[��]�e��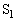 ���̋C�̂��̐ϕω��́A
���̋C�̂��̐ϕω��́A ��  ......[��]
......[��]
��6�@���D�ɂ����āA
�e�� ����ԕ������F
����ԕ������F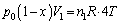 �@����H
�@����H
�e�� ����ԕ������F
����ԕ������F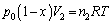 �@����I
�@����I
�H���I���A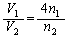
�A���A
��  �C
�C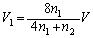 �@����J
�@����J
�I�ɑ�����A
��1�̌��ʂ�p���āA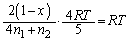
�� 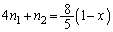 ����Ƈ@��A�����āA
����Ƈ@��A�����āA 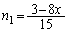 �C
�C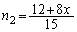
�J�ɑ�����āA
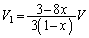 �C
�C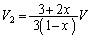
C��D�ɂ����āA�C�̂��̐ϕω��́A
��1�̌��ʂ�p���āA D��A�́A���u�S�̂ł͒�ϕω��ŁA�C�̂̂����d���́A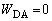
 ......[��]
......[��]C��D�ɂ����āA�e��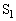 ���̋C�̂��̐ϕω��́A
���̋C�̂��̐ϕω��́A �s�X�g��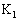 �ɋC�̂������d���́A
�ɋC�̂������d���́A D��A�ɂ����āA�e�� ���̋C�̂��̐ϕω��́A
���̋C�̂��̐ϕω��́A �s�X�g�� �ɋC�̂������d���́A
�ɋC�̂������d���́A �܂��A
�Ƃ��āA
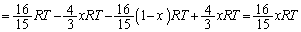 ......[��]
......[��]
��7�@���A�CB�CC�CD�̂�����ɂ����Ă��A�����̔M���͗e��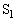 ���̋C�̂��M����o�������Ă��āA�ቷ�̔M���͗e��
���̋C�̂��M����o�������Ă��āA�ቷ�̔M���͗e�� ���̋C�̂����M���D�������Ă��邱�Ƃɒ��ӂ��܂��B��蕶�̃q���g�́A�M�̈ړ����e��
���̋C�̂����M���D�������Ă��邱�Ƃɒ��ӂ��܂��B��蕶�̃q���g�́A�M�̈ړ����e��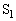 ����e��
����e��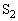 �ւ̋C�̂̈ړ��ɔ����ċN���邱�Ƃ��w�E���Ă���ƍl���Ă��������B
�ւ̋C�̂̈ړ��ɔ����ċN���邱�Ƃ��w�E���Ă���ƍl���Ă��������B �e��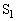 ���M�͊w���@�����l����ƁA���A����n�܂��ď��A�ɖ߂��Ă���̂ŁA1�T�C�N���ł������G�l���M�[�̕ω���0�ł��B1�T�C�N���ŗe��1�����C�̂������d���͖�6��Y�ł��B����āA�M�͊w���@�����A���u�������̔M���������M��Q�́A
���M�͊w���@�����l����ƁA���A����n�܂��ď��A�ɖ߂��Ă���̂ŁA1�T�C�N���ł������G�l���M�[�̕ω���0�ł��B1�T�C�N���ŗe��1�����C�̂������d���͖�6��Y�ł��B����āA�M�͊w���@�����A���u�������̔M���������M��Q�́A 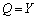 ......[��]
......[��]
��8�@���u������η�́A�C�̂��O���ɂ����d���������M�������������M�Ŋ����āA 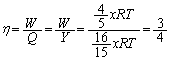 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 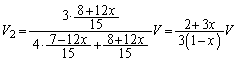
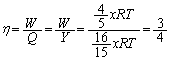 ......[��]
......[��]