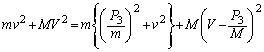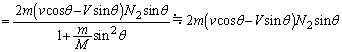���嗝�H����'09�N[3]
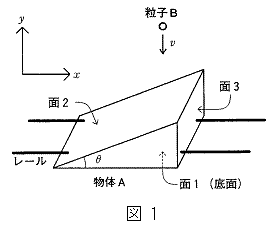 ��ԂɌŒ肳�ꂽ�����ɒ���2�{�̃��[��������B���[����x���ɕ��s�ł���B���̃��[���ɂ����ĉ^�����鎿��M�̕���A���l����(�}1)�B����A��5�̂Ȃ߂炩�Ȗʂ����B��1��2�ӂ����[���ɕ��s�Ȓ����`�ŁA���Ay���ɐ����ł���B��2�͖�1�Ƃ̂Ȃ��p��θ �̎Ζʂł���B��3��x���ɐ����ł���B�c���2�̖ʂ͂��ꂼ���1�ɐ����ł���B
��ԂɌŒ肳�ꂽ�����ɒ���2�{�̃��[��������B���[����x���ɕ��s�ł���B���̃��[���ɂ����ĉ^�����鎿��M�̕���A���l����(�}1)�B����A��5�̂Ȃ߂炩�Ȗʂ����B��1��2�ӂ����[���ɕ��s�Ȓ����`�ŁA���Ay���ɐ����ł���B��2�͖�1�Ƃ̂Ȃ��p��θ �̎Ζʂł���B��3��x���ɐ����ł���B�c���2�̖ʂ͂��ꂼ���1�ɐ����ł���B
y���̕��̕����Ɉ��̑���v�ʼn^�����鎿��m�̗��qB������A�ɏՓ˂���B�Փ˂͒e���Փ˂Ƃ���B���qB�ƕ���A�Ƃ̊Ԃ̖��C�A����яd�͖͂�������B���̂Ƃ��A�ȉ��̖₢�ɓ�����B
�܂��A����A�����[���ɌŒ肳�ꂽ���l����B
��1�@���qB������A�̖�2�ɏՓ˂���Ƃ��A���qB�͖�2�ɐ����ȗ͐ς���B�͐ς̑傫����P�Ƃ��A���qB�̏Փˌ�̑��x��x������y���������ꂼ�� �C
�C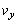 �Ƃ��āA
�Ƃ��āA ��P�̊W���A�����
��P�̊W���A����� ��P�̊W�������ꂼ�ꏑ���B
��P�̊W�������ꂼ�ꏑ���B ��2�@�Փ˂̑O��ŗ��qB�̉^���G�l���M�[���ۑ�����邱�Ƃ�p���āAP�����߂�B����v�Cm�Cθ �̂����K���Ȃ��̂�p���ĕ\���B
���ɁA����A�����[���ɂ����Ď��R�ɓ�������l����B���[���ƕ���A�Ƃ̊Ԃ̖��C�͖�������B
��3�@����V��x���̐��̕����ɓ����Ă��镨��A�̖�2�ɗ��qB���Փ˂���Ƃ��A��1�Ɠ��l�ɁA���qB�͖�2�ɐ����ȗ͐ς���B���̂Ƃ��A���qB����͐ς̑傫��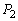 �����߂�B����v�CV�Cm�CM�Cθ �̂����K���Ȃ��̂�p���ĕ\���B
�����߂�B����v�CV�Cm�CM�Cθ �̂����K���Ȃ��̂�p���ĕ\���B ��4�@����V��x���̐��̕����ɓ����Ă��镨��A�̖�3�ɗ��qB���Փ˂���Ƃ��A���qB�͖�3�ɐ����ȗ͐ς���B���̗͐ς̑傫��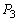 �����߂�B����v�CV�Cm�CM�Cθ �̂����K���Ȃ��̂�p���ĕ\���B
�����߂�B����v�CV�Cm�CM�Cθ �̂����K���Ȃ��̂�p���ĕ\���B  ����ɁA���qB�Ɠ������q����ԂɈ�l�ɕ��z���Ă���A���ꂼ�ꂪy���̕��̕����Ɉ��̑���v�ʼn^�����A����A�ƏՓ˂�����l����(�}2)�B�P�ʑ̐ς�����̗��q����n�Ƃ���B����A�̎���M�����q�̎���m�����\���ɑ傫���A�����n���\���ɑ傫���Ƃ��A�����̗��q�̏Փ˂ɂ���Đ����镽�ς̗͂ɂ��A����A�͂Ȃ߂炩�ɉ^������B���̂Ƃ��̕���A�̉^���ɂ��čl����B���q�ƕ���A�Ƃ̏Փ˂͂��ׂĒe���Փ˂Ƃ���B���[���ƕ���A�Ƃ̊Ԃ̖��C�A���q�ƕ���A�Ƃ̊Ԃ̖��C�A����яd�͖͂�������B�܂��A���q���m�̏ՓˁA����ї��q�ƃ��[���Ƃ̏Փ˂���������B���̂Ƃ��A�ȉ��̖₢�ɓ�����B
����ɁA���qB�Ɠ������q����ԂɈ�l�ɕ��z���Ă���A���ꂼ�ꂪy���̕��̕����Ɉ��̑���v�ʼn^�����A����A�ƏՓ˂�����l����(�}2)�B�P�ʑ̐ς�����̗��q����n�Ƃ���B����A�̎���M�����q�̎���m�����\���ɑ傫���A�����n���\���ɑ傫���Ƃ��A�����̗��q�̏Փ˂ɂ���Đ����镽�ς̗͂ɂ��A����A�͂Ȃ߂炩�ɉ^������B���̂Ƃ��̕���A�̉^���ɂ��čl����B���q�ƕ���A�Ƃ̏Փ˂͂��ׂĒe���Փ˂Ƃ���B���[���ƕ���A�Ƃ̊Ԃ̖��C�A���q�ƕ���A�Ƃ̊Ԃ̖��C�A����яd�͖͂�������B�܂��A���q���m�̏ՓˁA����ї��q�ƃ��[���Ƃ̏Փ˂���������B���̂Ƃ��A�ȉ��̖₢�ɓ�����B
��5�@����A��x���̐��̕����ɑ���V�œ����Ă���Ƃ��A����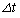 �̊Ԃɗ��q������A�̖�2�ɋy�ڂ����ς̗͂�x������
�̊Ԃɗ��q������A�̖�2�ɋy�ڂ����ς̗͂�x������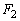 �C��3�ɋy�ڂ����ς̗͂�
�C��3�ɋy�ڂ����ς̗͂�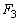 �Ƃ���B����A�̎��ʂ͗��q�̎��ʂ����\���ɑ傫��(
�Ƃ���B����A�̎��ʂ͗��q�̎��ʂ����\���ɑ傫��(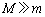 )�A����Ɏ���
)�A����Ɏ���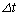 �͏\���ɒZ�����߁A
�͏\���ɒZ�����߁A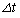 �Ԃ̕���A�̑����͈��Ƃ݂Ȃ���B
�Ԃ̕���A�̑����͈��Ƃ݂Ȃ���B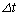 �̊Ԃɕ���A�̖�2�A����і�3�ɏՓ˂��闱�q�̐������ꂼ��
�̊Ԃɕ���A�̖�2�A����і�3�ɏՓ˂��闱�q�̐������ꂼ��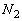 �C
�C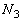 �Ƃ��āA
�Ƃ��āA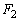 �C
�C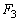 �����ꂼ�ꋁ�߂�B����m�Cv�CV�C
�����ꂼ�ꋁ�߂�B����m�Cv�CV�C �C
�C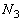 �C
�C �Cθ �̂����K���Ȃ��̂�p���ĕ\���B
�Cθ �̂����K���Ȃ��̂�p���ĕ\���B ��6�@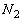 �C
�C �����ꂼ�ꋁ�߂�B�������A��2�̑̐ς�S�Ƃ���B����v�CV�Cn�C
�����ꂼ�ꋁ�߂�B�������A��2�̑̐ς�S�Ƃ���B����v�CV�Cn�C �Cθ�CS�̂����K���Ȃ��̂�p���ĕ\���B
�Cθ�CS�̂����K���Ȃ��̂�p���ĕ\���B ��7�@�\���Ɏ��Ԃ����ƁA����A�͏����x�ɂ�炸��x���̐��̕����ɓ����x�^��������悤�ɂȂ�B����A�̎��ʂ͗��q�̎��ʂ����\���ɑ傫���Ƃ���(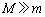 )�A���̂Ƃ��̕���A�̑��������߂�B����v��θ ��p���ĕ\���B
)�A���̂Ƃ��̕���A�̑��������߂�B����v��θ ��p���ĕ\���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�e95�N[1]�ł��o�肳�ꂽ�ΏՓ˂��e�[�}�Ƃ�����ł����A����x�̏�Ƀ{�����[���������Ղ�ŁA�������ԓ��ɉ������邱�Ƃ͖����ł͂Ȃ����Ǝv���܂��B
�������Ƃ��Ă͖�3�܂łŏ[���ŁA��3�ɂ��Ă��A�U�������Ȃ���A�Ɏ��邽�߂ɏ\���ȗ��������邱�Ƃ͍���ł͂Ȃ��ł��傤���B
�Ȃ��A�ՓˁE���́E����̖�����Q�Ƃ��Ă��������B
��1�@���qB�����͐���x������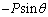 �Cy������
�Cy������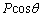 �ł��B�^���ʂ̌������Ax�����ɂ��āA
�ł��B�^���ʂ̌������Ax�����ɂ��āA  ......[��]
......[��]y�����ɂ��āA
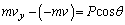 ......[��]
......[��]���D �C
�C �C
�C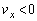 �C
�C �ɒ��ӂ��Ă��������B
�ɒ��ӂ��Ă��������B
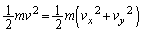 �@����@
�@����@��1�̌��ʂ�p���āA
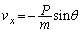 �C
�C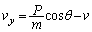
�������@�ɑ�����A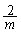 �������āA
�������āA ��  ���qB�͖�2�ɐ������͐�����̂�
���qB�͖�2�ɐ������͐�����̂� �C����āA
�C����āA 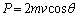 ......[��]
......[��]
��3�@�Փˌ�̗��qB�����x�̑傫����u�C��2�ɐ����ȕ����ƂȂ��p��φ�Ƃ���ƁA�Ζʂɉ��������ɂ��͐����Ȃ��̂ŁA���qB�����x�̎Ζʂɉ��������̐����͏ՓˑO��ŕω������A
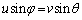 �@����A
�@����A���qB�͖�2�ɐ������͐�(�傫��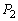 )����̂ŁA��2�ɐ����ȕ����ɂ��āA�^�����̌������A
)����̂ŁA��2�ɐ����ȕ����ɂ��āA�^�����̌������A 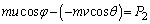 �@����B
�@����B���qB����2�ɐ����ő傫��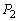 ���͐�����Ƃ������Ƃ́A����A�͂���Ɠ���t�������͐�����Ƃ������Ƃł�(��p����p�̖@�����Q��)�B����A�����͐��́A���qB�����͐��̔���p�̐��������ɓ������A�傫����
���͐�����Ƃ������Ƃ́A����A�͂���Ɠ���t�������͐�����Ƃ������Ƃł�(��p����p�̖@�����Q��)�B����A�����͐��́A���qB�����͐��̔���p�̐��������ɓ������A�傫���� �C������x���������ł��B����A�Ɋւ��āAx���������^���ʂ̌������A
�C������x���������ł��B����A�Ɋւ��āAx���������^���ʂ̌������A  �@����C
�@����C�Փˎ��_�Ōn���d���������O���͑��݂����A�ՓˑO��̌n���^���G�l���M�[�͕ۑ�����A
 �@����D
�@����D�A�C�B���A
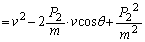 �@����E
�@����E�C���A
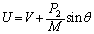 �@����F
�@����F�E�C�F���D�ɑ������2�{����ƁA
�������āA
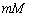 �������āA
�������āA���qB�͖�2�ɐ������͐�����̂�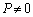 �C����āA
�C����āA 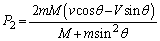 ......[��]
......[��]���D�C�͌n��x���������^���ʕۑ����Ӗ����܂����Ay�������ł́A���[��������A�ɋy�ڂ������R���������̂ŁA�n���^�����͕ۑ����Ȃ����Ƃɒ��ӂ��Ă��������B
��4�@�Փˌ�̗��qB��������u�C���qB�����x��x���������ƂȂ��p��φ�Ƃ���ƁA����x������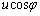 �Cy������
�Cy������ �ł��B
�ł��B ���qB�͖�3�ɐ����ȕ����ɑ傫�� ���͐�����̂ŁAx���������^���ʂ̌����ɂ��A
���͐�����̂ŁAx���������^���ʂ̌����ɂ��A 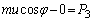 �@����G
�@����G���qB��y�������ɂ��͐����Ȃ��̂ŁA���qB�����x��y�����������͕ω������A
 �@����H
�@����H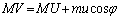 �@����I
�@����I�Փˎ��_�Ōn���d���������O���͑��݂����A�ՓˑO��̌n���^���G�l���M�[�͕ۑ�����A
 �@����J
�@����J�G�C�H���A
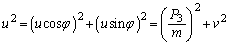 �@����K
�@����K�G�C�I���A
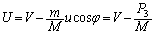 �@����L
�@����L�K�C�L���J�ɑ������2�{����ƁA
�������āA
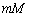 �������āA
�������āA���qB�͖�2�ɐ������͐�����̂�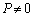 �C����āA
�C����āA 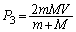 ......[��]
......[��]
��5�@��3�C��4��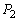 �C
�C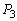 �͗��q1����2������͐��̑傫���ŁA����A�͗��q1���炱��̔���p�ƂȂ��͐����܂��B��2�A��3�ɏՓ˂��闱�q��
�͗��q1����2������͐��̑傫���ŁA����A�͗��q1���炱��̔���p�ƂȂ��͐����܂��B��2�A��3�ɏՓ˂��闱�q�� �A
�A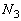 ����ꍇ�ɂ́A����A�̖�2�C��3�����͐��̑傫����
����ꍇ�ɂ́A����A�̖�2�C��3�����͐��̑傫����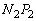 �C
�C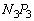 �ƂȂ�܂��B
�ƂȂ�܂��B ����āA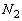 �̗��q����2�ɋy�ڂ����ς�����x������
�̗��q����2�ɋy�ڂ����ς�����x������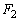 �Ƃ��āA
�Ƃ��āA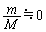 �Ƃ���ƁA
�Ƃ���ƁA �� 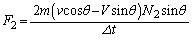 ......[��]���l�ɁA
......[��]���l�ɁA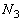 �̗��q����3�ɋy�ڂ����ς���
�̗��q����3�ɋy�ڂ����ς���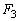 �́A
�́A �� 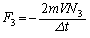 ......[��]�@(
......[��]�@(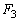 �̌�����x��������)
�̌�����x��������)
 ��6�@��蕶�̐��������X����܂��A�����͖�5�̌��ʂ�p����
��6�@��蕶�̐��������X����܂��A�����͖�5�̌��ʂ�p����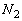 �C
�C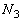 �����߂�̂ł͂Ȃ��A��7�̂��߂ɁA��5��
�����߂�̂ł͂Ȃ��A��7�̂��߂ɁA��5�� �C
�C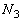 �𗱎q�̖��xn��p���ĕ\�����Ƃ��ڕW�ł��B
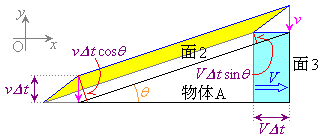
�𗱎q�̖��xn��p���ĕ\�����Ƃ��ڕW�ł��B����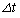 �̊Ԃɕ���A��x��������
�̊Ԃɕ���A��x��������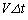 �ړ�����̂ŁA��2�ɏՓ˂��闱�q�̌�
�ړ�����̂ŁA��2�ɏՓ˂��闱�q�̌�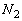 �͉E�}�̉��F���F�����ɑ��݂��闱�q�̌��ł��B���̕������̐��́A��ʐ�S�ŁA�������E�}���
�͉E�}�̉��F���F�����ɑ��݂��闱�q�̌��ł��B���̕������̐��́A��ʐ�S�ŁA�������E�}���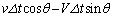 �Ȃ̂ŁA
�Ȃ̂ŁA �ł��B����āA
�ł��B����āA 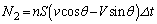 ......[��]
......[��]��3�ɏՓ˂��闱�q�̌�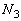 �͉E�}�̐��F���F�����ɑ��݂��闱�q�̌��ł��B���̕������̐��́A
�͉E�}�̐��F���F�����ɑ��݂��闱�q�̌��ł��B���̕������̐��́A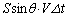 �ł��B����āA
�ł��B����āA 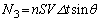 ......[��]
......[��]
��7�@����A�������x�^��������Ƃ��A����A�ɐ��������ɓ����͂̂肠�����A ��5�C��6�̌��ʂ��A
 �C
�C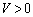 ���A
���A��  ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B