力学(円運動・単振動)演習問題(その2)
立命館大物理'08年[3]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
次の文章の あ 〜 け に適切な数式を記せ。 ア 〜 ウ には選択肢より適切な番号を選べ。
水平面上に置かれ、一定の角速度 で回転する半径
で回転する半径 の円板を考える。円板上にはレールが敷かれている。レールの上には質量
の円板を考える。円板上にはレールが敷かれている。レールの上には質量 の小球があり、レールの上を移動することができる。このとき、以下の問いに答えよ。
の小球があり、レールの上を移動することができる。このとき、以下の問いに答えよ。
 [1] 図−aのようにレールが直径AB上に設置され、小球は、円板の中心Oに固定された支柱と、自然長
[1] 図−aのようにレールが直径AB上に設置され、小球は、円板の中心Oに固定された支柱と、自然長 ,バネ定数
,バネ定数 のバネで結合されている。円板とともに回転している観測者から見て小球が静止しているとき、小球から中心Oまでの距離が
のバネで結合されている。円板とともに回転している観測者から見て小球が静止しているとき、小球から中心Oまでの距離が であった。
であった。小球に働く遠心力の大きさは あ  である。摩擦が無視できるとき、バネの弾性力とのつり合いから距離
である。摩擦が無視できるとき、バネの弾性力とのつり合いから距離 は
は

となる。さらに、小球が円板上にとどまるためには、バネ定数kは

でなければならない。
 [2] 図−bのようにレールが弦CE上に設置され、小球は、弦CEの中点Dに固定された支柱と、先と同等に自然長
[2] 図−bのようにレールが弦CE上に設置され、小球は、弦CEの中点Dに固定された支柱と、先と同等に自然長 ,バネ定数kのバネで結合されている。弦CEの中心角
,バネ定数kのバネで結合されている。弦CEの中心角 は
は である。円板とともに回転している観測者から見て小球が静止しているとき、小球から中点Dまでの距離が
である。円板とともに回転している観測者から見て小球が静止しているとき、小球から中点Dまでの距離が であった。
であった。小球と円板(レール底面)との摩擦は無視できるが、小球とレール壁面の摩擦は無視できず、その静止摩擦係数がμであるとする。小球に働くレール方向の遠心力の大きさは お  である。レール壁面から横方向に小球が受ける垂直抗力の大きさは か
である。レール壁面から横方向に小球が受ける垂直抗力の大きさは か  であるので、レール方向の最大(静止)摩擦力の大きさ
であるので、レール方向の最大(静止)摩擦力の大きさ は、
は、 き である。
き である。
このとき、小球が円板上で静止状態を保ち、動き出さないための距離 の上限は、
の上限は、

である。ただしバネ定数kは十分大きく、小球は常にCD上にとどまるとする。
ここで、図−a,図−bの円板からそれぞれバネと支柱を取り除き、図− ,図−
,図− のように小球がレール上を移動することができるようにした。
のように小球がレール上を移動することができるようにした。
 [3] ニュートンの運動の第一法則は、次のように表現される。
[3] ニュートンの運動の第一法則は、次のように表現される。物体が外部から力を受けないか、あるいは外部から受ける力の合力がゼロである場合、静止している物体はいつまでも静止し続け、運動している物体は等速直線運動を続ける。
これを慣性の法則という。例えば、図− ,図−
,図− においては、回転する円板上でなく円板の外で静止している観測者から見たときに慣性の法則が成立することに注意しよう。
においては、回転する円板上でなく円板の外で静止している観測者から見たときに慣性の法則が成立することに注意しよう。
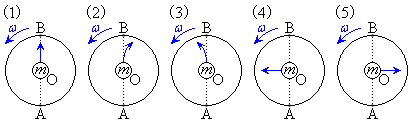
さて、図− において、小球が点Aから点Bに向かって直径上のレールを滑る。小球が中心Oを通過した瞬間にレールを取り払い、小球が円板上を摩擦なく自由に運動できるようにした。その後の小球は、円板の外で静止している観測者の視点では慣性の法則に従って運動を続ける。この運動を中心Oで円板とともに回転している観測者から見ると、 ア のような運動として観測される。
において、小球が点Aから点Bに向かって直径上のレールを滑る。小球が中心Oを通過した瞬間にレールを取り払い、小球が円板上を摩擦なく自由に運動できるようにした。その後の小球は、円板の外で静止している観測者の視点では慣性の法則に従って運動を続ける。この運動を中心Oで円板とともに回転している観測者から見ると、 ア のような運動として観測される。
 [4] 図−
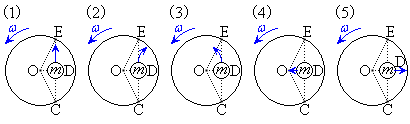
[4] 図− において、小球が点Cから点Eに向かって弦CE上のレールを滑る。小球が中点Dを通過した瞬間にレールを取り払い、小球が円板上を摩擦なく自由に運動できるようにした。この運動を中心Oで円板とともに回転している観測者から見ると、 イ のような運動として観測される。
において、小球が点Cから点Eに向かって弦CE上のレールを滑る。小球が中点Dを通過した瞬間にレールを取り払い、小球が円板上を摩擦なく自由に運動できるようにした。この運動を中心Oで円板とともに回転している観測者から見ると、 イ のような運動として観測される。
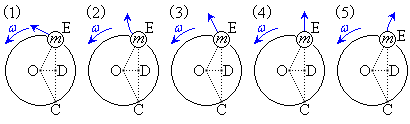
[5] 図− において、小球が点Cから点Eまで弦CE上のレールを滑る。点Eを通過した後、小球はそのままレールから飛び出した。その後の小球は、円板の外で静止している観測者から見ると、 ウ のような運動を行う。ただし、円板上面と水平面の段差は無視できるとする。
において、小球が点Cから点Eまで弦CE上のレールを滑る。点Eを通過した後、小球はそのままレールから飛び出した。その後の小球は、円板の外で静止している観測者から見ると、 ウ のような運動を行う。ただし、円板上面と水平面の段差は無視できるとする。 ア の選択肢
イ の選択肢
ウ の選択肢
[解答へ]
関西学院大物理'08年[1]
 図のように半径Rの半円部ABC,半径Rの半円部DEF,長さ
図のように半径Rの半円部ABC,半径Rの半円部DEF,長さ の直線部CDからなる絶縁体の細いレールが水平な床上に設置されている。レールはひとつの鉛直面(xy平面、x軸は水平方向、y軸は鉛直方向)内にあり、直線部CDはx軸に平行である。物体1の質量はm,物体2の質量は
の直線部CDからなる絶縁体の細いレールが水平な床上に設置されている。レールはひとつの鉛直面(xy平面、x軸は水平方向、y軸は鉛直方向)内にあり、直線部CDはx軸に平行である。物体1の質量はm,物体2の質量は である。物体2は正に帯電しており、半円部DEFの中心点Gには物体2の電荷と同じ大きさの負電荷が固定されている。重力加速度の大きさをg,静電気力に関するクーロンの法則の比例定数をkとして、以下の問(1)〜(5)に答えよ。なお物体1と物体2の大きさや、レールと物体1,レールと物体2との摩擦、および空気抵抗は無視できるものとする。
である。物体2は正に帯電しており、半円部DEFの中心点Gには物体2の電荷と同じ大きさの負電荷が固定されている。重力加速度の大きさをg,静電気力に関するクーロンの法則の比例定数をkとして、以下の問(1)〜(5)に答えよ。なお物体1と物体2の大きさや、レールと物体1,レールと物体2との摩擦、および空気抵抗は無視できるものとする。
(1) 点Aで物体1に水平右向き(x軸の正方向)の初速度を与えると、その速さが十分に大きい場合には、物体1はレールの半円部ABCの内周側をレールから離れることなく、A→B→Cと移動できるが、速さが小さい場合には物体1は半円部ABCから離れて落下する。
(a) 物体1がレールの半円部ABCから離れずに点Cまで到達できる、点Aにおける最小の初速度の大きさを求めよ。
以下では物体1は、問(a)で求めた初速度で点Aよりレールに沿って運動を開始する。
(b) 物体1がレールから受ける垂直抗力の大きさを、レールに沿った点Aからの距離の関数として点Aから点Dまでの範囲について求め、グラフに表せ。
物体1は点Dで静止していた物体2に衝突する。この衝突は完全弾性衝突であり、物体1と物体2の間での電荷の移動や物体2の電気量の増減は生じないものとする。
(2) 衝突直度の物体1と物体2の速さは、それぞれいくらになるか。
(3) 衝突後の物体1が、最初に床に達した地点を点Hとする。HF間の距離はいくらになるか。
(4) 物体2がレールから離れることなく、半円部DEFの外周部を移動し、点Fに達するために必要な電気量の大きさの最小値を求めよ。
(5) 点Fに達する直前の物体2の運動エネルギーと、点Hに達する直前の物体1の運動エネルギーの総和は、物体1が点Cを通過した瞬間にもっていた運動エネルギーからどれくらい変化しているか。 [解答へ]
九大物理'09年[3]
文中の空欄 ア から ソ にあてはまる数式を答えよ。ただし、角度および角速度の単位は、それぞれradおよびrad/sとし、円周率はπとする。必要があれば、三角関数の公式
を用いてよい。また、θ の大きさが十分小さいときには、 ,
, とせよ。
とせよ。
 問1 図4のように、xy平面上で時計回りに角速度の大きさがω で等速円運動をする物体を考える。xy座標の原点を円の中心とし、時刻tでの物体の位置
問1 図4のように、xy平面上で時計回りに角速度の大きさがω で等速円運動をする物体を考える。xy座標の原点を円の中心とし、時刻tでの物体の位置 を
を と表す。ただし、円の半径をrとし、時刻0では
と表す。ただし、円の半径をrとし、時刻0では とする。同様に、速度
とする。同様に、速度 を
を ,加速度
,加速度 を
を と表す。答えは、r,ω,tの中から必要な記号を用いて表せ。
と表す。答えは、r,ω,tの中から必要な記号を用いて表せ。時刻tでの物体の位置については、 ア ,
ア , イ である。時刻0から
イ である。時刻0から までの位置の変化
までの位置の変化 は、
は、 が十分小さいときには
が十分小さいときには に等しいので、
に等しいので、 ウ ,
ウ , エ である。
エ である。 と
と のなす角は
のなす角は であるから、
であるから、 オ ,
オ , カ となる。同様に、速度の変化
カ となる。同様に、速度の変化 は
は に等しいので、
に等しいので、 キ ,
キ , ク である。
ク である。 と
と のなす角は
のなす角は であるから、
であるから、 ケ ,
ケ , コ となる。
コ となる。  問2 図5のように、質量mの多数の物体を、質量が無視できるバネ定数kの同じバネでつなぎ、なめらかな水平面上の直線(x軸)に沿って静止させる。このとき、各物体の間隔はdであり、左端からn番目の物体の位置
問2 図5のように、質量mの多数の物体を、質量が無視できるバネ定数kの同じバネでつなぎ、なめらかな水平面上の直線(x軸)に沿って静止させる。このとき、各物体の間隔はdであり、左端からn番目の物体の位置 を
を とする。次に、それぞれの物体を振幅r,角振動数ω でx方向に単振動させる。時刻tにおいて、n番目の物体がはじめに静止していた位置
とする。次に、それぞれの物体を振幅r,角振動数ω でx方向に単振動させる。時刻tにおいて、n番目の物体がはじめに静止していた位置 からの変位を
からの変位を とする。以下では、すべての物体の変位が図6に示すように波長λの正弦波上にあり、時間の経過にしたがって、この正弦波がx軸の正の向きに進む場合を考える。このとき、λはdにくらべて十分に大きく、物体に作用する力はバネによるもののみとする。 答えは、r,ω,t,d,λ,m,kの中から必要な記号を用いて表せ。
とする。以下では、すべての物体の変位が図6に示すように波長λの正弦波上にあり、時間の経過にしたがって、この正弦波がx軸の正の向きに進む場合を考える。このとき、λはdにくらべて十分に大きく、物体に作用する力はバネによるもののみとする。 答えは、r,ω,t,d,λ,m,kの中から必要な記号を用いて表せ。
[解答へ]
横浜国大物理'09年[1]
 図のように、水平からの角度θ のなめらかで摩擦のない斜面上にばね定数
図のように、水平からの角度θ のなめらかで摩擦のない斜面上にばね定数 のばねがあり、その一端が斜面上の壁に固定されている。ばねの他端に質量
のばねがあり、その一端が斜面上の壁に固定されている。ばねの他端に質量 の板が取り付けられ、つりあいの状態にある。ここで、この板のつりあいの位置を基準とした高さ
の板が取り付けられ、つりあいの状態にある。ここで、この板のつりあいの位置を基準とした高さ の斜面上の位置に質量
の斜面上の位置に質量 の小球を置いて静かに手を離すと、小球は運動を始め、板に衝突した。小球と板の大きさ、および、ばねの質量は無視できるものとする。また、重力加速度を
の小球を置いて静かに手を離すと、小球は運動を始め、板に衝突した。小球と板の大きさ、および、ばねの質量は無視できるものとする。また、重力加速度を とする。以下の文章の空欄を埋めよ。
とする。以下の文章の空欄を埋めよ。
手を離してから小球が板に衝突するまでの時間は、 (1) [s]であり、衝突直前の小球の速さは (2) [m/s]である。
小球と板は完全非弾性衝突をし、衝突後一体となって運動した。ただし、衝突中の外力による力積は無視できるものとする。衝突直後の小球と板の速さは (3) [m/s]である。また、衝突によって失われた小球と板の力学的エネルギーは (4) [J]となる。
一体となった小球と板は、斜面上の壁の手前のある位置で折り返す単振動をした。この単振動の中心は、ばねが自然長から (5) [m]だけ縮んだ位置であり、周期は (6) [s]である。小球が板に衝突した直後から、
(6) [s]である。小球が板に衝突した直後から、 後の小球と板の位置は、ばねが自然長から (7) [m]だけ縮んだときの位置となる。
後の小球と板の位置は、ばねが自然長から (7) [m]だけ縮んだときの位置となる。
以下では、小球と板の最高点がばねの自然長での位置と一致するような単振動をした場合を考える(これ以降は記号hを使用せずに解答すること)。このとき、小球の初期の高さhは (8) [m]と表せる。また、単振動中の小球と板の最大の速さは (9) [m/s]である。小球が板に衝突した直後から小球と板が最初に最高点に達するまでに、ばねの弾性力が小球と板にした仕事は (10) [J],重力が小球と板にした仕事は (11) [J]である。
[解答へ]
東北大物理'10年前期[1]
 図1のように、半径Rの円柱を4分の1にした台(以下、曲面台とよぶ)を水平な床面に置き、その曲面台の上方に左端が固定されたばねをのせた台を水平に配置する(以下、水平台とよぶ)。ばねの右端部には互いに連結された質量
図1のように、半径Rの円柱を4分の1にした台(以下、曲面台とよぶ)を水平な床面に置き、その曲面台の上方に左端が固定されたばねをのせた台を水平に配置する(以下、水平台とよぶ)。ばねの右端部には互いに連結された質量 の小球Aと質量mの小球Bが取り付けてある。曲面台の最上部Sから水平台上面までの高さhは、水平台を水平のまま上下させることで変えることができる。重力加速度をg,ばね定数をk,曲面台と小球のはねかえり係数を1 (弾性衝突)とする。また、小球A,Bの大きさ、水平台の厚み、摩擦、空気抵抗の影響は無視でき、小球A,Bは紙面内でのみ運動し、曲面台は床面に固定されているものとして以下の問いに答えよ。解答は解答用紙の所定の場所に記入せよ。また、結果だけでなく、考え方や計算の過程も記せ。
の小球Aと質量mの小球Bが取り付けてある。曲面台の最上部Sから水平台上面までの高さhは、水平台を水平のまま上下させることで変えることができる。重力加速度をg,ばね定数をk,曲面台と小球のはねかえり係数を1 (弾性衝突)とする。また、小球A,Bの大きさ、水平台の厚み、摩擦、空気抵抗の影響は無視でき、小球A,Bは紙面内でのみ運動し、曲面台は床面に固定されているものとして以下の問いに答えよ。解答は解答用紙の所定の場所に記入せよ。また、結果だけでなく、考え方や計算の過程も記せ。
問(1) ばねを自然長からdだけ縮めてから手を離すと単振動を起こした。最初、小球A,B間は互いに連結されているが、何周期か振動した後、小球が右方向に運動していて、ばねがちょうど自然長となったとき、小球A,Bの間の連結を切り離した。
(a) 切り離す前の周期 と切り離した後の周期
と切り離した後の周期 の比
の比 を求めよ。
を求めよ。 (b) 切り離した直後の小球Bの速度vを、m,g,k,dの中から必要なものを用いて表せ。
(c) 切り離した後の小球Aの振幅 を、m,g,k,dの中から必要なものを用いて表せ。
を、m,g,k,dの中から必要なものを用いて表せ。
問(2) 切り離された小球Bは、水平台上を移動した後、水平台の右端から速度 で飛び出した。その後、図1のように
で飛び出した。その後、図1のように となる曲面台表面の点Pに衝突し、さらに、はねかえって床面上に落下した。このとき、
となる曲面台表面の点Pに衝突し、さらに、はねかえって床面上に落下した。このとき、 とし、小球Bは点Pで曲面台の表面に接するなめらかな平面ではねかえるとみなせることとする。
とし、小球Bは点Pで曲面台の表面に接するなめらかな平面ではねかえるとみなせることとする。 (a) 点Pに衝突するために必要な速度 を、m,g,Rの中から必要なものを用いて表せ。
を、m,g,Rの中から必要なものを用いて表せ。 (b) 点Pで、はねかえり直後における小球Bの速度のx成分とy成分を、m,g,R, の中から必要なものを用いて表せ。ただし、水平右向きをx軸の正の向き、鉛直下方をy軸の正の向きとする。
の中から必要なものを用いて表せ。ただし、水平右向きをx軸の正の向き、鉛直下方をy軸の正の向きとする。
 問(3)
問(3)  のとき、図2のように、小球Bは水平台表面から速度vで曲面台に到達し、さらに曲面台表面上を移動した後、ある点Dで曲面台表面から離れた。このとき、点Dの床面からの高さをHとし、水平台表面と曲面台表面はなめらかにつながっているものとする。
のとき、図2のように、小球Bは水平台表面から速度vで曲面台に到達し、さらに曲面台表面上を移動した後、ある点Dで曲面台表面から離れた。このとき、点Dの床面からの高さをHとし、水平台表面と曲面台表面はなめらかにつながっているものとする。(a) 図2のように をαとしたとき、
をαとしたとき、 をg,R,m,vの中から必要なものを用いて表せ。
をg,R,m,vの中から必要なものを用いて表せ。 (b)  の場合、すなわち曲面台の頂点Sで、小球Bがすぐに曲面台から離れる速度の最小値
の場合、すなわち曲面台の頂点Sで、小球Bがすぐに曲面台から離れる速度の最小値 を、g,R,mを用いて表せ。
を、g,R,mを用いて表せ。 (c) 点Dの高さHと速度vの関係を解答用紙のグラフに実線で描け。ただし、vが問(3)(b)の よりも大きいときと小さいときの両方の場合について示せ。また、vが限りなく0に近いときと
よりも大きいときと小さいときの両方の場合について示せ。また、vが限りなく0に近いときと のときのHの値をグラフの縦軸上に記せ。
のときのHの値をグラフの縦軸上に記せ。 [解答へ]
東北大物理'10年後期[1]
 図1のように、傾きθ の斜面をもつ質量
図1のように、傾きθ の斜面をもつ質量 の台が水平面の溝に置かれている。この斜面上の点Pから質量mの小球を長さ
の台が水平面の溝に置かれている。この斜面上の点Pから質量mの小球を長さ の糸でつるしたところ、点Aの位置で静止した。座標軸は、図のように、水平面と台の斜面が交わった直線に平行な方向にx軸を、溝に平行な方向にy軸を、xy平面に垂直な方向にz軸をとる。小球に、x軸の正の向きに初速度
の糸でつるしたところ、点Aの位置で静止した。座標軸は、図のように、水平面と台の斜面が交わった直線に平行な方向にx軸を、溝に平行な方向にy軸を、xy平面に垂直な方向にz軸をとる。小球に、x軸の正の向きに初速度 を与えたときの運動を考える。重力加速度をgとし、小球の大きさ、糸の質量、すべての摩擦および空気抵抗は無視でき、また、糸は伸び縮みしないものとして以下の問いに答えよ。解答は解答用紙の所定の場所に記入せよ。また、結果だけでなく、考え方や計算の過程も記せ。
を与えたときの運動を考える。重力加速度をgとし、小球の大きさ、糸の質量、すべての摩擦および空気抵抗は無視でき、また、糸は伸び縮みしないものとして以下の問いに答えよ。解答は解答用紙の所定の場所に記入せよ。また、結果だけでなく、考え方や計算の過程も記せ。
問(1) はじめに、台が溝に固定されている場合を考える。初速度を与えた後、小球は斜面上を円運動し、糸がたるむことはなかった。
(a) 小球が図1の点B ( )に達したときの小球の速さ
)に達したときの小球の速さ を、
を、 ,
, ,g,θ を用いて表せ。
,g,θ を用いて表せ。 (b) 小球が最上点Cまで到達するために必要な の最小値を、
の最小値を、 ,g,θ を用いて表せ。
,g,θ を用いて表せ。
問(2) 次に、台が溝の中をy方向にのみ、なめらかに動ける場合を考える。初速度を与えた後、小球は斜面上を円運動し、糸がたるむことはなかった。
(a) 小球の速度のy成分を ,台の速度のy成分をVとする。
,台の速度のy成分をVとする。 とVとの間に成り立つ関係式を記せ。
とVとの間に成り立つ関係式を記せ。  (b) 初速度を与えてから点Cを通過して再び点Aに戻るまでの小球と点Pのy座標の時間変化を、それぞれ太い実線と太い破線として表したグラフとして最も適当なものを、図2の(ア)〜(カ)の中から1つ選び、記号で答えよ。
(b) 初速度を与えてから点Cを通過して再び点Aに戻るまでの小球と点Pのy座標の時間変化を、それぞれ太い実線と太い破線として表したグラフとして最も適当なものを、図2の(ア)〜(カ)の中から1つ選び、記号で答えよ。
問(3)  で、台が溝の中をy方向にのみ、なめらかに動ける場合を考える。小球が最上点Cの位置に到達したときに糸を切った。その後、小球は斜面上を運動して図1の点Dを通過した。ただし、点Dと点Aのz座標は等しいとする。
で、台が溝の中をy方向にのみ、なめらかに動ける場合を考える。小球が最上点Cの位置に到達したときに糸を切った。その後、小球は斜面上を運動して図1の点Dを通過した。ただし、点Dと点Aのz座標は等しいとする。 (a) 小球が点Cの位置に到達したときの台の速度のy成分 を、
を、 ,
, ,gから必要なものを用いて表せ。
,gから必要なものを用いて表せ。 (b) 糸を切った後の台の加速度をaとし、斜面上に固定した座標系から見た点Cから点Aに向かう向きの小球の加速度をbとする。aおよびbの大きさを、gを用いて表せ。台の運動方程式と、斜面上に固定した座標系から見た小球に働く力の斜面に垂直な方向の力のつり合いを考えるとよい。
(c) 小球が点Dに到達したときの台の速度のy成分 を、
を、 ,gを用いて表せ。
,gを用いて表せ。 (d) 小球が点Dに到達したときの小球の速度のy成分およびz成分を、 ,gを用いて表せ。
,gを用いて表せ。 [解答へ]
早大理工物理'11年[2]
 図に示すように、高さを調節できる発射台から水平面上の台車に向けて大きさの無視できる鉄球を水平右方向に打ち出す。台車は、水平で厚みの無視できる上板およびばね定数kのばねから構成されている。上板の質量をMとし、ばねなど台車のそれ以外の部分の質量は無視できるものとする。上板はなめらかで、鉄球に対する反発係数をeとする。ばねと上板は、台車に対して鉛直方向になめらかに運動するものとする。ばねの伸縮が平衡状態のときの上板の位置を鉛直方向の座標原点とし、発射高さはこの点から測った高さとする。床面はなめらかで、台車は水平方向に自由に運動できる。鉛直上方及び右方を座標の正の向きとし、重力加速度の大きさをgとする。
図に示すように、高さを調節できる発射台から水平面上の台車に向けて大きさの無視できる鉄球を水平右方向に打ち出す。台車は、水平で厚みの無視できる上板およびばね定数kのばねから構成されている。上板の質量をMとし、ばねなど台車のそれ以外の部分の質量は無視できるものとする。上板はなめらかで、鉄球に対する反発係数をeとする。ばねと上板は、台車に対して鉛直方向になめらかに運動するものとする。ばねの伸縮が平衡状態のときの上板の位置を鉛直方向の座標原点とし、発射高さはこの点から測った高さとする。床面はなめらかで、台車は水平方向に自由に運動できる。鉛直上方及び右方を座標の正の向きとし、重力加速度の大きさをgとする。
上板を平衡位置で静止させた後、質量mの鉄球を発射高さHの位置から初速度 で水平方向に打ち出し、静止した台車の上板に落下させた。ただし、
で水平方向に打ち出し、静止した台車の上板に落下させた。ただし、 とする。
とする。
問1 鉄球が台車の上板に到達したとき、鉄球の速度の水平成分、鉛直成分はいくらか。
問2 鉄球が上板に衝突した直後、上板の速度の水平成分、鉛直成分はいくらか。
問3 衝突後、上板は鉛直方向には単振動した。その振幅はいくらか。本問以降の問では、一度衝突した鉄球が再び上板に衝突することはないものとする。
高さHの位置から打ち出した鉄球により上板が単振動しているとき、2つ目の質量mの鉄球を水平方向に打ち出し、その初速度を調節して台車の上板に落下させた。発射高さおよび発車時刻を調節したところ、衝突後上板の振動が止まり、振幅が0になった。
問4 2つ目の鉄球の発射高さを とするとき、高さの比
とするとき、高さの比 はいくらか。
はいくらか。
発射高さを再びHとし、上板を平衡位置で静止させる。上板には質量の無視できる電磁石が設置されていて、鉄球を吸着・切り離し、あるいは鉄球に力を加えることができるものとする。今度は上板と同じ質量Mの鉄球を初速度 で水平方向に打ち出し、静止した台車に落下させた。鉄球が上板に衝突する瞬間に、電磁石を動作させて鉄球を上板に吸着させた。
で水平方向に打ち出し、静止した台車に落下させた。鉄球が上板に衝突する瞬間に、電磁石を動作させて鉄球を上板に吸着させた。
問5 衝突直後の台車の速度はいくらか。
衝突後ばねが収縮しはじめ、最も収縮した時点で電磁石の動作を止めたところ、鉄球は上昇途中に上板を離れた。
問6 ばねが最も収縮したときの上板の鉛直方向の位置を求めよ。
問7 鉄球が上板を離れるときの上板の鉛直方向の位置を求めよ。
問8 鉄球が上板を離れるときの鉄球の速度の鉛直成分は、衝突する直前に鉄球のもつ速度の鉛直成分の何倍か。
一方、衝突後ばねが最も収縮したときから、電磁石の動作を完全には止めずに、磁力を調節して上板から鉄球に下向きに一定の力をかけ続けたところ、鉄球は上板から離れることなく単振動を続けた。
問9 鉄球が上板から離れることなく単振動を続けるのに必要な力の大きさの最小値はいくらか。 [解答へ]
慶大理工物理'11年[1]
以下の文章中の の(ア)〜(コ)に適切な式を記入しなさい。ただし、(ク)には適切な不等号(≦または≧)も記入しなさい。
の(ア)〜(コ)に適切な式を記入しなさい。ただし、(ク)には適切な不等号(≦または≧)も記入しなさい。
 図1,2のように、半径Rの半円筒面を有する質量Mの台が水平でなめらかな床に静かに置かれている。質量mの小球は床の上を進み、そのあと台の円筒面を上る。円筒の最上点をA,円筒の中心をOとする。円筒面はなめらかで、床と円筒面はなめらかに接続しており、小球と台は紙面に垂直な方向には運動しないものとする。
図1,2のように、半径Rの半円筒面を有する質量Mの台が水平でなめらかな床に静かに置かれている。質量mの小球は床の上を進み、そのあと台の円筒面を上る。円筒の最上点をA,円筒の中心をOとする。円筒面はなめらかで、床と円筒面はなめらかに接続しており、小球と台は紙面に垂直な方向には運動しないものとする。
図1のように台は床に固定された鉛直な壁に接して置かれており、台と壁が接している面はともになめらかである。小球は円筒面から離れることなく点Aまで上り、この間、台の全底面と床は接したままだった。点Bでの小球の速さをvとすると、円運動する小球が受ける向心力の大きさは である。この向心力は、小球が受ける重力のBO方向の分力と、小球が円筒面から受ける抗力との合力である。したがって、重力加速度の大きさをg,
である。この向心力は、小球が受ける重力のBO方向の分力と、小球が円筒面から受ける抗力との合力である。したがって、重力加速度の大きさをg, とすると抗力の大きさNは、
とすると抗力の大きさNは、 である。このとき、台が小球から受ける力を考えると、その鉛直方向の分力の大きさFは、Nとθ を使って、
である。このとき、台が小球から受ける力を考えると、その鉛直方向の分力の大きさFは、Nとθ を使って、 と表される。小球の初速度は図1のように右向きでその大きさは
と表される。小球の初速度は図1のように右向きでその大きさは であった。小球の力学的エネルギーが保存されることを用いて
であった。小球の力学的エネルギーが保存されることを用いて からvを消去すると、
からvを消去すると、 が得られる。(エ)は
が得られる。(エ)は で最小値をとり、また、小球が円筒面から離れることなく点Aに達したことから、
で最小値をとり、また、小球が円筒面から離れることなく点Aに達したことから、 であったことがわかる。
であったことがわかる。
(カ)〜(ク)の解答にあたっては、小球の初速度が で、小球が円筒面を上る間、台の全底面は床に接したままであったとする。この小球が点Bを通過するときのFは、
で、小球が円筒面を上る間、台の全底面は床に接したままであったとする。この小球が点Bを通過するときのFは、 と
と により、vと
により、vと を使わずに、
を使わずに、 と表すことができる。(カ)は
と表すことができる。(カ)は で最大値をとる。また、台の全底面が床と接したままであったことから、台が受ける力の鉛直方向成分を考えると、小球の質量mが不等式
で最大値をとる。また、台の全底面が床と接したままであったことから、台が受ける力の鉛直方向成分を考えると、小球の質量mが不等式 を満たしていたことがわかる。
を満たしていたことがわかる。
次に図2のように壁を取り除いた場合を考えよう。速度は右向きを正とする。最初、台は静止していた。初速度が の小球は、台の円筒面を点Cまで上り、そこから円筒面を下った。なお
の小球は、台の円筒面を点Cまで上り、そこから円筒面を下った。なお (ただし
(ただし )とする。小球が点Cに達したとき、床に対する台の速度はVだった。小球と台を合わせた全運動量が保存されることを用いると
)とする。小球が点Cに達したとき、床に対する台の速度はVだった。小球と台を合わせた全運動量が保存されることを用いると が得られる。そのあと小球は円筒面を下り、台から離れた。このときの床に対する台の速度は
が得られる。そのあと小球は円筒面を下り、台から離れた。このときの床に対する台の速度は である。
である。
[解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
