�c�嗝�H����'11�N[1]
�ȉ��̕��͒��� ��(�A)�`(�R)�ɓK�Ȏ����L�����Ȃ����B�������A(�N)�ɂ͓K�ȕs����(���܂��́�)���L�����Ȃ����B
��(�A)�`(�R)�ɓK�Ȏ����L�����Ȃ����B�������A(�N)�ɂ͓K�ȕs����(���܂��́�)���L�����Ȃ����B
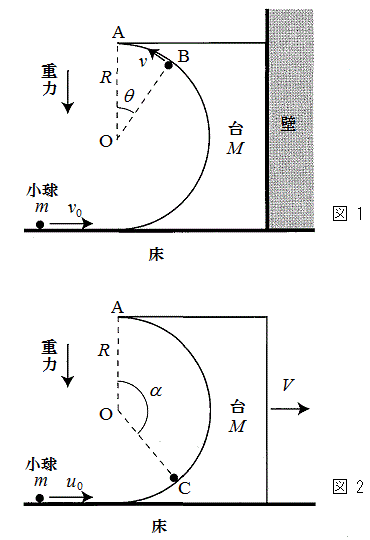 �}1�C2�̂悤�ɁA���aR�̔��~���ʂ�L���鎿��M�̑䂪�����łȂ߂炩�ȏ��ɐÂ��ɒu����Ă���B����m�̏����͏��̏��i�݁A���̂��Ƒ�̉~���ʂ����B�~���̍ŏ�_��A�C�~���̒��S��O�Ƃ���B�~���ʂ͂Ȃ߂炩�ŁA���Ɖ~���ʂ͂Ȃ߂炩�ɐڑ����Ă���A�����Ƒ�͎��ʂɐ����ȕ����ɂ͉^�����Ȃ����̂Ƃ���B
�}1�C2�̂悤�ɁA���aR�̔��~���ʂ�L���鎿��M�̑䂪�����łȂ߂炩�ȏ��ɐÂ��ɒu����Ă���B����m�̏����͏��̏��i�݁A���̂��Ƒ�̉~���ʂ����B�~���̍ŏ�_��A�C�~���̒��S��O�Ƃ���B�~���ʂ͂Ȃ߂炩�ŁA���Ɖ~���ʂ͂Ȃ߂炩�ɐڑ����Ă���A�����Ƒ�͎��ʂɐ����ȕ����ɂ͉^�����Ȃ����̂Ƃ���B
�}1�̂悤�ɑ�͏��ɌŒ肳�ꂽ�����ȕǂɐڂ��Ēu����Ă���A��ƕǂ��ڂ��Ă���ʂ͂Ƃ��ɂȂ߂炩�ł���B�����͉~���ʂ��痣��邱�ƂȂ��_A�܂ŏ��A���̊ԁA��̑S��ʂƏ��͐ڂ����܂܂������B�_B�ł̏����̑�����v�Ƃ���ƁA�~�^�����鏬��������S�͂̑傫����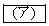 �ł���B���̌��S�͂́A��������d�͂�BO�����̕��͂ƁA�������~���ʂ����R�͂Ƃ̍��͂ł���B���������āA�d�͉����x�̑傫����g�C
�ł���B���̌��S�͂́A��������d�͂�BO�����̕��͂ƁA�������~���ʂ����R�͂Ƃ̍��͂ł���B���������āA�d�͉����x�̑傫����g�C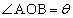 �Ƃ���ƍR�͂̑傫��N�́A
�Ƃ���ƍR�͂̑傫��N�́A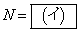 �ł���B���̂Ƃ��A�䂪���������͂��l����ƁA���̉��������̕��͂̑傫��F�́AN��θ ���g���āA
�ł���B���̂Ƃ��A�䂪���������͂��l����ƁA���̉��������̕��͂̑傫��F�́AN��θ ���g���āA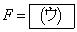 �ƕ\�����B�����̏����x�͐}1�̂悤�ɉE�����ł��̑傫����
�ƕ\�����B�����̏����x�͐}1�̂悤�ɉE�����ł��̑傫����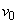 �ł������B�����̗͊w�I�G�l���M�[���ۑ�����邱�Ƃ�p����
�ł������B�����̗͊w�I�G�l���M�[���ۑ�����邱�Ƃ�p���� ����v����������ƁA
����v����������ƁA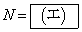 ��������B(�G)��
��������B(�G)��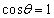 �ōŏ��l���Ƃ�A�܂��A�������~���ʂ��痣��邱�ƂȂ��_A�ɒB�������Ƃ���A
�ōŏ��l���Ƃ�A�܂��A�������~���ʂ��痣��邱�ƂȂ��_A�ɒB�������Ƃ���A �ł��������Ƃ��킩��B
�ł��������Ƃ��킩��B
(�J)�`(�N)�̉ɂ������ẮA�����̏����x�� �ŁA�������~���ʂ����ԁA��̑S��ʂ͏��ɐڂ����܂܂ł������Ƃ���B���̏������_B��ʉ߂���Ƃ���F�́A
�ŁA�������~���ʂ����ԁA��̑S��ʂ͏��ɐڂ����܂܂ł������Ƃ���B���̏������_B��ʉ߂���Ƃ���F�́A ��
��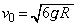 �ɂ��Av��
�ɂ��Av��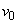 ���g�킸�ɁA
���g�킸�ɁA �ƕ\�����Ƃ��ł���B(�J)��
�ƕ\�����Ƃ��ł���B(�J)��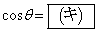 �ōő�l���Ƃ�B�܂��A��̑S��ʂ����Ɛڂ����܂܂ł��������Ƃ���A�䂪��͂̉��������������l����ƁA�����̎���m���s����
�ōő�l���Ƃ�B�܂��A��̑S��ʂ����Ɛڂ����܂܂ł��������Ƃ���A�䂪��͂̉��������������l����ƁA�����̎���m���s���� �����Ă������Ƃ��킩��B
�����Ă������Ƃ��킩��B
���ɐ}2�̂悤�ɕǂ���菜�����ꍇ���l���悤�B���x�͉E�����𐳂Ƃ���B�ŏ��A��͐Î~���Ă����B�����x�� �̏����́A��̉~���ʂ�_C�܂ŏ��A��������~���ʂ��������B�Ȃ�
�̏����́A��̉~���ʂ�_C�܂ŏ��A��������~���ʂ��������B�Ȃ� (������
(������ )�Ƃ���B�������_C�ɒB�����Ƃ��A���ɑ����̑��x��V�������B�����Ƒ�����킹���S�^���ʂ��ۑ�����邱�Ƃ�p�����
)�Ƃ���B�������_C�ɒB�����Ƃ��A���ɑ����̑��x��V�������B�����Ƒ�����킹���S�^���ʂ��ۑ�����邱�Ƃ�p�����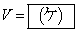 ��������B���̂��Ə����͉~���ʂ�����A�䂩�痣�ꂽ�B���̂Ƃ��̏��ɑ���������x��
��������B���̂��Ə����͉~���ʂ�����A�䂩�痣�ꂽ�B���̂Ƃ��̏��ɑ���������x�� �ł���B
�ł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�p�o�^�C�v���s�����~�^���̖��ł����A�㔼�́A�~���ʂ������Ă��܂����A�͊w�I�G�l���M�[�ۑ��A�^���ʕۑ�����l������e�ɂȂ��Ă��܂��B
(�A) ���aR�̉~���ʂ�����v�œ�������m�̏����������S���́A ......[��]
......[��]
(�C) �������S���́A���������d����BO����������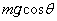 �ƁA�������~���ʂ���������R��N�Ƃ������ɓ������A
�ƁA�������~���ʂ���������R��N�Ƃ������ɓ������A ��  �@����@
�@����@ 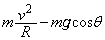 ......[��]
......[��]
(�E) �䂪������������̉��������������̑傫��F�́A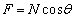 �@����A
�@����A  ......[��]
......[��]
(�G) �d�����ʒu�G�l���M�[�̊�����ʂɂƂ�ƁA���������̏�ɂ���Ƃ����͊w�I�G�l���M�[�́A�^���G�l���M�[�� �����ł��B�_B�ł��͊w�I�G�l���M�[�́A�^���G�l���M�[��
�����ł��B�_B�ł��͊w�I�G�l���M�[�́A�^���G�l���M�[�� ���ʒu�G�l���M�[
���ʒu�G�l���M�[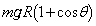 �ł��B�͊w�I�G�l���M�[�ۑ����A
�ł��B�͊w�I�G�l���M�[�ۑ����A �� 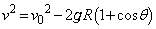 �@�ɑ�����āA
�@�ɑ�����āA  �@����B
�@����B ......[��]
......[��]
(�I) (�G)��N�� �̂Ƃ�(�_A�ɗ����Ƃ�)�A�ŏ��l
�̂Ƃ�(�_A�ɗ����Ƃ�)�A�ŏ��l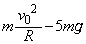 ���Ƃ�܂��B
���Ƃ�܂��B �������~���ʂ��痣��邱�ƂȂ��_A�ɒB����̂ł���A�������������R��N�́A�˂�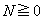 �ł��B����āA
�ł��B����āA �� 
 ......[��]
......[��]
(�J) �B��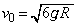 �Ƃ���ƁA
�Ƃ���ƁA B��ʉ߂���Ƃ���F�́A�A���A
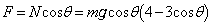
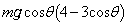 ......[��]
......[��]
(�L) (�J)�̌��ʂ��A
����́A ���A
���A �ōő�l
�ōő�l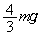 �������܂��B
�������܂��B  ......[��]
......[��]
(�N) ���̂Ƃ��A�䂪���ʂ���������R���� �Ƃ��āA�䂪�����̉����������肠������A
�Ƃ��āA�䂪�����̉����������肠������A �䂪���ʂƐڂ����܂܂ł��������Ƃ���A
�� 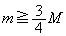 ......[��]
......[��]
(�P) �����{��̌n�̍ŏ����^�����́A�������^����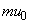 �����ł��B
�����ł��B �������_C�ɒB�����Ƃ��A���������x�̐��������ƁA������x��V�ŁA�����{����^������ �ł��B
�ł��B
�����{��ɂ́A���������ɂ��O�����������A���̕����ł��^���ʕۑ������������܂��B������A �� 
 ......[��]
......[��]
(�R) �������䂩�痣�ꂽ��̑�����x�� �Ƃ��܂��B�͊w�I�G�l���M�[���ۑ�����邱�Ƃ���A�����Ƒ�̉^�����W��1�̏Փ˂ƌ��Ȃ��ƁA�����W���̎����A
�Ƃ��܂��B�͊w�I�G�l���M�[���ۑ�����邱�Ƃ���A�����Ƒ�̉^�����W��1�̏Փ˂ƌ��Ȃ��ƁA�����W���̎����A 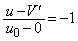 �@��
�@��  �@����C
�@����C�C���A
�� 
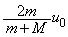 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B