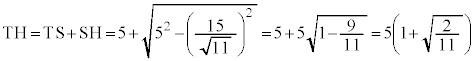�@���ʃe�X�g���wIA '23�N��1��@
[1]�@����x�ɂ��Ă̕s����
�̉���
�ł���B
����āA����a�Cb�Cc�Cd��
�����Ă���Ƃ��A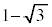 �͕��ł��邱�Ƃɒ��ӂ���ƁA
�͕��ł��邱�Ƃɒ��ӂ���ƁA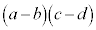 �̂Ƃ蓾��l�͈̔͂�
�̂Ƃ蓾��l�͈̔͂� �ł��邱�Ƃ��킩��B
����
 �@����@
�@����@�ł���Ƃ��A�����
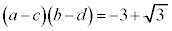 �@����A
�@����A�����藧�Ȃ��
 �@����B
�@����B�ł��邱�Ƃ��A�����@�C�A�C�B�̍��ӂ�W�J���Ĕ�r���邱�Ƃɂ��킩��B
[2](1) �_O�𒆐S�Ƃ��A���a��5�ł���~O������B���̉~�����2�_A�CB��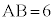 �ƂȂ�悤�ɂƂ�B�܂��A�~O�̉~����ɁA2�_A�CB�Ƃ͈قȂ�_C���Ƃ�B
�ƂȂ�悤�ɂƂ�B�܂��A�~O�̉~����ɁA2�_A�CB�Ƃ͈قȂ�_C���Ƃ�B
(i) 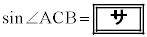 �ł���B�܂��A�_C��
�ł���B�܂��A�_C��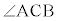 ���݊p�ƂȂ�悤�ɂƂ�Ƃ��A
���݊p�ƂȂ�悤�ɂƂ�Ƃ��A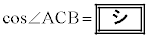 �ł���B
�ł���B
(ii) �_C����ABC�̖ʐς��ő�ƂȂ�悤�ɂƂ�B�_C���璼��AB�ɐ����Ȓ����������A����AB�Ƃ̌�_��D�Ƃ���Ƃ��A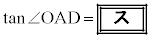 �ł���B�܂��A��ABC�̖ʐς�
�ł���B�܂��A��ABC�̖ʐς� �ł���B
�ł���B  �̉Q(�������̂��J��Ԃ��I��ł��悢�B)
�̉Q(�������̂��J��Ԃ��I��ł��悢�B) �@
�@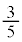 �@�@
�@�@ �@
�@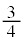 �@�@
�@�@ �@
�@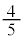 �@�@
�@�@ �@1�@�@
�@1�@�@ �@
�@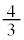
 �@
�@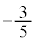 �@�@
�@�@ �@
�@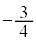 �@�@
�@�@ �@
�@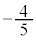 �@�@
�@�@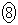 �@
�@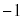 �@�@
�@�@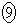 �@
�@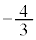
(2) ���a��5�ł��鋅S������B���̋��ʏ��3�_P�CQ�CR���Ƃ����Ƃ��A������3�_��ʂ镽��α���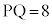 �C
�C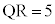 �C
�C �ł������Ƃ���B
�ł������Ƃ���B ��S�̋��ʏ�ɓ_T���O�p��TPQR�̑̐ς��ő�ƂȂ�悤�ɂƂ�Ƃ��A���̑̐ς����߂悤�B
�܂��A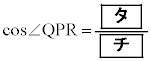 �ł��邱�Ƃ���A��PQR�̖ʐς�
�ł��邱�Ƃ���A��PQR�̖ʐς�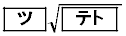 �ł���B
�ł���B
���ɁA�_T���畽��α�ɐ����Ȓ����������A����α�Ƃ̌�_��H�Ƃ���B���̂Ƃ��APH�CQH�CRH�̒����ɂ��āA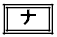 �����藧�B
�����藧�B
�ȏ���A�O�p��TPQR�̑̐ς� �ł���B
�ł���B
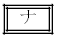 �̉Q
�̉Q  �@
�@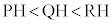 �@�@
�@�@ �@
�@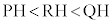
 �@
�@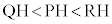 �@�@
�@�@ �@
�@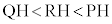
 �@
�@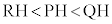 �@�@
�@�@ �@
�@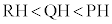
 �@
�@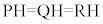
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�O���́A�W�J���Ă݂�ƁA�Ƃ����q���g������̂ʼn��ł��Ȃ��ł��傤�B�㔼�́A��Ԑ}�`�Ƃ͌����Ă��A���̒��S���狅�ʏ��3�_������łł���O�p�`�ɐ��������낷�ƊO�S�ɗ��邱�Ƃ�m���Ă���A�����藝�E�]���藝���g���݂̂ʼn������܂��B
�� 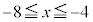 �@�A�C
�@�A�C 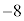 ......[��]�@�E�G
......[��]�@�E�G 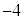 ......[��]
......[��] �C��x��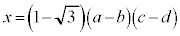 �Ƃ��āA
�Ƃ��āA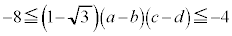
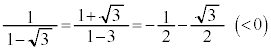 ���A
���A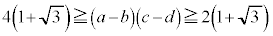 �C�܂�A
�C�܂�A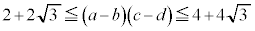 �@�I 2�@�J 2�@�L 4�@�N 4 ......[��]
�@�I 2�@�J 2�@�L 4�@�N 4 ......[��]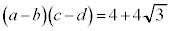 �C
�C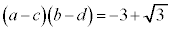 �ł���Ƃ��A�ӁX�������Ƃɂ��A
�ł���Ƃ��A�ӁX�������Ƃɂ��A �P 7�@�R 3 ......[��]
[2](1)(i) ��ACB�̊O�ډ~���~O�ł��邱�ƂƁA�����藝���A 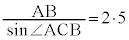 �@��
�@�� 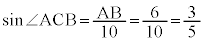 �@�T0 ......[��]
�@�T0 ......[��]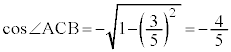 �@(�O�p�����Q��)�@�V 7 .......[��]
�@(�O�p�����Q��)�@�V 7 .......[��](ii) �_C����ABC�̖ʐς��ő�ƂȂ�悤�ɂƂ�Ƃ��A��ABC��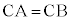 �ł���ӎO�p�`�ŁA�_C���璼��AB�ɐ���AD�����낷��D�́AAB�̒��_�ł��B
�ł���ӎO�p�`�ŁA�_C���璼��AB�ɐ���AD�����낷��D�́AAB�̒��_�ł��B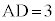 �C
�C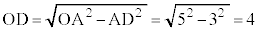 ���A
���A 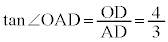 �@�X 4 ......[��]
�@�X 4 ......[��]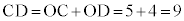
���A��ABC�̖ʐς́A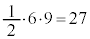 �@�Z�\ 27 ......[��]
�@�Z�\ 27 ......[��]
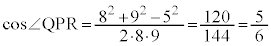 �@�^ 5�@�` 6 ......[��]
�@�^ 5�@�` 6 ......[��]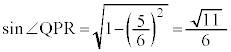
��PQR���ʐ��́A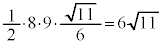 �@�c 6�@�e�g 11 ......[��]�_T���畽��α�ɐ����Ȓ����������A����α�Ƃ̌�_��H�Ƃ���ƁA�_H�́�PQR�̊O�S�ł��B�܂�A
�@�c 6�@�e�g 11 ......[��]�_T���畽��α�ɐ����Ȓ����������A����α�Ƃ̌�_��H�Ƃ���ƁA�_H�́�PQR�̊O�S�ł��B�܂�A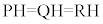 �ł��B�@�i 6 ......[��]��PQR�̊O�ډ~�̔��a��r�Ƃ���ƁA�����藝���A
�ł��B�@�i 6 ......[��]��PQR�̊O�ډ~�̔��a��r�Ƃ���ƁA�����藝���A 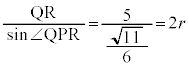 �@��
�@�� 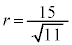
��S�̒��S��S�Ƃ��āA�O�p��TPQR�̑̐ς��ő�ƂȂ�Ƃ��AT�CS�CH�͈꒼����ɕ��т܂��B�O�p��TPQR�̍���TH�́A
�O�p��TPQR�̑̐ς́A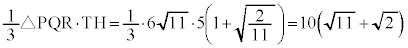
�j�k 10�@�l�m 11�@�n 2 ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 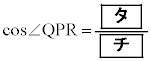 �ł��邱�Ƃ���A��PQR�̖ʐς�
�ł��邱�Ƃ���A��PQR�̖ʐς�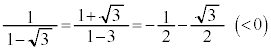 ���A
���A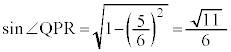
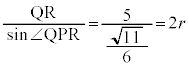 �@��
�@��