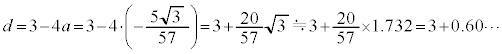�@���ʃe�X�g���w IA '23 �N�� 2 ��@ [1] �@���Y����́A�����Ȃ����\���Ă��� 2020 �N�̉ƌv�����̌��ʂ�p���āA�n��ɂ��H�����̈Ⴂ�ɂ��čl���Ă���B�ƌv�����ɂ����钲���n�_�́A�s���{�������ݎs����ѐ��ߎw��s�s ( �s���{�������ݎs������ ) �ł���A���v 52 �s�ł���B�ƌv�����̌��ʂ̒��ł��A�X�[�p�[�}�[�P�b�g�ȂǂŔ̔�����Ă��钲���H�i�́u��l�ȏ�̐��т� 1 ���ѓ�����N�Ԏx�o���z ( �ȉ��A�x�o���z�A�P�ʂ͉~ ) �v�͂��邱�Ƃɂ����B�ȉ��ɂ����ẮA 52 �s�̒����H�i�̎x�o���z���f�[�^�Ƃ��ėp����B
���Y����͒����H�i�Ƃ��āA�ŏ��ɂ��Ȃ��̂��ΏĂ� ( �ȉ��A���ΏĂ� ) �ɒ��ڂ��A�} 1 �̂悤�� 52 �s�ɂ����邩�ΏĂ��̎x�o���z�̃q�X�g�O�������쐬�����B�������A�q�X�g�O�����̊e�K���̋�Ԃ́A�����̐��l���܂݁A�E���̐��l���܂܂Ȃ��B Web �y�[�W�����Ƃɍ쐬���Ă���B (1) �} 1 ���玟�̂��Ƃ��ǂݎ���B
�E�� 1 �l���ʐ����܂܂��K���� �E�� 3 �l���ʐ����܂܂��K���� �E�l���ʔ͈͂� �C ( �������̂��J��Ԃ��I��ł��悢 ) �@ 1000 �ȏ� 1400 �����@�@ 1400 �ȏ� 1800 ���� 1800 �ȏ� 2200 �����@�@ 2200 �ȏ� 2600 ���� 2600 �ȏ� 3000 �����@�@ 3000 �ȏ� 3400 ���� 3400 �ȏ� 3800 �����@�@ 3800 �ȏ� 4200 ���� 4200 �ȏ� 4600 �����@�@ 4600 �ȏ� 5000 ���� �̉Q �@ 800 ��菬���� �@ 800 ���傫�� 1600 ��菬���� �@ 1600 ���傫�� 2400 ��菬���� �@ 2400 ���傫�� 3200 ��菬���� �@ 3200 ���傫�� 4000 ��菬���� �@ 4000 ���傫��
(2)(i) ���Y����́A�����ł̒n��ɂ��H�����̈Ⴂ�ׂ邽�߂ɁA 52 �s�𓌑��̒n�� E(19 �s ) �Ɛ����̒n�� W(33 �s ) �̓�ɕ����čl���邱�Ƃɂ����B
(i) �n�� E �ƒn�� W �ɂ��āA���ΏĂ��̎x�o���z�̔��Ђ��}���A�} 2 �C�} 3 �̂悤�ɂ��ꂼ��쐬�����B 2 �Ɛ} 3 ����ǂݎ��邱�ƂƂ��āA���� �@�n�� E �ɂ����āA������������ 5 �Ԗڂ� 2000 �ȉ��ł���B �@�n�� E �ƒn�� W �͈͓̔͂������B �@�����l�́A�n�� E ���n�� W �̕����傫���B �@ 2600 �����̎s�̊����́A�n�� E ���n�� W �̕����傫���B
(ii) ���Y����́A�n�� E �ƒn�� W �̃f�[�^�̎U���̓x�����𐔒l�łƂ炦�悤�Ǝv���A���ꂼ��̕��U���l���邱�Ƃɂ����B�n�� E �ɂ����邩�ΏĂ��̎x�o���z�̕��U�́A�n�� E �̂��ꂼ��̎s�ɂ����邩�ΏĂ��̎x�o���z�̕��� �̉Q �@ 2 ������v�����l �@��Βl�����v�����l �@ 2 ������v���Ēn�� E �̎s�̐��Ŋ������l �@��Βl�����v���Ēn�� E �̎s�̐��Ŋ������l �@ 2 ������v���Ēn�� E �̎s�̐��Ŋ������l�̕������̂������̂��� �@��Βl�����v���Ēn�� E �̎s�̐��Ŋ������l�̕������̂������̂���
(3) ���Y����́A (2) �ōl�����n�� E �ɂ�����A�₫�Ƃ�̎x�o���z�ɂ��Ă����ׂ邱�Ƃɂ����B
�����ł͒n�� E �ɂ����āA�₫�Ƃ�̎x�o���z����������A���ΏĂ��̎x�o���z����������X��������̂ł͂Ȃ����ƍl���A�܂��} 4 �̂悤�ɁA�n�� E �ɂ�����A�₫�Ƃ�Ƃ��ΏĂ��̎x�o���z�̎U�z�}���쐬�����B�����āA���W�����v�Z���邽�߂ɁA�\ 1 �̂悤�ɕ��ϒl�A���U�A�W��������ы����U���Z�o�����B�������A�����U�͒n�� E �̂��ꂼ��̎s�ɂ�����₫�Ƃ�̎x�o���z�̕��Ƃ��ΏĂ��̎x�o���z�̕��Ƃ̐ς̕��ϒl�ł���B 1 ��p����ƁA�n�� E �ɂ�����A�₫�Ƃ�̎x�o���z�Ƃ��ΏĂ��̎x�o���z�̑��W���� �@
[2] �@���Y����ƉԎq����́A�o�X�P�b�g�{�[���̃v���I��̒��ɂ́A�����O�Ɠ��������ŃV���[�g��łĂ�l�����邱�Ƃ�m��A�V���[�g��ł����ɂ���ă{�[���̋O�����ǂ��ς�邩�ɂ��čl���Ă���B
��l�́A�} 1 �̂悤�ɍ��W������߂�ꂽ���ʏ�ɁA�v���I��ƉԎq���V���[�g��łl�q��^�����猩���}�������A�{�[���������O�ɓ������ꍇ�ɂ��āA��� ���� ��ݒ肵�čl���邱�Ƃɂ����B�����̒P�ʂ̓��[�g���ł��邪�A�ȉ��ł͏ȗ�����B ���� �|�|�|�|�|�|�|�|�|�|�|�|�| �E���ʏ�ł́A�{�[���a 0.2 �̉~�Ƃ���B
�E�����O��^�����猩���Ƃ��̍��[��_ A �C�E�[��_ B �Ƃ��A�����O�̑����͖�������B �E�{�[���������O�⑼�̂��̂ɓ����炸�ɏォ�烊���O��ʂ�A���{�[���̒��S�� AB �̒��_ M ��ʂ�ꍇ���l����B�������A�{�[���������O�ɓ�����Ƃ́A�{�[���̒��S�� A �܂��� B �Ƃ̋����� 0.1 �ȉ��ɂȂ邱�ƂƂ���B �E�v���I�肪�V���[�g��łꍇ�̃{�[���̒��S��_ P �Ƃ��A P �́A�͂��߂ɓ_ M ��ʂ�A��ɓʂ̕������� P �� �E�Ԏq���V���[�g��łꍇ�̃{�[���̒��S��_ H �Ƃ��A H �́A�͂��߂ɓ_ M ��ʂ�A��ɓʂ̕������� H �� �E������ y ���W���u �V���[�g�̍��� �v�Ƃ��A���_�� x ���W���u �{�[�����ł������Ȃ�Ƃ��̒n��̈ʒu �v�Ƃ���B �|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|
(1) ������ a �Ƃ���B������ �ƕ\�����Ƃ��ł���B�܂��A�v���I��́u �V���[�g�̍��� �v��
�ł���B p �Ƃ���B������ �ƕ\�����Ƃ��ł���B �{�[�����ł������Ȃ�Ƃ��̒n��̈ʒu �v�̔�r�̋L�q�Ƃ��āA���� �@�v���I��ƉԎq����́u �{�[�����ł������Ȃ�Ƃ��̒n��̈ʒu �v�́A�˂Ɉ�v����B �@�v���I��́u �{�[�����ł������Ȃ�Ƃ��̒n��̈ʒu �v�̕����A�˂� M �� x ���W�ɋ߂��B �@�Ԏq����́u �{�[�����ł������Ȃ�Ƃ��̒n��̈ʒu �v�̕����A�˂� M �� x ���W�ɋ߂��B �@�v���I��́u �{�[�����ł������Ȃ�Ƃ��̒n��̈ʒu �v�̕��� M �� x ���W�ɋ߂��Ƃ�������A�Ԏq����́u �{�[�����ł������Ȃ�Ƃ��̒n��̈ʒu �v�̕��� M �� x ���W�ɋ߂��Ƃ�������B
(2) ��l�́A�{�[���������O���ꂷ���ʂ�ꍇ�̃v���I��ƉԎq����́u �V���[�g�̍��� �v�ɂ��Ď��̂悤�ɘb���Ă���B
�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|
���Y�F�Ⴆ�A�v���I��̃{�[���������O�ɓ�����Ȃ��悤�ɂ���ɂ́A P �������O�̍��[ A �̂ǂ̂��炢���ʂ�Ηǂ��̂��ȁB �Ԏq�F A �̐^��̓_�� P ���ʂ�_ D ���A���� DM �� A �𒆐S�Ƃ��锼�a 0.1 �̉~�Ɛڂ���悤�ɂƂ��čl���Ă݂���ǂ����ȁB
���Y�F�Ȃ�قǁB P �̋O���͏�ɓʂ̕������ŎR�Ȃ肾����A���̏ꍇ�A�} 2 �̂悤�ɁA P �� D ��ʂ�����Ő��� DM ���㑤��ʂ�̂Ń{�[���̓����O�ɓ�����Ȃ��ˁB�Ԏq����̏ꍇ���A H ������ D ��ʂ�A�{�[���̓����O�ɓ�����Ȃ��ˁB
�Ԏq�F������ D ��ʂ�ꍇ�Ńv���I��Ǝ��́u �V���[�g�̍��� �v���ׂĂ݂悤��B �|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|
�} 2 �̂悤�ɁA M ��ʂ钼�� A �𒆐S�Ƃ��锼�a 0.1 �̉~�ɒ��� AB �̏㑤�Őڂ��Ă���Ƃ���B�܂��A A ��ʂ蒼�� AB �ɐ����Ȓ����������A D �Ƃ���B���̂Ƃ��A D ��ʂ�Ƃ��A �ƂȂ�B D ��ʂ�Ƃ��A (1) �ŗ^����ꂽ �V���[�g�̍��� �v�͖� 3.4 �Ƌ��߂���B D ��ʂ�Ƃ��A�v���I��ƉԎq����́u �V���[�g�̍��� �v���ׂ�ƁA �V���[�g�̍��� �v�̕����傫���A���̍��̓{�[�� 1 ���@�@ <@1>> �@�� 2 ���@�@ 3 ���@�@ 4 �� �y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�� �@ [1] ( �p��ɂ��Ă� �f�[�^�̐��� ���Q�� ) �͗e�Ղł����A [2] �́A���X�l�����ޏ�Ɏ��v�Z�œ�����͖̂����Ȃ̂ŁA�o��҂̈Ӑ}�ɍ��킹�ď��ɍl����K�v������܂��B��蕶���� [1](1) �f�[�^�̑傫���� 52 �ŋ����Ȃ̂ŁA �����l �� 26 �Ԗڂ� 27 �Ԗڂ̕��ςŁA �� 1 �l���ʐ� �� 13 �Ԗڂ� 14 �Ԗڂ̕��ρA �� 3 �l���ʐ� �� 39 �Ԗڂ� 40 �Ԗڂ̕��ςɂȂ�܂��B 13 �Ԗڂ� 14 �Ԗڂ��܂ފK���� 1800 �` 2200( �C 39 �Ԗڂ� 40 �Ԗڂ��܂ފK���� 3000 �` 3400( �C�@�A 2 �@�C 5 ......[ �� ] �l���ʔ͈� �́A�ł������� 2200 �` 3000 �C�ł��L���� 1800 �` 3400 �C����āA 800 ���傫�� 1600 ��菬���� ( �̂ŁA�E 1 ......[ �� ]
(2)(i) �n�� E �̃f�[�^�̑傫���� 19 �Ȃ̂ŁA�� 1 �l���ʐ��� 5 �ԖڂŐ} 2 ���� 2050 ���炢�ł��B����� �} 2 ���A�n�� E �͈̔͂́A�ŏ��l�� 1180 ���x�A�ő�l�� 3700 ���x�ŁA�͈͂� 2520 ���x�A�} 3 ���n�� W �͈̔͂́A�ŏ��l�� 1380 ���x�A�ő�l�� 4980 ���x�ŁA�͈͂� 3600 ���x�Ŗ��炩�ɗ��҂͓������Ȃ��̂ŁA 2 ���n�� E �̒����l�� 2250 ���x�A�} 3 ���n�� W �̒����l�� 2620 ���x�A�����l�͒n�� E ���n�� W �̕����傫���A E �̒����l�� 2600 ��菬�����ߔ����� 2600 �����ł��B�n�� W �̒����l�� 2600 ���傫���A���Ȃ��Ƃ������� 2600 �����ł��B����āA 2600 �����̎s�̊����͒n�� E �̕����傫���A 2 ......[ �� ]
(ii) ���U �́A���� 2 ��̘a���f�[�^�̑傫���Ŋ��������̂ł��B�@�I 2 ......[ �� ]
�@�J 7 ......[ �� ]
[2](1) �v���I��̓����O�Ɠ�����������V���[�g��ł̂ŁA������ �{�[�����ł������Ȃ�Ƃ��̒n��̈ʒu �v�́A ( 2 ���� ���Q�� ) �B������ y ���W�A�����v���I��́u �V���[�g�̍��� �v�� d �Ƃ��āA �@����@ �̂Ƃ� �@�� �L 4 �@�N 3 �@�P 4 �@�R 3 ......[ �� ] ������Ŗ��������̂ɕK�v����܂��A��蕶�ɏ����Ă�������� y ���W�� �̂Ƃ� �ӁX�����ƁA
����āA �{�[�����ł������Ȃ�Ƃ��̒n��̈ʒu �v�́A�Ԏq����̕����A M �� x ���W 2 ......[ �� ]
(2) ���Y����ƉԎq����̉�b�́A M ��ʂ��ɓʂȕ������Ȃ̂ŁA M ��ʂ�~ ( �_ A �𒆐S�Ƃ��锼�a 0.1 �̉~ ) �̐ڐ� D( ����� ) �� ���肬���ʉ߂��ă����O�ɓ���ꍇ ( �_ D ��ʉ߂��� ) �A AD �͖�蕶�ɏ����Ă���̂ŁA������ŋ��߂�K�v�͂���܂��A T �Ƃ��āA [ �P ][ �R ] �� �@�� �@�V 5 �@�X 3 �@�Z�\ 57 ......[ �� ] �܂�A�v���I��́u �V���[�g�̍��� �v�͂ق� 3.6 �ł��B�Ԏq����̕��́A�A�ŁA p �ƒ��_�� y ���W�����߂�̂́A���܂�Ɍv�Z����ςȂ̂ŁA��蕶�ɗ^�����Ă��� �V���[�g�̍��� �v�́A�v���I��̕����ق� ( �{�[�� 1 �� ) ���������A�^ 0 �@�` 0 ......[ �� ] �y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@ ���w TOP �@�@ TOP �y�[�W�ɖ߂� �y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B �e���̒��쌠�� © 2005-2024 (�L)����� ��w�y�w�m ���������t���I ���n��w�l�b�g�m ��w�y�w�m (���ē��������� )������́A������܂Ń��[�� �� 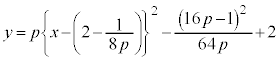
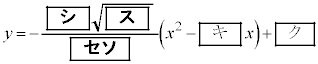
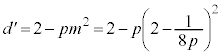
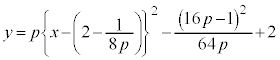 �@����A
�@����A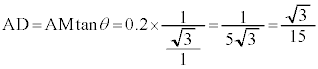
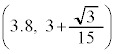 ��ʂ�ƍl����̂ł͌v�Z���ʓ|�Ȃ̂ŁA�������̎��Ɋւ���Ώ̓_
��ʂ�ƍl����̂ł͌v�Z���ʓ|�Ȃ̂ŁA�������̎��Ɋւ���Ώ̓_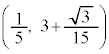 ��ʉ߂���ƍl����ƁA[�P][�R]��
��ʉ߂���ƍl����ƁA[�P][�R]��