大学入学共通テスト数学IA 2024年問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1][1] 不等式
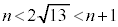 ・・・①
・・・①を満たす整数nは である。実数a,bを
である。実数a,bを 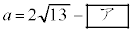 ・・・②
・・・②
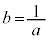 ・・・③
・・・③で定める。このとき
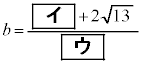 ・・・④
・・・④である。また
である。
①から
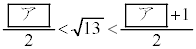 ・・・⑤
・・・⑤が成り立つ。
太郎さんと花子さんは、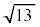 について話している。
について話している。
太郎:⑤から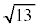 のおよその値がわかるけど、小数点以下はよくわからないね。
のおよその値がわかるけど、小数点以下はよくわからないね。 花子:小数点以下をもう少し詳しく調べることができないかな。
①と④から
を満たす整数mは となる。よって、③から
となる。よって、③から 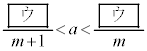 ・・・⑥
・・・⑥が成り立つ。
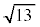 の整数部分は
の整数部分は であり、②と⑥を使えば
であり、②と⑥を使えば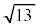 の小数第1位の数字は
の小数第1位の数字は ,小数第2位の数字は
,小数第2位の数字は であることがわかる。
であることがわかる。
[2] 以下の問題を解答するにあたっては、必要に応じて問題末の三角比の表を用いてもよい。
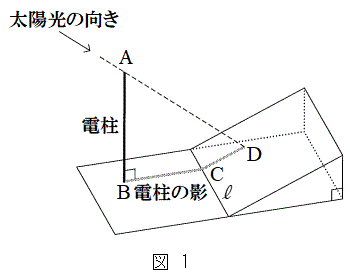 水平な地面(以下、地面)に垂直に立っている電柱の高さを、その影の長さと太陽高度を利用して求めよう。
水平な地面(以下、地面)に垂直に立っている電柱の高さを、その影の長さと太陽高度を利用して求めよう。
図1のように、電柱の影の先端は坂の斜面(以下、坂)にあるとする。また、坂には傾斜を表す道路標識が設置されていて、そこには7%と表示されているとする。
電柱の太さと影の幅は無視して考えるものとする。また、地面と坂は平面であるとし、地面と坂が交わってできる直線を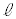 とする。
とする。
電柱の先端を点Aとし、根もとを点Bとする。電柱の影について、地面にある部分を線分BCとし、坂にある部分を線分CDとする。線分BC,CDがそれぞれ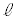 と垂直であるとき、電柱の影は坂に向ってまっすぐにのびているということにする。
と垂直であるとき、電柱の影は坂に向ってまっすぐにのびているということにする。
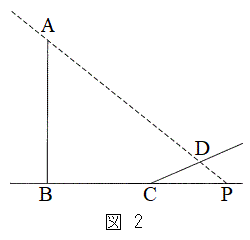 電柱の影が坂に向ってまっすぐにのびているとする。このとき、4点A,B,C,Dを通る平面は
電柱の影が坂に向ってまっすぐにのびているとする。このとき、4点A,B,C,Dを通る平面は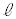 と垂直である。その平面において、図2のように、直線ADと直線BCの交点をPとすると、太陽高度とは
と垂直である。その平面において、図2のように、直線ADと直線BCの交点をPとすると、太陽高度とは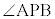 の大きさのことである。
の大きさのことである。
道路標識の7%という表示は、この坂をのぼったとき、100mの水平距離に対いて7mの割合で高くなることを示している。nを1以上9以下の整数とするとき、坂の傾斜角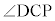 の大きさについて
の大きさについてを満たすnの値は である。
である。
以下では、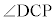 の大きさは、ちょうど
の大きさは、ちょうど であるとする。
であるとする。
ある日、電柱の影が坂に向ってまっすぐにのびていたとき、影の長さを調べたところ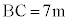 ,
,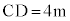 であり、太陽高度は
であり、太陽高度は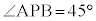 であった。点Dから直線ABに垂直な直線を引き、直線ABとの交点をEとするとき
であった。点Dから直線ABに垂直な直線を引き、直線ABとの交点をEとするとき であり
である。よって、電柱の高さは、小数第2位で四捨五入すると であることがわかる。
であることがわかる。
 ,
, の解答群(同じものを繰り返し選んでもよい。)
の解答群(同じものを繰り返し選んでもよい。)
 の解答群
の解答群 10.4
10.4  10.7
10.7  11.0
11.0 11.3
11.3  11.6
11.6  11.9
11.9別の日、電柱の影が坂に向ってまっすぐにのびていたときの太陽高度は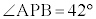 であった。電柱の高さがわかったので、前回調べた日からの影の長さの変化を知ることができる。電柱の影について、坂にある部分の長さは
であった。電柱の高さがわかったので、前回調べた日からの影の長さの変化を知ることができる。電柱の影について、坂にある部分の長さは である。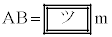 として、これを計算することにより、この日の電柱の影について、坂にある部分の長さは、前回調べた4mより約1.2mだけ長いことがわかる。
として、これを計算することにより、この日の電柱の影について、坂にある部分の長さは、前回調べた4mより約1.2mだけ長いことがわかる。
 ,
, の解答群(同じものを繰り返し選んでもよい。)
の解答群(同じものを繰り返し選んでもよい。)
三角比の表
| 角 | 正弦(sin) | 余弦(cos) | 正接(tan) | | 角 | 正弦(sin) | 余弦(cos) | 正接(tan) |
| 0° | 0.0000 | 1.0000 | 0.0000 | | 45° | 0.7071 | 0.7071 | 1.0000 |
| 1° | 0.0175 | 0.9998 | 0.0175 | | 46° | 0.7193 | 0.6947 | 1.0355 |
| 2° | 0.0349 | 0.9994 | 0.0349 | | 47° | 0.7314 | 0.6820 | 1.0724 |
| 3° | 0.0523 | 0.9986 | 0.0524 | | 48° | 0.7431 | 0.6691 | 1.1106 |
| 4° | 0.0698 | 0.9976 | 0.0699 | | 49° | 0.7547 | 0.6561 | 1.1504 |
| 5° | 0.0872 | 0.9962 | 0.0875 | | 50° | 0.7660 | 0.6428 | 1.1918 |
| 6° | 0.1045 | 0.9945 | 0.1051 | | 51° | 0.7771 | 0.6293 | 1.2349 |
| 7° | 0.1219 | 0.9925 | 0.1228 | | 52° | 0.7880 | 0.6157 | 1.2799 |
| 8° | 0.1392 | 0.9903 | 0.1405 | | 53° | 0.7986 | 0.6018 | 1.3270 |
| 9° | 0.1564 | 0.9877 | 0.1584 | | 54° | 0.8090 | 0.5878 | 1.3764 |
| 10° | 0.1736 | 0.9848 | 0.1763 | | 55° | 0.8192 | 0.5736 | 1.4281 |
| 11° | 0.1908 | 0.9816 | 0.1944 | | 56° | 0.8290 | 0.5592 | 1.4826 |
| 12° | 0.2079 | 0.9781 | 0.2126 | | 57° | 0.8387 | 0.5446 | 1.5399 |
| 13° | 0.2250 | 0.9744 | 0.2309 | | 58° | 0.8480 | 0.5299 | 1.6003 |
| 14° | 0.2419 | 0.9703 | 0.2493 | | 59° | 0.8572 | 0.5150 | 1.6643 |
| 15° | 0.2588 | 0.9659 | 0.2679 | | 60° | 0.8660 | 0.5000 | 1.7321 |
| 16° | 0.2756 | 0.9613 | 0.2867 | | 61° | 0.8746 | 0.4848 | 1.8040 |
| 17° | 0.2924 | 0.9563 | 0.3057 | | 62° | 0.8829 | 0.4695 | 1.8807 |
| 18° | 0.3090 | 0.9511 | 0.3249 | | 63° | 0.8910 | 0.4540 | 1.9626 |
| 19° | 0.3256 | 0.9455 | 0.3443 | | 64° | 0.8988 | 0.4384 | 2.0503 |
| 20° | 0.3420 | 0.9397 | 0.3640 | | 65° | 0.9063 | 0.4226 | 2.1445 |
| 21° | 0.3584 | 0.9336 | 0.3839 | | 66° | 0.9135 | 0.4067 | 2.2460 |
| 22° | 0.3746 | 0.9272 | 0.4040 | | 67° | 0.9205 | 0.3907 | 2.3559 |
| 23° | 0.3907 | 0.9205 | 0.4245 | | 68° | 0.9272 | 0.3746 | 2.4751 |
| 24° | 0.4067 | 0.9135 | 0.4452 | | 69° | 0.9336 | 0.3584 | 2.6051 |
| 25° | 0.4226 | 0.9063 | 0.4663 | | 70° | 0.9397 | 0.3420 | 2.7475 |
| 26° | 0.4384 | 0.8988 | 0.4877 | | 71° | 0.9455 | 0.3256 | 2.9042 |
| 27° | 0.4540 | 0.8910 | 0.5095 | | 72° | 0.9511 | 0.3090 | 3.0777 |
| 28° | 0.4695 | 0.8829 | 0.5317 | | 73° | 0.9563 | 0.2924 | 3.2709 |
| 29° | 0.4848 | 0.8746 | 0.5543 | | 74° | 0.9613 | 0.2756 | 3.4874 |
| 30° | 0.5000 | 0.8660 | 0.5774 | | 75° | 0.9659 | 0.2588 | 3.7321 |
| 31° | 0.5150 | 0.8572 | 0.6009 | | 76° | 0.9703 | 0.2419 | 4.0108 |
| 32° | 0.5299 | 0.8480 | 0.6249 | | 77° | 0.9744 | 0.2250 | 4.3315 |
| 33° | 0.5446 | 0.8387 | 0.6494 | | 78° | 0.9781 | 0.2079 | 4.7046 |
| 34° | 0.5592 | 0.8290 | 0.6745 | | 79° | 0.9816 | 0.1908 | 5.1446 |
| 35° | 0.5736 | 0.8192 | 0.7002 | | 80° | 0.9848 | 0.1736 | 5.6713 |
| 36° | 0.5878 | 0.8090 | 0.7265 | | 81° | 0.9877 | 0.1564 | 6.3138 |
| 37° | 0.6018 | 0.7986 | 0.7536 | | 82° | 0.9903 | 0.1392 | 7.1154 |
| 38° | 0.6157 | 0.7880 | 0.7813 | | 83° | 0.9925 | 0.1219 | 8.1443 |
| 39° | 0.6293 | 0.7771 | 0.8098 | | 84° | 0.9945 | 0.1045 | 9.5144 |
| 40° | 0.6428 | 0.7660 | 0.8391 | | 85° | 0.9962 | 0.0872 | 11.4301 |
| 41° | 0.6561 | 0.7547 | 0.8693 | | 86° | 0.9976 | 0.0698 | 14.3007 |
| 42° | 0.6691 | 0.7431 | 0.9004 | | 87° | 0.9986 | 0.0523 | 19.0811 |
| 43° | 0.6820 | 0.7314 | 0.9325 | | 88° | 0.9994 | 0.0349 | 28.6363 |
| 44° | 0.6947 | 0.7193 | 0.9657 | | 89° | 0.9998 | 0.0175 | 57.2900 |
| 45° | 0.7071 | 0.7071 | 1.0000 | | 90° | 1.0000 | 0.0000 | - |
[解答へ]
[2][1] 座標平面上に4点O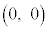 ,A
,A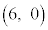 ,B
,B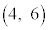 ,C
,C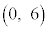 を頂点とする台形OABCがある。また、この座標平面上で、点P,点Qは次の規則に従って移動する。
を頂点とする台形OABCがある。また、この座標平面上で、点P,点Qは次の規則に従って移動する。
-規則-------------
・Pは、Oから出発して毎秒1の一定の速さでx軸上を正の向きにAまで移動し、Aに到達した時点で移動を終了する。
・Qは、Cから出発してy軸上を負の向きにOまで移動し、Oに到達した後はy軸上を正の向きにCまで移動する。そして、Cに到達した時点で移動を終了する。ただし、Qは毎秒2の一定の速さで移動する。
・P,Qは同時刻に移動を開始する。
----------------
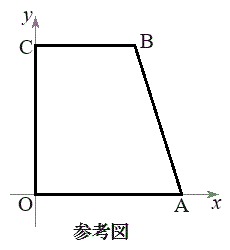 この規則に従ってP,Qが移動するとき、P,QはそれぞれA,Cに同時刻に到達し、移動を終了する。
この規則に従ってP,Qが移動するとき、P,QはそれぞれA,Cに同時刻に到達し、移動を終了する。
以下において、P,Qが移動を開始する時刻を開始時刻、移動を終了する時刻を終了時刻とする。
(1) 開始時刻から1秒後の△PBQの面積は である。
である。
(2) 開始時刻から3秒間の△PBQの面積について、面積の最小値は であり、最大値は
であり、最大値は である。
である。
(3) 開始時刻から終了時刻までの△PBQの面積について、面積の最小値は であり、最大値は
であり、最大値は である。
である。
(4) 開始時刻から終了時刻までの△PBQの面積について、面積が10以下となる時間は 秒間である。
秒間である。
[2] 高校の陸上部で長距離競技の選手として活躍する太郎さんは、長距離競技の公認記録を調査した。調査したある長距離競技での公認記録を、その選手のその競技でのベストタイムということにする。
(1) 太郎さんは、競技Xの日本人選手の2022年末時点でのベストタイムを調べた。その中で、2018年より前にベストタイムを出した選手と2018年以降にベストタイムを出した選手に分け、それぞれにおいて速い方から50人の選手のベストタイムをデータA,データBとした。
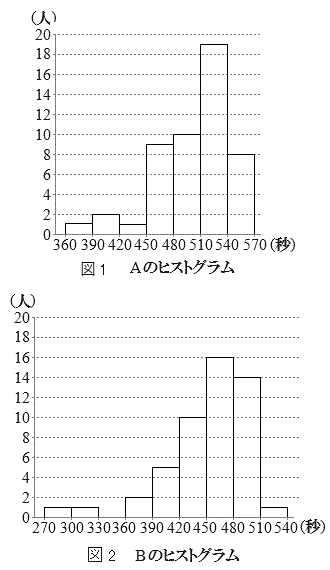 (i) 図1と図2はそれぞれ、階級の幅を30秒としたAとBのヒストグラムである。なお、ヒストグラムの各階級の区間は、左側の数値を含み、右側の数値を含まない。
(i) 図1と図2はそれぞれ、階級の幅を30秒としたAとBのヒストグラムである。なお、ヒストグラムの各階級の区間は、左側の数値を含み、右側の数値を含まない。図1からAの最頻値は階級 の階級値である。また、図2からBの中央値が含まれる階級は
の階級値である。また、図2からBの中央値が含まれる階級は である。
である。
 ,
, の解答群(同じものを繰り返し選んでもよい。)
の解答群(同じものを繰り返し選んでもよい。)  270以上300未満
270以上300未満  300以上330未満
300以上330未満
 330以上360未満
330以上360未満  360以上390未満
360以上390未満
 390以上420未満
390以上420未満  420以上450未満
420以上450未満
 450以上480未満
450以上480未満  480以上510未満
480以上510未満
 510以上540未満
510以上540未満  540以上570未満
540以上570未満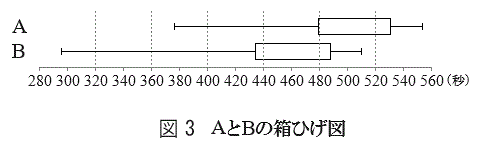 (ii) 図3は、A,Bそれぞれの箱ひげ図を並べたものである。ただし、中央値を示す線は省いている。
(ii) 図3は、A,Bそれぞれの箱ひげ図を並べたものである。ただし、中央値を示す線は省いている。
図3より次のことが読み取れる。ただし、A,Bそれぞれにおける、速い方から13番目の選手は一人ずつとする。
・Bの速い方から13番目の選手のベストタイムは、Aの速い方から13番目の選手のベストタイムより、およそ 秒速い。
秒速い。 ・Aの四分位範囲からBの四分位範囲を引いた差の絶対値は である。
である。  については、最も適当なものを、次の
については、最も適当なものを、次の ~
~ のうちから一つ選べ。
のうちから一つ選べ。 の解答群
の解答群 0以上20未満
0以上20未満 20以上40未満
20以上40未満 40以上60未満
40以上60未満 60以上80未満
60以上80未満 80以上100未満
80以上100未満(iii) 太郎さんは、Aのある選手とBのある選手のベストタイムの比較において、その二人の選手のベストタイムが速いか遅いかとは別の観点でも考えるために、次の式を満たすzの値を用いて判断することにした。
-式--------------
(あるデータのある選手のベストタイム)=
(そのデータの平均値)+z×(そのデータの標準偏差)
----------------
二人の選手それぞれのベストタイムに対するzの値を比較し、その値の小さい選手の方が優れていると判断する。
表1は、A,Bそれぞれにおける、速い方から1番目の選手(以下、1位の選手)のベストタイムと、データの平均値と標準偏差をまとめたものである。
表1 1位選手のベストタイム、平均値、標準偏差
| データ | 1位の選手のベストタイム | 平均値 | 標準偏差 |
| A | 376 | 504 | 40 |
| B | 296 | 454 | 45 |
式と表1を用いると、Bの1位の選手に対するベストタイムに対するzの値はである。このことから、Bの1位の選手のベストタイムは、平均値より標準偏差のおよそ 倍だけ小さいことがわかる。A,Bそれぞれにおける、1位の選手についての記述として、次の
倍だけ小さいことがわかる。A,Bそれぞれにおける、1位の選手についての記述として、次の ~
~ のうち、正しいものは
のうち、正しいものは である。
である。
 の解答群
の解答群  ベストタイムで比較するとAの1位の選手の方が速く、zの値で比較するとAの1位の選手の方が優れている。
ベストタイムで比較するとAの1位の選手の方が速く、zの値で比較するとAの1位の選手の方が優れている。 ベストタイムで比較するとBの1位の選手の方が速く、zの値で比較するとBの1位の選手の方が優れている。
ベストタイムで比較するとBの1位の選手の方が速く、zの値で比較するとBの1位の選手の方が優れている。 ベストタイムで比較するとAの1位の選手の方が速く、zの値で比較するとBの1位の選手の方が優れている。
ベストタイムで比較するとAの1位の選手の方が速く、zの値で比較するとBの1位の選手の方が優れている。 ベストタイムで比較するとBの1位の選手の方が速く、zの値で比較するとAの1位の選手の方が優れている。
ベストタイムで比較するとBの1位の選手の方が速く、zの値で比較するとAの1位の選手の方が優れている。(2) 太郎さんは、競技X,競技Y,競技Zのベストタイムに関連がないかを調べることにした。そのために、2022年末時点でのこれら3種目のベストタイムをすべて確認できた日本人男子選手のうち、競技Xのベストタイムが速い方から50人を選んだ。
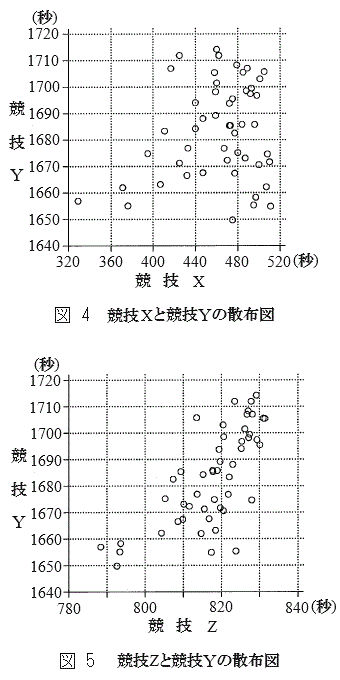 図4と図5はそれぞれ、選んだ50人についての競技Xと競技Yのベストタイム、競技Zと競技Yのベストタイムの散布図である。ただし、なお、これらの散布図には、完全に重なっている点はない。
図4と図5はそれぞれ、選んだ50人についての競技Xと競技Yのベストタイム、競技Zと競技Yのベストタイムの散布図である。ただし、なお、これらの散布図には、完全に重なっている点はない。
次の(a),(b)は、図4と図5に関する記述である。
(a) 競技Xのベストタイムの速い方から3番目までの選手の競技Yのベストタイムは、3選手とも1670秒未満である。
(b) 競技Xと競技Yの間の相関は、競技Zと競技Yの間の相関より強い。
(a),(b)の正誤の組み合わせとして正しいものは である。
である。
 の解答群
の解答群 注.共通テストの実際の問題文は、当塾とは無関係の私的企業の私的サイトから作問しているように書かれているため、著作権法上、本ウェブサイトにそのまま掲載することができません。問題文を大幅に改変したため、わかりづらくなっていることお詫び申し上げます。 [解答へ]
[3] 箱の中にカードが2枚以上入っており、それぞれのカードにはアルファベットが1文字だけ書かれている。この箱の中からカードを1枚取り出し、書かれているアルファベットを確認してからもとに戻すという試行を繰り返し行う。
(1) 箱の中に ,
, のカードが1枚ずつ全部で2枚入っている場合を考える。
のカードが1枚ずつ全部で2枚入っている場合を考える。 以下では、2以上の自然数nに対し、n回の試行でA,Bがそろっているとは、n回の試行で ,
, のそれぞれが少なくとも1回は取り出されることを意味する。
のそれぞれが少なくとも1回は取り出されることを意味する。 (i) 2回の試行でA,Bがそろっている確率は である。
である。 (ii) 3回の試行でA,Bがそろっている確率を求める。
例えば、3回の試行のうち を1回、
を1回、 を2回取り出す取り出し方は3通りあり、それらをすべて挙げると次のようになる。このように考えることにより、3回の試行でA,Bがそろっている取り出し方は
を2回取り出す取り出し方は3通りあり、それらをすべて挙げると次のようになる。このように考えることにより、3回の試行でA,Bがそろっている取り出し方は 通りあることがわかる。よって、3回の試行でA,Bがそろっている確率は
通りあることがわかる。よって、3回の試行でA,Bがそろっている確率は である。
である。 (iii) 4回の試行でA,Bがそろっている取り出し方は 通りある。よって、4回の試行でA,Bがそろっている確率は
通りある。よって、4回の試行でA,Bがそろっている確率は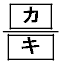 である。
である。
(2) 箱の中に ,
, ,
, のカードが1枚ずつ全部で3枚入っている場合を考える。
のカードが1枚ずつ全部で3枚入っている場合を考える。 以下では、3以上の自然数nに対し、n回目の試行で初めてA,B,Cがそろうとは、n回の試行で ,
, ,
, のそれぞれが少なくとも1回は取り出され、かつ
のそれぞれが少なくとも1回は取り出され、かつ ,
, ,
, のうちいずれか1枚がn回目の試行で初めて取り出されることを意味する。
のうちいずれか1枚がn回目の試行で初めて取り出されることを意味する。 (i) 3回目の試行で初めてA,B,Cがそろう取り出し方は 通りある。よって、3回目の試行で初めてA,B,Cがそろう確率は
通りある。よって、3回目の試行で初めてA,B,Cがそろう確率は である。
である。 (ii) 4回目の試行で初めてA,B,Cがそろう確率を求める。
4回目の試行で初めてA,B,Cがそろう取り出し方は、(1)の(ii)を振り返ることにより、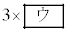 通りあることがわかる。よって、4回目の試行で初めてA,B,Cがそろう確率は
通りあることがわかる。よって、4回目の試行で初めてA,B,Cがそろう確率は である。
である。 (iii) 5回目の試行で初めてA,B,Cがそろう取り出し方は 通りある。よって、5回目の試行で初めてA,B,Cがそろう確率は
通りある。よって、5回目の試行で初めてA,B,Cがそろう確率は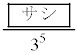 である。
である。
(3) 箱の中に ,
, ,
, ,
, のカードが1枚ずつ全部で4枚入っている場合を考える。
のカードが1枚ずつ全部で4枚入っている場合を考える。 以下では、6回目の試行で初めてA,B,C,Dがそろうとは、6回の試行で ,
, ,
, ,
, のそれぞれが少なくとも1回は取り出され、かつ
のそれぞれが少なくとも1回は取り出され、かつ ,
, ,
, ,
, のうちいずれか1枚が6回目の試行で初めて取り出されることを意味する。
のうちいずれか1枚が6回目の試行で初めて取り出されることを意味する。
また、3以上5以下の自然数nに対し、6回の試行のうちn回目の試行で初めてA,B,Cだけがそろうとは、6回の試行のうち1回目からn回目の試行で、 ,
, ,
, のそれぞれが少なくとも1回は取り出され、
のそれぞれが少なくとも1回は取り出され、 は1回も取り出されず、かつ
は1回も取り出されず、かつ ,
, ,
, のうちいずれか1枚がn回目の試行で初めて取り出されることを意味する。6回の試行のうちn回目の試行で初めてB,C,Dだけがそろうなども同様に定める。
のうちいずれか1枚がn回目の試行で初めて取り出されることを意味する。6回の試行のうちn回目の試行で初めてB,C,Dだけがそろうなども同様に定める。
太郎さんと花子さんは、6回目の試行で初めてA,B,C,Dがそろう確率について考えている。
太郎:例えば、5回目までに ,
, ,
, のそれぞれが少なくとも1回は取り出され、かつ6回目に初めて
のそれぞれが少なくとも1回は取り出され、かつ6回目に初めて が取り出さる場合を考えたら計算できそうだね。
が取り出さる場合を考えたら計算できそうだね。 花子:それなら、初めてA,B,Cだけがそろうのが、3回目のとき、4回目のとき、5回目のときで分けて考えてみてはどうかな。
[解答へ]
[4] T3,T4,T6を次のようなタイマーとする。
T3:3進数を3桁表示するタイマー
T4:4進数を3桁表示するタイマー
T6:6進数を3桁表示するタイマー
なお、n進数とはn進法で表された数のことである。
これらのタイマーは、すべて次の表示方法に従うものとする。
-表示方法-----------
(a) スタートした時点でタイマーは000と表示されている。
(b) タイマーは、スタートした後、表示される数が1秒ごとに1ずつ増えていき、3桁で表示できる最大の数が表示された1秒後に、表示が000に戻る。
(c) タイマーは表示が000に戻った後も、(b)と同様に、表示される数が1秒ごとに1ずつ増えていき、3桁で表示できる最大の数が表示された1秒後に、表示が000に戻るという動作を繰り返す。
----------------
例えば、T3はスタートしてから3進数で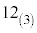 秒後に012と表示される。その後、222と表示された1秒後に表示が000に戻り、その
秒後に012と表示される。その後、222と表示された1秒後に表示が000に戻り、その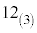 秒後に再び012と表示される。
秒後に再び012と表示される。
(1) T6は、スタートしてから10進数で40秒後に と表示される。
と表示される。 T4は、スタートしてから2進数で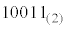 秒後に
秒後に と表示される。
と表示される。
(2) T4をスタートさせた後、初めて表示が000に戻るのは、スタートしてから10進数で 秒後であり、その後も
秒後であり、その後も 秒ごとに表示が000に戻る。
秒ごとに表示が000に戻る。 同様の考察をT6に対しても行うことにより、T4とT6を同時にスタートさせた後、初めて両方の表示が同時に000に戻るのは、スタートしてから10進数で 秒後であることがわかる。
秒後であることがわかる。
(3) 0以上の整数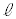 に対して、T4をスタートさせた
に対して、T4をスタートさせた 秒後にT4が012と表示されることと
秒後にT4が012と表示されることと は同値である。ただし、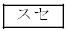 と
と は10進法で表されているものとする。T3についても同様の考察を行うことにより、次のことがわかる。T3とT4を同時にスタートさせてから、初めて両方が012と表示されるまでの時間をm秒とするとき、mは10進数で
は10進法で表されているものとする。T3についても同様の考察を行うことにより、次のことがわかる。T3とT4を同時にスタートさせてから、初めて両方が012と表示されるまでの時間をm秒とするとき、mは10進数で と表される。
と表される。
また、T4とT6の表示に関する記述として、次の ~
~ のうち、正しいものは
のうち、正しいものは である。
である。
 の解答群
の解答群 T4とT6を同時にスタートさせてから、m秒後より前に初めて両方が同時に012と表示される。
T4とT6を同時にスタートさせてから、m秒後より前に初めて両方が同時に012と表示される。 T4とT6を同時にスタートさせてから、ちょうどm秒後に初めて両方が同時に012と表示される。
T4とT6を同時にスタートさせてから、ちょうどm秒後に初めて両方が同時に012と表示される。 T4とT6を同時にスタートさせてから、m秒後より後に初めて両方が同時に012と表示される。
T4とT6を同時にスタートさせてから、m秒後より後に初めて両方が同時に012と表示される。 T4とT6を同時にスタートさせてから、両方が同時に012と表示されることはない。
T4とT6を同時にスタートさせてから、両方が同時に012と表示されることはない。
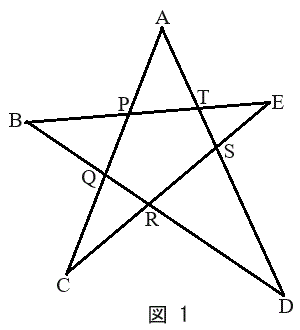 [5] 図1のように、平面上に5点A,B,C,D,Eがあり、線分AC,CE,EB,BD,DAによって、星形の図形ができるときを考える。線分ACとBEの交点をP,ACとBDの交点をQ,BDとCEの交点をR,ADとCEの交点をS,ADとBEの交点をTとする。
[5] 図1のように、平面上に5点A,B,C,D,Eがあり、線分AC,CE,EB,BD,DAによって、星形の図形ができるときを考える。線分ACとBEの交点をP,ACとBDの交点をQ,BDとCEの交点をR,ADとCEの交点をS,ADとBEの交点をTとする。
AP:PQ:QC = 2:3:3,AT:TS:SD = 1:1:3
を満たす星形の図形を考える。
以下の問題において比を解答する場合は、最も簡単な整数の比で答えよ。
(1) △AQDと直線CEに着目すると
が成り立つので
QR:RD =  :
:
となる。また、△AQDと直線BEに着目すると
QB:BD =  :
:
となる。したがって
となることがわかる。
(2) 5点P,Q,R,S,Tが同一円周上にあるとし、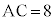 であるとする。
であるとする。 (i) 5点A,P,Q,S,Tに着目すると、AT:AS = 1:2より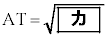 となる。さらに、5点D,Q,R,S,Tに着目すると
となる。さらに、5点D,Q,R,S,Tに着目すると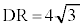 となることがわかる。
となることがわかる。 (ii) 3点A,B,Cを通る円と点Dとの位置関係を、次の構想に基づいて調べよう。
-構想-------------
線分ACとBDの交点Qに着目し、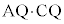 と
と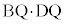 の大小を比べる。
の大小を比べる。 ----------------
まず、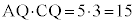 かつ
かつ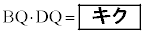 であることから
であることから 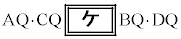 ・・・①
・・・①が成り立つ。また、3点A,B,Cを通る円と直線BDとの交点のうち、Bと異なる点をXとすると
 ・・・②
・・・②が成り立つ。①と②の左辺は同じなので、①と②の右辺を比べることにより、 が得られる。したがって、点Dは3点A,B,Cを通る円の
が得られる。したがって、点Dは3点A,B,Cを通る円の にある。
にある。
 ~
~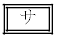 の解答群(同じものを繰り返し選んでもよい。)
の解答群(同じものを繰り返し選んでもよい。) <
<  =
=  >
>
 の解答群
の解答群
 内部
内部  周上
周上  外部
外部
(iii) 3点C,D,Eを通る円と2点A,Bとの位置関係について調べよう。
この星形の図形において、さらに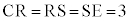 となることがわかる。したがって、点Aは3点C,D,Eを通る円の
となることがわかる。したがって、点Aは3点C,D,Eを通る円の にあり、点Bは3点C,D,Eを通る円の
にあり、点Bは3点C,D,Eを通る円の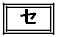 にある。
にある。
 ,
,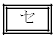 の解答群(同じものを繰り返し選んでもよい。)
の解答群(同じものを繰り返し選んでもよい。) 内部
内部  周上
周上  外部
外部 [解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。  ・・・④
・・・④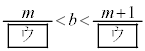
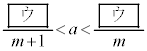 ・・・⑥
・・・⑥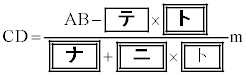
 である。
である。 である。
である。 である。
である。 である。
である。 である。
である。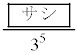 である。
である。 であることがわかる。
であることがわかる。