�@�Z���^�[���wIIB '08�N��1��@
[1]�@����x�Cy�́A
�@�@�@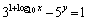 �@���(��)�����Ă���B���̂Ƃ�
�@���(��)�����Ă���B���̂Ƃ�
�@�@�@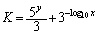
�̍ŏ��l�����߂悤�B
�^���̏����ɂ��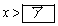 �ł���B�������A�ΐ�
�ł���B�������A�ΐ�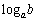 �ɑ��Aa���Ƃ����Ab��^���Ƃ����B���ɁA(��)�ɂ��
�ɑ��Aa���Ƃ����Ab��^���Ƃ����B���ɁA(��)�ɂ��
�@�@�@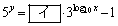
�ł���B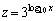 �Ƃ����ƁA
�Ƃ����ƁA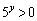 �ł��邩��Az�̂Ƃ蓾��l�͈̔͂�
�ł��邩��Az�̂Ƃ蓾��l�͈̔͂�
�@�@�@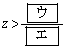
�ƂȂ�B�����
�@�@�@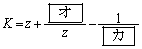
�ƂȂ邩��AK��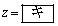 �̂Ƃ��A�ŏ��l
�̂Ƃ��A�ŏ��l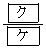 ���Ƃ�B���̂Ƃ��A
���Ƃ�B���̂Ƃ��A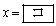 �C
�C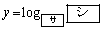 �ł���B
�ł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�^���������A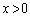 �@(�ΐ������Q��)
�@(�ΐ������Q��)
(�A) 0�@......[��]
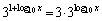 ��(��)���A
��(��)���A
(�C) 3�@......[��]
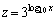 �Ƃ����ƁA
�Ƃ����ƁA
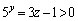 �@����@
�@����@
(�E) 1�@(�G) 3�@......[��]
(�I) 1�@(�J) 3�@......[��]
z�͐�������A�������ρE���敽�ς̊W���A
�s�����̓����́A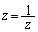 �܂�
�܂�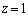 (
(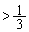 )�̂Ƃ��ɐ��藧���܂��B
)�̂Ƃ��ɐ��藧���܂��B
(�L) 1�@(�N) 5�@(�P) 3�@......[��]
���̂Ƃ��A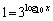 ���A
���A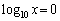 ������A
������A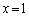
(�R) 1�@......[��]
�@���A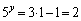
�ꂪ5�̑ΐ����Ƃ��āA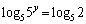
�� 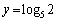
(�T) 5�@(�V) 2�@......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
[2]�@a�𐳂̒萔�Ƃ���B�_O�����_�Ƃ�����W���ʂɂ����āA���S��O�ŁA���a��1�̉~�Ɣ��a2�̉~�����ꂼ��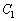 �C
�C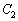 �Ƃ���B
�Ƃ���B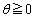 ��������θ �ɑ��āA�p
��������θ �ɑ��āA�p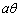 �̓��a��
�̓��a��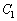 �Ƃ̌�_��P�Ƃ��A�p
�Ƃ̌�_��P�Ƃ��A�p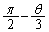 �̓��a��
�̓��a��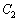 �Ƃ̌�_��Q�Ƃ���B�����ŁA���a��O�𒆐S�Ƃ��A���̎n����x���̐��̕����Ƃ���B
�Ƃ̌�_��Q�Ƃ���B�����ŁA���a��O�𒆐S�Ƃ��A���̎n����x���̐��̕����Ƃ���B
(1) 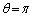 �̂Ƃ��AQ�̍��W��
�̂Ƃ��AQ�̍��W��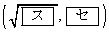 �ł���B
�ł���B
(2) 3�_O�CP�CQ�����̏��Ɉ꒼����ɂ���悤�ȍŏ���θ �̒l��
�@�@�@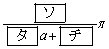
�ł���Bθ ��
�@�@�@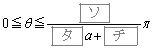
�͈̔͂��Ƃ��A�~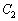 �ɂ����ē_Q�̋O�Ղ��ʂƂ����`�̖ʐς�
�ɂ����ē_Q�̋O�Ղ��ʂƂ����`�̖ʐς�
�@�@�@
�ł���B (3) ����PQ�̒�����2��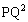 ��
�� �@�@�@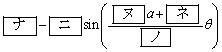
�ł���B (4) x�̊�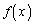 ��
�� �Ƃ����A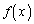 �̐��̎����̂����ŏ��̂��̂�
�̐��̎����̂����ŏ��̂��̂�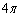 �ł���Ƃ���ƁA
�ł���Ƃ���ƁA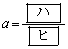 �ł���B
�ł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(3)�́A�]���藝��OK�ł����A�o��҂́A�O�p���Ōv�Z�����悤�Ƃ��Ă���悤�Ȃ̂ŁA�O�p���ł���Ă݂܂��B
�_P�́A���a1�̉~����̓_�ŁA���W�́A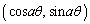 �C�_Q�́A���a2�̉~����̓_�ŁA���W�́A
�C�_Q�́A���a2�̉~����̓_�ŁA���W�́A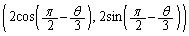 �ł��B
�ł��B
(1) 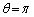 �̂Ƃ��AQ�̍��W�́A
�̂Ƃ��AQ�̍��W�́A (�X) 3�@(�Z) 1�@......[��]
(2) 3�_O�CP�CQ�����̏��Ɉ꒼����ɂ���ꍇ�A
(�\) 3�@(�^) 6�@(�`) 2�@......[��]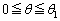 �̂Ƃ��A
�̂Ƃ��A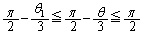 �Ȃ̂ŁA�~
�Ȃ̂ŁA�~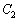 �ɂ����ē_Q�̋O�Ղ��ʂƂ����`�̒��p�́A
�ɂ����ē_Q�̋O�Ղ��ʂƂ����`�̒��p�́A ���̐�`�̖ʐς́A
(�c) 1�@(�e) 3�@(�g) 1�@......[��]
(3) 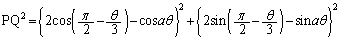
(�i) 5�@(�j) 4�@(�k) 3�@(�l) 1�@(�m) 3�@......[��]
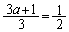 ��
�� 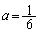
(�n) 1�@(�q) 6�@......[��]
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 
