�@��w���w���ʃe�X�g���wIIB 2023�N���@
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
[1][1]�@�O�p���̒l�̑召�W�ɂ��čl���悤�B
 �C
�C �̉Q(�������̂��J��Ԃ��I��ł��悢�B)
�̉Q(�������̂��J��Ԃ��I��ł��悢�B)
(2) 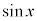 ��
��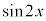 �̒l�̑召�W���ڂ������ׂ悤�B
�̒l�̑召�W���ڂ������ׂ悤�B �ł��邩��A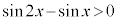 �����藧���Ƃ�
�����藧���Ƃ� �u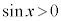 �@���@
�@���@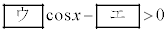 �v�@����@
�v�@����@ �܂���
�u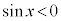 �@���@
�@���@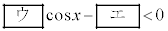 �v�@����A
�v�@����A �����藧���ƂƓ��l�ł���B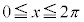 �̂Ƃ��A�@�����藧�悤��x�̒l�͈̔͂�
�̂Ƃ��A�@�����藧�悤��x�̒l�͈̔͂� �ł���A�A�����藧�悤��x�̒l�͈̔͂�
�ł���B����āA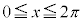 �̂Ƃ��A
�̂Ƃ��A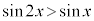 �����藧�悤��x�̒l�͈̔͂�
�����藧�悤��x�̒l�͈̔͂� 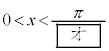 �C
�C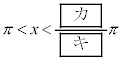
�ł���B
(3) 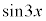 ��
��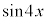 �̒l�̑召�W�ׂ悤�B
�̒l�̑召�W�ׂ悤�B �O�p���̉��@�藝��p����ƁA����
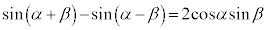 �@����B
�@����B��������B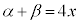 �C
�C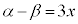 ����α�Cβ�ɑ��ćB��p���邱�Ƃɂ��A
����α�Cβ�ɑ��ćB��p���邱�Ƃɂ��A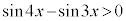 �����藧���Ƃ�
�����藧���Ƃ� �u �@���@
�@���@ �v�@����C
�v�@����C �܂���
�u �@���@
�@���@ �v�@����D
�v�@����D
�����藧���ƂƓ��l�ł��邱�Ƃ��킩��B
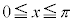 �̂Ƃ��A�C�C�D�ɂ��A
�̂Ƃ��A�C�C�D�ɂ��A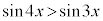 �����藧�悤��x�̒l�͈̔͂�
�����藧�悤��x�̒l�͈̔͂� 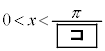 �C
�C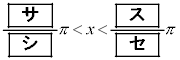
�ł���B
 �C
�C �̉Q(�������̂��J��Ԃ��I��ł��悢�B)
�̉Q(�������̂��J��Ԃ��I��ł��悢�B)  �@0�@�@
�@0�@�@ �@x�@�@
�@x�@�@ �@
�@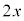 �@�@
�@�@ �@
�@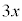
 �@
�@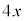 �@�@
�@�@ �@
�@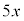 �@�@
�@�@ �@
�@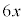 �@
�@ �@
�@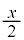
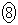 �@
�@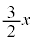 �@�@
�@�@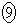 �@
�@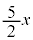 �@�@
�@�@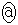 �@
�@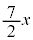 �@�@
�@�@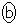 �@
�@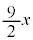
(4) (2)�C(3)�̍l�@����A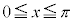 �̂Ƃ��A
�̂Ƃ��A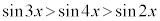 �����藧�悤��x�̒l�͈̔͂�
�����藧�悤��x�̒l�͈̔͂� 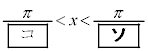 �C
�C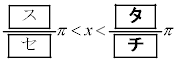
�ł��邱�Ƃ��킩��B
[2](1) 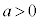 �C
�C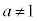 �C
�C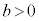 �̂Ƃ��A
�̂Ƃ��A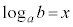 �Ƃ����ƁA
�Ƃ����ƁA �����藧�B
�����藧�B  �̉Q
�̉Q
(2) �l�X�ȑΐ��̒l���L���������������ɂ��čl���悤�B
(i) 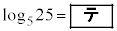 �C
�C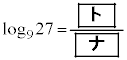 �ł���A�ǂ�����L�����ł���B
�ł���A�ǂ�����L�����ł���B
(ii) 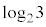 ���L�����Ɩ������̂ǂ���ł��邩���l���悤�B
���L�����Ɩ������̂ǂ���ł��邩���l���悤�B 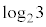 ���L�����ł���Ɖ��肷��ƁA
���L�����ł���Ɖ��肷��ƁA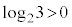 �ł���̂ŁA��̎��R��p�Cq��p����
�ł���̂ŁA��̎��R��p�Cq��p����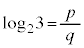 �ƕ\�����Ƃ��ł���B���̂Ƃ��A(1)�ɂ��
�ƕ\�����Ƃ��ł���B���̂Ƃ��A(1)�ɂ��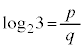 ��
�� �ƕό`�ł���B���܁A2�͋����ł���3�͊�ł���̂ŁA
�ƕό`�ł���B���܁A2�͋����ł���3�͊�ł���̂ŁA �������R��p�Cq�͑��݂��Ȃ��B
�������R��p�Cq�͑��݂��Ȃ��B
���������āA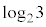 �͖��������Ƃ킩��B
�͖��������Ƃ킩��B
(iii) a�Cb��2�ȏ�̎��R���Ƃ���Ƃ��A(ii)�Ɠ��l�ɍl����ƁA�u �Ȃ��
�Ȃ��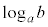 �͂˂ɖ������ł���v���Ƃ��킩��B
�͂˂ɖ������ł���v���Ƃ��킩��B  �̉Q
�̉Q �@
�@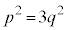 �@�@
�@�@ �@
�@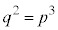 �@�@
�@�@ �@
�@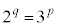
 �@
�@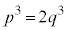 �@�@
�@�@ �@
�@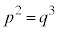 �@�@
�@�@ �@
�@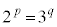
 �̉Q
�̉Q �@a������
�@a������
 �@b������
�@b������
 �@a���
�@a���
 �@b���
�@b���
 �@a��b���Ƃ��ɋ����A�܂���a��b���Ƃ��Ɋ
�@a��b���Ƃ��ɋ����A�܂���a��b���Ƃ��Ɋ
 �@a��b�̂����ꂩ����������ŁA����������
�@a��b�̂����ꂩ����������ŁA����������
[2][1](1) k�𐳂̒萔�Ƃ��A����3�������l����B
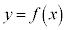 �̃O���t��x���Ƃ̋��L�_�̍��W��
�̃O���t��x���Ƃ̋��L�_�̍��W��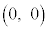 ��
�� �ł���B
�ł���B
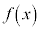 �̓���
�̓���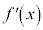 ��
���ł���B
 �̂Ƃ��A
�̂Ƃ��A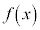 �͋ɏ��l
�͋ɏ��l ���Ƃ�B
���Ƃ�B
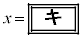 �̂Ƃ��A
�̂Ƃ��A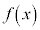 �͋ɑ�l
�͋ɑ�l ���Ƃ�B
���Ƃ�B
�܂��A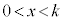 �͈̔͂ɂ�����
�͈̔͂ɂ�����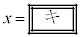 �̂Ƃ�
�̂Ƃ�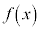 �͍ő�ƂȂ邱�Ƃ��킩��B
�͍ő�ƂȂ邱�Ƃ��킩��B
 �C
�C �`
�` �̉Q(�������̂��J��Ԃ��I��ł��悢�B)
�̉Q(�������̂��J��Ԃ��I��ł��悢�B)  �@0�@�@
�@0�@�@ �@
�@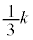 �@�@
�@�@ �@
�@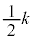 �@�@
�@�@ �@
�@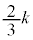
 �@k�@�@
�@k�@�@ �@
�@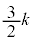 �@�@
�@�@ �@
�@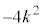 �@�@
�@�@ �@
�@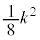
 �@
�@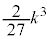 �@�@
�@�@ �@
�@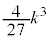 �@�@
�@�@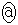 �@
�@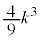 �@�@
�@�@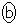 �@
�@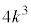
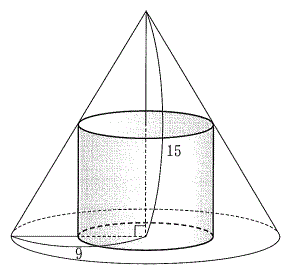 (2) �E�̐}�̂悤�ɒ�ʂ����a9�̉~�ō�����15�̉~���ɓ��ڂ���~�����l����B�~���̒�ʂ̔��a�Ƒ̐ς����ꂼ��x�CV�Ƃ���BV��x�̎��ŕ\����
(2) �E�̐}�̂悤�ɒ�ʂ����a9�̉~�ō�����15�̉~���ɓ��ڂ���~�����l����B�~���̒�ʂ̔��a�Ƒ̐ς����ꂼ��x�CV�Ƃ���BV��x�̎��ŕ\����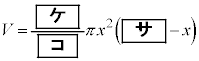 �@(
�@(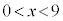 )
)�ł���B(1)�̍l�@���A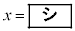 �̂Ƃ�V�͍ő�ƂȂ邱�Ƃ��킩��BV�̍ő�l��
�̂Ƃ�V�͍ő�ƂȂ邱�Ƃ��킩��BV�̍ő�l�� �ł���B
�ł���B
[2](1) ��ϕ�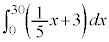 �̒l��
�̒l�� �ł���B
�ł���B �܂��A��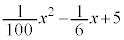 �̕s��ϕ���
�̕s��ϕ��� �ł���B�������AC�͐ϕ��萔�Ƃ���B
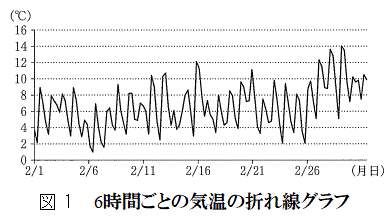 (2) ����n��ł́A���N3�����u�\���C���V�m(���̎��)�̊J�ԗ\�z���v���b��ɂȂ�B���Y����ƉԎq����́A�J�ԓ�����\�z������@�̈�ɁA2���ɓ����Ă���̋C�������Ԃ̊��Ƃ݂āA���̊���ϕ������l�����Ƃɂ�����@�����邱�Ƃ�m�����B�\���C���V�m�̊J�ԓ�����\�z���邽�߂ɁA��l�͐}1��6���Ԗ��̋C���̐܂�������Ȃ���A���̂悤�ɍl���邱�Ƃɂ����B
(2) ����n��ł́A���N3�����u�\���C���V�m(���̎��)�̊J�ԗ\�z���v���b��ɂȂ�B���Y����ƉԎq����́A�J�ԓ�����\�z������@�̈�ɁA2���ɓ����Ă���̋C�������Ԃ̊��Ƃ݂āA���̊���ϕ������l�����Ƃɂ�����@�����邱�Ƃ�m�����B�\���C���V�m�̊J�ԓ�����\�z���邽�߂ɁA��l�͐}1��6���Ԗ��̋C���̐܂�������Ȃ���A���̂悤�ɍl���邱�Ƃɂ����Bx�̒l�͈̔͂�0�ȏ�̎����S�̂Ƃ��āA2��1���ߑO0������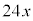 ���Ԍo�������_��x����Ƃ���B(�Ⴆ�A10.3�����2��11���ߑO7��12����\���B)�܂��Ax����̋C����y���Ƃ���B���̂Ƃ��Ay��x�̊��ł���A�����
���Ԍo�������_��x����Ƃ���B(�Ⴆ�A10.3�����2��11���ߑO7��12����\���B)�܂��Ax����̋C����y���Ƃ���B���̂Ƃ��Ay��x�̊��ł���A�����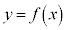 �Ƃ����B�������Ay�͕��ɂ͂Ȃ�Ȃ����̂Ƃ���B
�Ƃ����B�������Ay�͕��ɂ͂Ȃ�Ȃ����̂Ƃ���B
�C����\����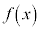 ��p���ē�l�̓\���C���V�m�̊J�ԓ����������ݒ��ōl���邱�Ƃɂ����B
��p���ē�l�̓\���C���V�m�̊J�ԓ����������ݒ��ōl���邱�Ƃɂ����B
�|�ݒ��|�|�|�|�|�|�|�|�|�|�|�|�|
���̎���t �ɑ��āA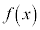 ��0����t �܂Őϕ������l��
��0����t �܂Őϕ������l��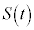 �Ƃ���B���Ȃ킿�A
�Ƃ���B���Ȃ킿�A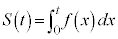 �Ƃ���B����
�Ƃ���B����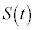 ��400�ɓ��B�����Ƃ��A�\���C���V�m���J�Ԃ���B
��400�ɓ��B�����Ƃ��A�\���C���V�m���J�Ԃ���B
�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|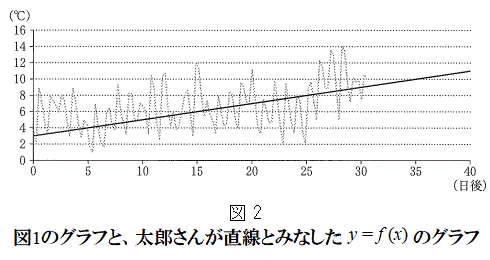 �ݒ��̂��ƁA���Y����͋C����\����
�ݒ��̂��ƁA���Y����͋C����\����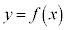 �̃O���t��}2�̂悤�ɒ����Ƃ݂Ȃ��ă\���C���V�m�̊J�ԓ������l���邱�Ƃɂ����B
�̃O���t��}2�̂悤�ɒ����Ƃ݂Ȃ��ă\���C���V�m�̊J�ԓ������l���邱�Ƃɂ����B (i) ���Y����́A
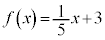 �@(
�@(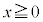 )
)�Ƃ��čl�����B���̂Ƃ��A�\���C���V�m�̊J�ԓ�����2���ɓ����Ă��� �ƂȂ�B
�ƂȂ�B
 �̉Q
�̉Q  �@30����@�@
�@30����@�@ �@35����@�@
�@35����@�@ �@40����
�@40����
 �@45����@�@
�@45����@�@ �@50����@�@
�@50����@�@ �@55����
�@55����
 �@60����@�@
�@60����@�@ �@65����
�@65����
(ii) ���Y����ƉԎq����́A2���ɓ����Ă���30����ȍ~�̋C���ɂ��Ęb�����Ă���B
�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|
���Y�F1������p���ă\���C���V�m�̊J�ԓ��������߂Ă݂���B
�Ԏq�F�C���̏オ�������l���āA2���ɓ����Ă���30����ȍ~�̋C����\������2�����̏ꍇ���l���Ă݂悤���B
�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|
�Ԏq����͋C����\����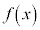 ���A
���A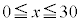 �̂Ƃ��͑��Y����Ɠ����悤��
�̂Ƃ��͑��Y����Ɠ����悤�� �Ƃ��A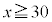 �̂Ƃ���
�̂Ƃ��� �Ƃ��čl�����B�Ȃ��A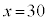 �̂Ƃ��@�̉E�ӂ̒l�ƇA�̉E�ӂ̒l�͈�v����B�Ԏq����̍l��������p���āA�\���C���V�m�̊J�ԓ������l���悤�B(1)���
�̂Ƃ��@�̉E�ӂ̒l�ƇA�̉E�ӂ̒l�͈�v����B�Ԏq����̍l��������p���āA�\���C���V�m�̊J�ԓ������l���悤�B(1)��� �ł���A
�ƂȂ邱�Ƃ��킩��B
�܂��A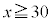 �͈̔͂ɂ�����
�͈̔͂ɂ�����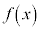 �͑�������B�����
�͑�������B����� �ł��邱�Ƃ��킩��B�ȏ���A�\���C���V�m�̊J�ԓ�����2���ɓ����Ă��� �ƂȂ�B
�ƂȂ�B
 �̉Q
�̉Q  �̉Q
�̉Q �@30������O
�@30������O
 �@30����
�@30����
 �@30�������A����40������O
�@30�������A����40������O
 �@40����
�@40����
 �@40�������A����50������O
�@40�������A����50������O
 �@50����
�@50����
 �@50�������A����60������O
�@50�������A����60������O
 �@60����
�@60����
 �@60�������
�@60�������
[3]�@�ȉ��̖�������ɂ������ẮA�K�v�ɉ�����43�y�[�W(���D�{�E�F�u�T�C�g�ł͖�蕶�̖���)�̐��K���z�\��p���Ă��悢�B
(1) ���鐶�Y�n�Ő��Y�����s�[�}���S�̂��W�c�Ƃ��A���̕�W�c�ɂ�����s�[�}��1�̏d��(�P�ʂ�g)��\���m���ϐ���X�Ƃ���Bm��σ�𐳂̎����Ƃ��AX�͐��K���z �ɏ]���Ƃ���B
�ɏ]���Ƃ���B
(i) ���̕�W�c����1�̃s�[�}����ׂɒ��o�����Ƃ��A�d����mg�ȏ�ł���m��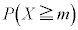 ��
�� �ł���B
(ii) ��W�c���疳��ׂɒ��o���ꂽ�傫��n�̕W�{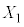 �C
�C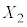 �C����C
�C����C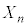 �̕W�{���ς�
�̕W�{���ς�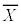 �Ƃ���B
�Ƃ���B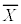 �̕���(���Ғl)�ƕW�����͂��ꂼ��
�̕���(���Ғl)�ƕW�����͂��ꂼ�� 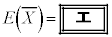 �C
�C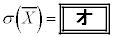
�ƂȂ�B
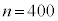 �C�W�{���ς�30.0g�C�W�{�̕W������3.6g�̂Ƃ��Am�̐M���x90���̐M����Ԃ��������j�ŋ��߂悤�B
�C�W�{���ς�30.0g�C�W�{�̕W������3.6g�̂Ƃ��Am�̐M���x90���̐M����Ԃ��������j�ŋ��߂悤�B
�|���j�|�|�|�|�|�|�|�|�|�|�|�|�|Z��W�����K���z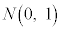 �ɏ]���m���ϐ��Ƃ��āA
�ɏ]���m���ϐ��Ƃ��āA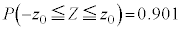 �ƂȂ�
�ƂȂ�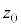 �𐳋K���z�\���狁�߂�B����
�𐳋K���z�\���狁�߂�B����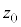 ��p�����m�̐M���x90.1���̐M����Ԃ����߂��邪�A�����M���x90���̐M����ԂƂ݂Ȃ��čl����B
��p�����m�̐M���x90.1���̐M����Ԃ����߂��邪�A�����M���x90���̐M����ԂƂ݂Ȃ��čl����B
�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|���j�ɂ����āA �ł���B
�ł���B
��ʂɁA�W�{�̑傫��n���傫���Ƃ��ɂ́A��W�����̑���ɁA�W�{�̕W������p���Ă悢���Ƃ��m����Ă���B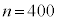 �͏\���ɑ傫���̂ŁA���j�Ɋ�Â��ƁAm�̐M���x90���̐M����Ԃ�
�͏\���ɑ傫���̂ŁA���j�Ɋ�Â��ƁAm�̐M���x90���̐M����Ԃ� �ƂȂ�B
�ƂȂ�B
 �C
�C �̉Q(�������̂��J��Ԃ��I��ł��悢�B)
�̉Q(�������̂��J��Ԃ��I��ł��悢�B)  �@σ�@�@
�@σ�@�@ �@
�@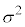 �@�@
�@�@ �@
�@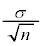 �@�@
�@�@ �@
�@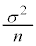
 �@m�@�@
�@m�@�@ �@
�@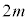 �@�@
�@�@ �@
�@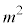 �@�@
�@�@ �@
�@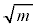
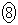 �@
�@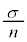 �@�@
�@�@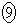 �@
�@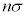 �@�@
�@�@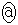 �@
�@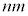 �@�@
�@�@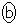 �@
�@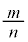
 �ɂ��ẮA�ł��K���Ȃ��̂��A����
�ɂ��ẮA�ł��K���Ȃ��̂��A���� �`
�` �̂��������I�ׁB
�̂��������I�ׁB �@
�@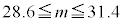 �@�@
�@�@ �@
�@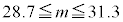 �@�@
�@�@ �@
�@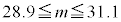
 �@
�@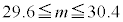 �@�@
�@�@ �@
�@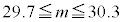 �@�@
�@�@ �@
�@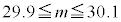
(2) (1)�̊m���ϐ�X�ɂ����āA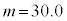 �C
�C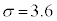 �Ƃ�����W�c���疳��ׂɃs�[�}����1�����o���A�s�[�}��2��1�g�ɂ������̂�܂ɓ���Ă����B���̂悤�ɂ��ăs�[�}��2��1�g�ɂ������̂�25�܍��B���̍ہA1�܂��̏d���̕��U�����������邽�߂ɁA�����s�[�}�����ޖ@���l����B
�Ƃ�����W�c���疳��ׂɃs�[�}����1�����o���A�s�[�}��2��1�g�ɂ������̂�܂ɓ���Ă����B���̂悤�ɂ��ăs�[�}��2��1�g�ɂ������̂�25�܍��B���̍ہA1�܂��̏d���̕��U�����������邽�߂ɁA�����s�[�}�����ޖ@���l����B
�|�s�[�}�����ޖ@�|�|�|�|�|�|�|�|
����ׂɒ��o�����������̃s�[�}���ɂ��āA�d����30.0g�ȉ��̂Ƃ���S�T�C�Y�A30.0g����Ƃ���L�T�C�Y�ƕ��ނ���B�����āA���ނ��ꂽ�s�[�}������S�T�C�Y��L�T�C�Y�̃s�[�}��������I�сA�s�[�}��2��1�g�Ƃ����܂����B
�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|
(i) �s�[�}����ׂ�50���o�����Ƃ��A�s�[�}�����ޖ@��25�܍�邱�Ƃ��ł���m��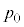 ���l���悤�B����ׂ�1���o�����s�[�}����S�T�C�Y�ł���m����
���l���悤�B����ׂ�1���o�����s�[�}����S�T�C�Y�ł���m����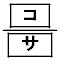 �ł���B�s�[�}����ׂ�50���o�����Ƃ���S�T�C�Y�̃s�[�}���̌���\���m���ϐ���
�ł���B�s�[�}����ׂ�50���o�����Ƃ���S�T�C�Y�̃s�[�}���̌���\���m���ϐ���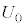 �Ƃ���ƁA
�Ƃ���ƁA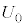 �͓��z
�͓��z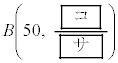 �ɏ]���̂�
�ɏ]���̂� �ƂȂ�B
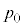 ���v�Z����ƁA
���v�Z����ƁA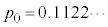 �ƂȂ邱�Ƃ���A�s�[�}����ׂ�50���o�����Ƃ��A25�܍�邱�Ƃ��ł���m����0.11���x�Ƃ킩��B
�ƂȂ邱�Ƃ���A�s�[�}����ׂ�50���o�����Ƃ��A25�܍�邱�Ƃ��ł���m����0.11���x�Ƃ킩��B
(ii) �s�[�}�����ޖ@��25�܍�邱�Ƃ��ł���m����0.95�ȏ�ƂȂ�悤�ȃs�[�}���̌����l���悤�B
k�����R���Ƃ��A�s�[�}����ׂ�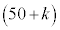 ���o�����Ƃ��AS�T�C�Y�̃s�[�}���̌���\���m���ϐ���
���o�����Ƃ��AS�T�C�Y�̃s�[�}���̌���\���m���ϐ���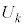 �Ƃ���ƁA
�Ƃ���ƁA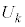 �͓��z
�͓��z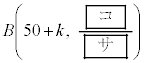 �ɏ]���B
�ɏ]���B
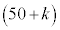 �͏\���ɑ傫���̂ŁA
�͏\���ɑ傫���̂ŁA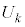 �͋ߎ��I�ɐ��K���z
�͋ߎ��I�ɐ��K���z �ɏ]���A
�ɏ]���A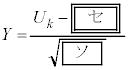 �Ƃ���ƁAY�͋ߎ��I�ɕW�����K���z
�Ƃ���ƁAY�͋ߎ��I�ɕW�����K���z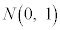 �ɏ]���B
�ɏ]���B
����āA�s�[�}�����ޖ@�ŁA25�܍�邱�Ƃ��ł���m����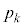 �Ƃ����
�Ƃ���� �ƂȂ�B
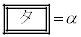 �C
�C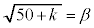 �Ƃ����B
�Ƃ����B
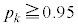 �ɂȂ�悤��
�ɂȂ�悤��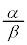 �ɂ��āA���K���z�\����
�ɂ��āA���K���z�\����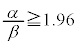 �����悢���Ƃ��킩��B�����ł�
�����悢���Ƃ��킩��B�����ł� 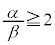 �@����@
�@����@�������R��k���l���邱�ƂƂ���B�@�̗��ӂ͐��ł��邩��A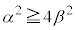 �����ŏ���k��
�����ŏ���k��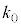 �Ƃ���ƁA
�Ƃ���ƁA �ł��邱�Ƃ��킩��B�������A
�ł��邱�Ƃ��킩��B�������A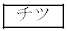 �̌v�Z�ɂ����ẮA
�̌v�Z�ɂ����ẮA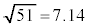 ��p���Ă��悢�B
��p���Ă��悢�B
���������āA���Ȃ��Ƃ� �̃s�[�}���𒊏o���Ă����A�s�[�}�����ޖ@��25�܍�邱�Ƃ��ł���m����0.95�ȏ�ƂȂ�B
�̃s�[�}���𒊏o���Ă����A�s�[�}�����ޖ@��25�܍�邱�Ƃ��ł���m����0.95�ȏ�ƂȂ�B
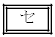 �`
�` �̉Q(�������̂��J��Ԃ��I��ł��悢�B)
�̉Q(�������̂��J��Ԃ��I��ł��悢�B)  �@k�@�@
�@k�@�@ �@
�@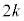 �@�@
�@�@ �@
�@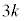 �@�@
�@�@ �@
�@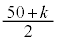
 �@
�@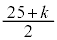 �@�@
�@�@ �@
�@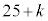 �@�@
�@�@ �@
�@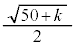 �@�@
�@�@ �@
�@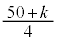
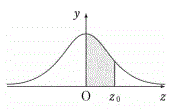
���K���z�\
���̕\�́A�W�����K���z�̕��z�Ȑ��ɂ�����E�}�D�F
�����̖ʐς��܂Ƃ߂����̂ł���B
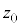 | 0.00 | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 |
| 0.0 | 0.0000 | 0.0040 | 0.0080 | 0.0120 | 0.0160 | 0.0199 | 0.0239 | 0.0279 | 0.0319 | 0.0359 |
| 0.1 | 0.0398 | 0.0438 | 0.0478 | 0.0517 | 0.0557 | 0.0596 | 0.0636 | 0.0675 | 0.0714 | 0.0753 |
| 0.2 | 0.0793 | 0.0832 | 0.0871 | 0.0910 | 0.0948 | 0.0987 | 0.1026 | 0.1064 | 0.1103 | 0.1141 |
| 0.3 | 0.1179 | 0.1217 | 0.1255 | 0.1293 | 0.1331 | 0.1368 | 0.1406 | 0.1443 | 0.1480 | 0.1517 |
| 0.4 | 0.1554 | 0.1591 | 0.1628 | 0.1664 | 0.1700 | 0.1736 | 0.1772 | 0.1808 | 0.1844 | 0.1879 |
| 0.5 | 0.1915 | 0.1950 | 0.1985 | 0.2019 | 0.2054 | 0.2088 | 0.2123 | 0.2157 | 0.2190 | 0.2224 |
| 0.6 | 0.2257 | 0.2291 | 0.2324 | 0.2357 | 0.2389 | 0.2422 | 0.2454 | 0.2486 | 0.2517 | 0.2549 |
| 0.7 | 0.2580 | 0.2611 | 0.2642 | 0.2673 | 0.2704 | 0.2734 | 0.2764 | 0.2794 | 0.2823 | 0.2852 |
| 0.8 | 0.2881 | 0.2910 | 0.2939 | 0.2967 | 0.2995 | 0.3023 | 0.3051 | 0.3078 | 0.3106 | 0.3133 |
| 0.9 | 0.3159 | 0.3186 | 0.3212 | 0.3238 | 0.3264 | 0.3289 | 0.3315 | 0.3340 | 0.3365 | 0.3389 |
| 1.0 | 0.3413 | 0.3438 | 0.3461 | 0.3485 | 0.3508 | 0.3531 | 0.3554 | 0.3577 | 0.3599 | 0.3621 |
| 1.1 | 0.3643 | 0.3665 | 0.3686 | 0.3708 | 0.3729 | 0.3749 | 0.3770 | 0.3790 | 0.3810 | 0.3830 |
| 1.2 | 0.3849 | 0.3869 | 0.3888 | 0.3907 | 0.3925 | 0.3944 | 0.3962 | 0.3980 | 0.3997 | 0.4015 |
| 1.3 | 0.4032 | 0.4049 | 0.4066 | 0.4082 | 0.4099 | 0.4115 | 0.4131 | 0.4147 | 0.4162 | 0.4177 |
| 1.4 | 0.4192 | 0.4207 | 0.4222 | 0.4236 | 0.4251 | 0.4265 | 0.4279 | 0.4292 | 0.4306 | 0.4319 |
| 1.5 | 0.4332 | 0.4345 | 0.4357 | 0.4370 | 0.4382 | 0.4394 | 0.4406 | 0.4418 | 0.4429 | 0.4441 |
| 1.6 | 0.4452 | 0.4463 | 0.4474 | 0.4484 | 0.4495 | 0.4505 | 0.4515 | 0.4525 | 0.4535 | 0.4545 |
| 1.7 | 0.4554 | 0.4564 | 0.4573 | 0.4582 | 0.4591 | 0.4599 | 0.4608 | 0.4616 | 0.4625 | 0.4633 |
| 1.8 | 0.4641 | 0.4649 | 0.4656 | 0.4664 | 0.4671 | 0.4678 | 0.4686 | 0.4693 | 0.4699 | 0.4706 |
| 1.9 | 0.4713 | 0.4719 | 0.4726 | 0.4732 | 0.4738 | 0.4744 | 0.4750 | 0.4756 | 0.4761 | 0.4767 |
| 2.0 | 0.4772 | 0.4778 | 0.4783 | 0.4788 | 0.4793 | 0.4798 | 0.4803 | 0.4808 | 0.4812 | 0.4817 |
| 2.1 | 0.4821 | 0.4826 | 0.4830 | 0.4834 | 0.4838 | 0.4842 | 0.4846 | 0.4850 | 0.4854 | 0.4857 |
| 2.2 | 0.4861 | 0.4864 | 0.4868 | 0.4871 | 0.4875 | 0.4878 | 0.4881 | 0.4884 | 0.4887 | 0.4890 |
| 2.3 | 0.4893 | 0.4896 | 0.4898 | 0.4901 | 0.4904 | 0.4906 | 0.4909 | 0.4911 | 0.4913 | 0.4916 |
| 2.4 | 0.4918 | 0.4920 | 0.4922 | 0.4925 | 0.4927 | 0.4929 | 0.4931 | 0.4932 | 0.4934 | 0.4936 |
| 2.5 | 0.4938 | 0.4940 | 0.4941 | 0.4943 | 0.4945 | 0.4946 | 0.4948 | 0.4949 | 0.4951 | 0.4952 |
| 2.6 | 0.4953 | 0.4955 | 0.4956 | 0.4957 | 0.4959 | 0.4960 | 0.4961 | 0.4962 | 0.4963 | 0.4964 |
| 2.7 | 0.4965 | 0.4966 | 0.4967 | 0.4968 | 0.4969 | 0.4970 | 0.4971 | 0.4972 | 0.4973 | 0.4974 |
| 2.8 | 0.4974 | 0.4975 | 0.4976 | 0.4977 | 0.4977 | 0.4978 | 0.4979 | 0.4979 | 0.4980 | 0.4981 |
| 2.9 | 0.4981 | 0.4982 | 0.4982 | 0.4983 | 0.4984 | 0.4984 | 0.4985 | 0.4985 | 0.4986 | 0.4986 |
| 3.0 | 0.4987 | 0.4987 | 0.4987 | 0.4988 | 0.4988 | 0.4989 | 0.4989 | 0.4989 | 0.4990 | 0.4990 |
[��]
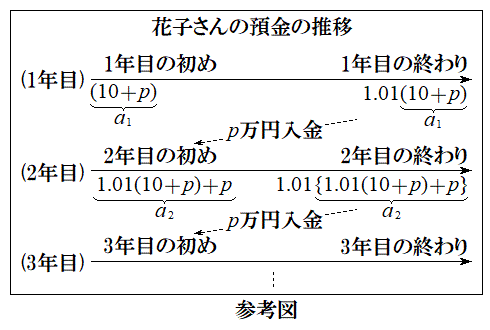 [4]�@�Ԏq����́A���N�̎n�߂ɗa�������Ɉ��z�̓��������邱�Ƃɂ����B���̓������n�߂�O�ɂ�����Ԏq����̗a����10���~�ł���B�����ŁA�a���Ƃ͗a�������ɂ��邨���̊z�̂��Ƃł���B�a���ɂ͔N��1%�ŗ��������A����N�̏��߂̗a����x���~�ł���A���̔N�̏I���ɂ͗a����
[4]�@�Ԏq����́A���N�̎n�߂ɗa�������Ɉ��z�̓��������邱�Ƃɂ����B���̓������n�߂�O�ɂ�����Ԏq����̗a����10���~�ł���B�����ŁA�a���Ƃ͗a�������ɂ��邨���̊z�̂��Ƃł���B�a���ɂ͔N��1%�ŗ��������A����N�̏��߂̗a����x���~�ł���A���̔N�̏I���ɂ͗a����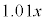 ���~�ƂȂ�B���̔N�̏��߂ɂ�
���~�ƂȂ�B���̔N�̏��߂ɂ�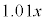 ���~�ɓ����z�����������̂��a���ƂȂ�B
���~�ɓ����z�����������̂��a���ƂȂ�B
���N���߂̓����z��p���~�Ƃ��An�N�ڂ̏��߂̗a����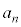 ���~�Ƃ����B�������A
���~�Ƃ����B�������A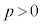 �Ƃ��An�͎��R���Ƃ���B
�Ƃ��An�͎��R���Ƃ���B
�Ⴆ�A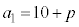 �C
�C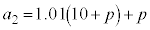 �ł���B
�ł���B
(1) 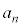 �����߂邽�߂ɓ�̕��j�ōl����B
�����߂邽�߂ɓ�̕��j�ōl����B �|���j�P�|�|�|�|�|�|�|�|�|�|�|�|n�N�ڂ̏��߂̗a����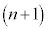 �N�ڂ̏��߂̗a���Ƃ̊W�ɒ��ڂ��čl����B
�N�ڂ̏��߂̗a���Ƃ̊W�ɒ��ڂ��čl����B
�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|3�N�ڂ̏��߂̗a��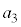 ���~�ɂ��āA
���~�ɂ��āA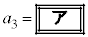 �ł���B���ׂĂ̎��R��n�ɂ���
�ł���B���ׂĂ̎��R��n�ɂ��� �����藧�B�����
�ƕό`�ł��A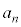 �����߂邱�Ƃ��ł���B
�����߂邱�Ƃ��ł���B
 �̉Q
�̉Q
 �`
�` �̉Q(�������̂��J��Ԃ��I��ł��悢�B)
�̉Q(�������̂��J��Ԃ��I��ł��悢�B)
 �@
�@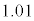 �@�@
�@�@ �@
�@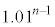 �@�@
�@�@ �@
�@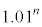
 �@p�@�@
�@p�@�@ �@
�@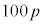 �@�@
�@�@ �@
�@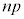
 �@
�@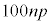 �@�@
�@�@ �@
�@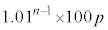 �@�@
�@�@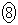 �@
�@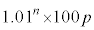
�|���j�Q�|�|�|�|�|�|�|�|�|�|�|�|
���Ƃ��Ɨa�������ɂ�����10���~�Ɩ��N�̏��߂ɓ�������p���~�ɂ��āAn�N�ڂ̏��߂ɂ��ꂼ�ꂪ������ɂȂ邩�ɒ��ڂ��čl����B
�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|
���Ƃ��Ɨa�������ɂ�����10���~�́A2�N�ڂ̏��߂ɂ�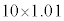 ���~�ɂȂ�A3�N�ڂ̏��߂ɂ�
���~�ɂȂ�A3�N�ڂ̏��߂ɂ�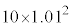 ���~�ɂȂ�B���l�ɍl�����n�N�ڂ̏��߂ɂ�
���~�ɂȂ�B���l�ɍl�����n�N�ڂ̏��߂ɂ�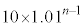 ���~�ɂȂ�B
���~�ɂȂ�B �E1�N�ڂ̏��߂ɓ�������p���~�́An�N�ڂ̏��߂ɂ�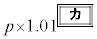 ���~�ɂȂ�B
���~�ɂȂ�B �E2�N�ڂ̏��߂ɓ�������p���~�́An�N�ڂ̏��߂ɂ�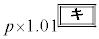 ���~�ɂȂ�B
���~�ɂȂ�B �En�N�ڂ̏��߂ɓ�������p���~�́An�N�ڂ̏��߂ɂ�p���~�̂܂܂ł���B
������
�ƂȂ邱�Ƃ��킩��B�����ŁA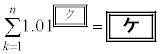 �ƂȂ�̂ŁA
�ƂȂ�̂ŁA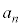 �����߂邱�Ƃ��ł���B
�����߂邱�Ƃ��ł���B
 �C
�C �̉Q(�������̂��J��Ԃ��I��ł��悢�B)
�̉Q(�������̂��J��Ԃ��I��ł��悢�B)  �̉Q
�̉Q �̉Q
�̉Q �@
�@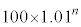 �@�@
�@�@ �@
�@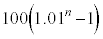
 �@
�@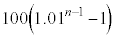 �@�@@3>>�@
�@�@@3>>�@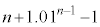
 �@
�@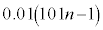 �@�@
�@�@ �@
�@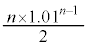
(2) �Ԏq����́A10�N�ڂ̏I���̗a����30���~�ȏ�ɂȂ邽�߂̓����z�ɂ��čl�����B
10�N�ڂ̏I���̗a����30���~�ȏ�ł��邱�Ƃ�s������p���ĕ\����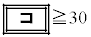 �ƂȂ�B���̕s������p�ɂ��ĉ�����
�ƂȂ�B���̕s������p�ɂ��ĉ����� �ƂȂ�B���������āA���N�̏��߂̓����z���Ⴆ��18000�~�ł���A10�N�ڂ̏I���̗a����30���~�ȏ�ɂȂ邱�Ƃ��킩��B
 �̉Q
�̉Q  �@
�@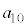 �@�@
�@�@ �@
�@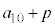 �@�@
�@�@ �@
�@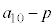
 �@
�@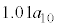 �@�@
�@�@ �@
�@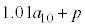 �@�@
�@�@ �@
�@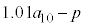
(3) 1�N�ڂ̓������n�߂�O�ɂ�����Ԏq����̗a����10���~�ł͂Ȃ��A13���~�̏ꍇ���l����B���ׂĂ̎��R��n�ɑ��āA���̏ꍇ��n�N�ڂ̏��߂̗a����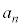 ���~����
���~���� ���~�����B�Ȃ��A�N����1���ł���A���N�̏��߂̓�����p���~�̂܂܂ł���B
���~�����B�Ȃ��A�N����1���ł���A���N�̏��߂̓�����p���~�̂܂܂ł���B  �̉Q
�̉Q �@3�@�@
�@3�@�@ �@13�@�@
�@13�@�@ �@
�@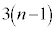
 �@
�@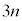 �@�@
�@�@ �@
�@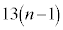 �@�@
�@�@ �@
�@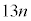
 �@
�@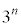 �@�@
�@�@ �@
�@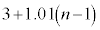 �@�@
�@�@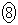 �@
�@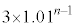
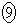 �@
�@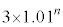 �@�@
�@�@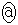 �@
�@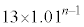 �@�@
�@�@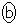 �@
�@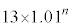
[��]
[5]�@�O�p��PABC�ɂ����āA��BC�̒��_��M�Ƃ����B�܂��A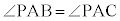 �Ƃ��A���̊p�x��θ�Ƃ����B�������A
�Ƃ��A���̊p�x��θ�Ƃ����B�������A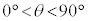 �Ƃ���B
�Ƃ���B
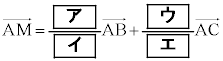
(1) 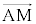 ��
�� �ƕ\����B�܂��A
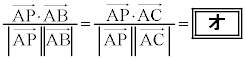 �@����@
�@����@�ł���B
 �̉Q
�̉Q  �@
�@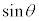 �@�@
�@�@ �@
�@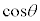 �@�@
�@�@ �@
�@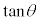
 �@
�@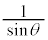 �@�@
�@�@ �@
�@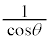 �@�@
�@�@ �@
�@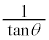
 �@
�@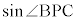 �@�@
�@�@ �@
�@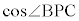 �@�@
�@�@ �@
�@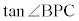
(2) 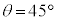 �Ƃ��A�����
�Ƃ��A����� �����藧�ꍇ���l����B���̂Ƃ�
�ł���B����ɁA����AM��̓_D��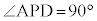 �����Ă���Ƃ���B���̂Ƃ��A
�����Ă���Ƃ���B���̂Ƃ��A �ł���B
�ł���B
(3) 
�Œ�܂�_��Q�Ƃ����B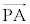 ��
��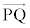 �������ł���O�p��PABC�͂ǂ̂悤�Ȃ��̂��ɂ��čl���悤�B�Ⴆ��(2)�̏ꍇ�ł́A�_Q�͓_D�ƈ�v���A
�������ł���O�p��PABC�͂ǂ̂悤�Ȃ��̂��ɂ��čl���悤�B�Ⴆ��(2)�̏ꍇ�ł́A�_Q�͓_D�ƈ�v���A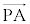 ��
��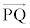 �͐����ł���B
�͐����ł���B
(i) 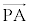 ��
��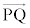 �������ł���Ƃ��A
�������ł���Ƃ��A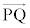 ��
��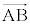 �C
�C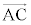 �C
�C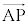 ��p���ĕ\���čl����ƁA
��p���ĕ\���čl����ƁA �����藧�B����ɇ@�ɒ��ӂ���ƁA
�����藧�B����ɇ@�ɒ��ӂ���ƁA ����
���� �����藧���Ƃ��킩��B
�����藧���Ƃ��킩��B ���������āA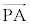 ��
��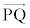 �������ł���A
�������ł���A �����藧�B�t��
�����藧�B�t�� �����藧�ĂA
�����藧�ĂA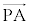 ��
��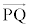 �͐����ł���B
�͐����ł���B
 �̉Q
�̉Q  �̉Q
�̉Q
(ii) k�𐳂̒萔�Ƃ�
�����藧�Ƃ���B���̂Ƃ��A �����藧�B
�����藧�B
�܂��A�_B���璼��AP�ɉ��낵�������ƒ���AP�Ƃ̌�_��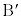 �Ƃ��A���l�ɓ_C���璼��AP�ɉ��낵�������ƒ���AP�Ƃ̌�_��
�Ƃ��A���l�ɓ_C���璼��AP�ɉ��낵�������ƒ���AP�Ƃ̌�_��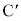 �Ƃ���B
�Ƃ���B
���̂Ƃ��A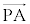 ��
��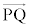 �������ł��邱�Ƃ́A
�������ł��邱�Ƃ́A �ł��邱�ƂƓ��l�ł���B����
�ł��邱�ƂƓ��l�ł���B����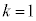 �̂Ƃ��A
�̂Ƃ��A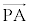 ��
��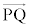 �������ł��邱�Ƃ́A
�������ł��邱�Ƃ́A �ł��邱�ƂƓ��l�ł���B
�ł��邱�ƂƓ��l�ł���B
 �̉Q
�̉Q  �̉Q
�̉Q �@
�@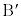 ��
��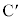 ������AP�����ꂼ��
������AP�����ꂼ��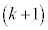 �F1��1�F
�F1��1�F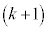 �ɓ�������_
�ɓ�������_ �@
�@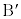 ��
��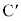 ������AP�����ꂼ��1�F
������AP�����ꂼ��1�F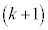 ��
��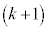 �F1�ɓ�������_
�F1�ɓ�������_ �@
�@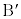 ��
��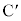 ������AP�����ꂼ��k�F1��1�Fk�ɓ�������_
������AP�����ꂼ��k�F1��1�Fk�ɓ�������_ �@
�@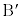 ��
��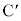 ������AP�����ꂼ��1�Fk��k�F1�ɓ�������_
������AP�����ꂼ��1�Fk��k�F1�ɓ�������_ �@
�@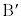 ��
��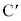 ���Ƃ��ɐ���AP��k�F1�ɓ�������_
���Ƃ��ɐ���AP��k�F1�ɓ�������_ �@
�@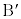 ��
��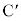 ���Ƃ��ɐ���AP��1�Fk�ɓ�������_
���Ƃ��ɐ���AP��1�Fk�ɓ�������_ �̉Q
�̉Q �@��PAB�Ɓ�PAC���Ƃ��ɐ��O�p�`
�@��PAB�Ɓ�PAC���Ƃ��ɐ��O�p�` �@��PAB�Ɓ�PAC�����ꂼ��
�@��PAB�Ɓ�PAC�����ꂼ��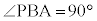 �C
�C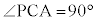 �������p�ӎO�p�`
�������p�ӎO�p�` �@��PAB�Ɓ�PAC�����ꂼ��
�@��PAB�Ɓ�PAC�����ꂼ��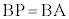 �C
�C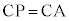 �����ӎO�p�`
�����ӎO�p�` �@��PAB�Ɓ�PAC������
�@��PAB�Ɓ�PAC������ �@
�@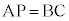
[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 
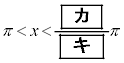
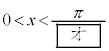 �C
�C
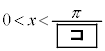 �C
�C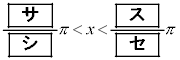
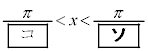 �C
�C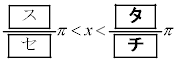
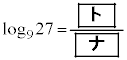 �ł���A�ǂ�����L�����ł���B
�ł���A�ǂ�����L�����ł���B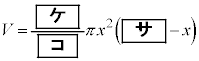 �@(
�@(
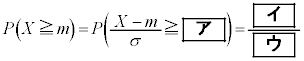
 �ł���B�s�[�}����ׂ�50���o�����Ƃ���S�T�C�Y�̃s�[�}���̌���\���m���ϐ���
�ł���B�s�[�}����ׂ�50���o�����Ƃ���S�T�C�Y�̃s�[�}���̌���\���m���ϐ��� �ɏ]���̂�
�ɏ]���̂�
 �ɏ]���B
�ɏ]���B �Ƃ���ƁAY�͋ߎ��I�ɕW�����K���z
�Ƃ���ƁAY�͋ߎ��I�ɕW�����K���z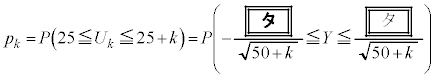
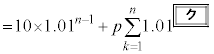
 �ƂȂ�̂ŁA
�ƂȂ�̂ŁA
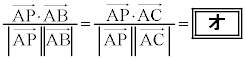 �@����@
�@����@