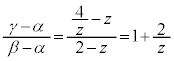大学入学共通テスト数学IIBC 2025年問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1](1) 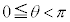 のとき、方程式
のとき、方程式 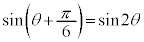 ・・・①
・・・①の解を求めよう。以下では、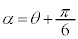 ,
,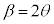 とおく。このとき、①は
とおく。このとき、①は 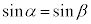 ・・・②
・・・②となる。
(i) 二つの一般角αとβが等しければ、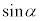 と
と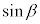 は等しい。
は等しい。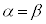 を満たすθは
を満たすθは であり、これは①の解の一つである。そして、
であり、これは①の解の一つである。そして、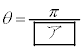 のとき
のとき となる。
(ii) 太郎さんと花子さんは、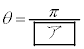 以外の①の解を求める方法について話している。
以外の①の解を求める方法について話している。
太郎:角が等しくなくても、サインの値が等しくなることがあるね。
花子:サインの値が等しくなるのはどんなときか、単位円を用いて考えてみようか。
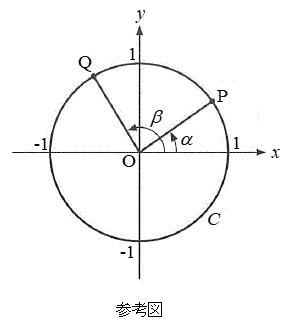 Oを原点とする座標平面において、中心がOで、半径が1の円をCとする。さらに、αの動径とCとの交点をP,βの動径とCとの交点をQとする。ここで、動径はOを中心とし、その始線はx軸の正の部分とする。
Oを原点とする座標平面において、中心がOで、半径が1の円をCとする。さらに、αの動径とCとの交点をP,βの動径とCとの交点をQとする。ここで、動径はOを中心とし、その始線はx軸の正の部分とする。
②が成り立つときに、点Pと点Qの間につねに成り立つ関係の記述として、次の ~
~ のうち、正しいものは
のうち、正しいものは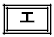 である。
である。
 の解答群
の解答群 点Pと点Qは同じ点である。
点Pと点Qは同じ点である。 点Pのx座標と、点Qのx座標が等しい。
点Pのx座標と、点Qのx座標が等しい。 点Pのy座標と、点Qのy座標が等しい。
点Pのy座標と、点Qのy座標が等しい。 点Pと点Qは、原点Oに関して対称である。
点Pと点Qは、原点Oに関して対称である。
(iii)  とする。
とする。 ・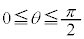 の場合を考える。このとき、
の場合を考える。このとき、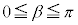 であるので、②が成り立つとき、(ii)で考察したことに注意すると、αとβは
であるので、②が成り立つとき、(ii)で考察したことに注意すると、αとβは を満たすことがわかる。これより、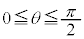 のときの①の解
のときの①の解 を得る。
・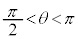 の場合を考える。このとき、
の場合を考える。このとき、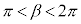 であるので、②が成り立つとき、(ii)で考察したことに注意すると、αとβは
であるので、②が成り立つとき、(ii)で考察したことに注意すると、αとβは を満たすことがわかる。これより、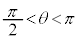 のときの①の解
のときの①の解 を得る。
以上より、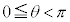 のとき、①の解は
のとき、①の解は である。
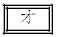 ,
, の解答群(同じものを繰り返し選んでもよい)
の解答群(同じものを繰り返し選んでもよい) 0
0 
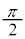
 π
π 
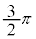

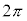

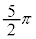

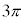

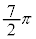
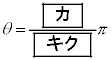
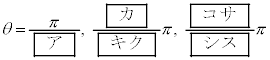
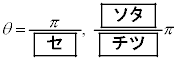
(2) 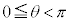 のとき、方程式
のとき、方程式 の解は
である。
[解答へ]
[2] 以下の問題を解答するにあたっては、必要に応じて問題末の常用対数表を用いてもよい。
学校の池でメダカを飼うことが決まり、メダカの飼育係になった花子さんは、水質を良くする効果がある水草Aを水面に浮かべることにした。一方で、水草Aが増えすぎてメダカに悪影響を与えることを心配した花子さんは、水草Aを定期的に除去することにし、その作業の計画を立てるために次の基本方針を定めた。
-基本方針---------------
・水草Aの量を水草Aが池の水面を覆う面積の割合(%)で測ることにし、この量をもとに作業計画を立てる。
・作業は正午に行う。
--------------------
(1) 水草Aの増え方を知るために、観測を行った。次の表は、観測を開始した日を0日目として、0日目、3日目、6日目、9日目の正午に観測した水草Aの量を表したものである。
| 観測日(日目) | 0 | 3 | 6 | 9 |
| 水草Aの量(%) | 17.2 | 22.7 | 30.0 | 39.6 |
>
水草Aの量が3日ごとに何倍に増えるのかを計算して小数第3位を四捨五入したところ、いずれも1.32倍であることがわかった。水草Aの量は、3日ごとにほとんど同じ倍率で増えていることから、「水草Aの量は、1日ごとに一定の倍率で増える」と考え、その倍率を定数rとした。
観測結果から、3日目の水草Aの量は0日目の量の1.32倍になると考えた。このとき、rは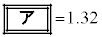 を満たす。
を満たす。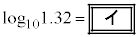 であるので
であるのでが得られる。
 の解答群
の解答群
 r
r 
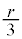

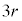

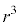

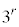

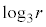
 の解答群
の解答群
 0.0899
0.0899  0.1206
0.1206  0.1523
0.1523  0.2148
0.2148  0.2405
0.2405  0.3010
0.3010  0.3636
0.3636  0.4771
0.4771
(2) 花子さんは、基本方針に次の条件を加えて、作業計画を立てることにした。
-条件----------------
・作業は14日ごとに行う。
・作業の後に残す水草Aの量を、次回の作業までの間に水草Aの量がつねに60%を超えない範囲で、できるだけ多くする。。
-------------------
作業の日に残す水草Aの量について考える。
作業を行った日を0日目として、次回の作業は14日目に行う、なお、作業にかかる時間は考えないものとする。
次のような実数aを考える。作業の後に残す水草Aの量をa%としたとき、14日目の正午に水草Aの量がちょうど60%になる。
このとき、(1)の定数rを用いると、14日目の正午に水草Aの量はaの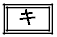 倍になるので
倍になるので 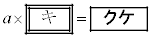 ・・・①
・・・①が成り立つ。
①の両辺の常用対数をとり、(1)で求めた と
と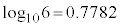 であることを用いると、
であることを用いると、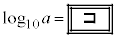 となる。aの決め方から、作業の後に残す水草Aの量をa%以下にすれば、次回の作業までの間に水草Aの量がつねに60%を超えないことがわかる。a以下で最大の整数は
となる。aの決め方から、作業の後に残す水草Aの量をa%以下にすれば、次回の作業までの間に水草Aの量がつねに60%を超えないことがわかる。a以下で最大の整数は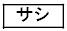 であることから、花子さんは作業の後に残す水草Aの量を
であることから、花子さんは作業の後に残す水草Aの量を %にすることにした。
%にすることにした。
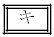 の解答群
の解答群
 r
r 
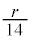

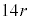

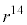

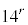

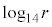
 については、最も適当なものを、次の
については、最も適当なものを、次の ~
~ のうちから一つ選べ。
のうちから一つ選べ。
 0.7758
0.7758  1.0670
1.0670  1.0934
1.0934  1.2154
1.2154  1.3410
1.3410  1.4894
1.4894  1.7806
1.7806  2.4666
2.4666
常用対数表
| 数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1.0 | 0.0000 | 0.0043 | 0.0086 | 0.0128 | 0.0170 | 0.0212 | 0.0253 | 0.0294 | 0.0334 | 0.0374 |
| 1.1 | 0.0414 | 0.0453 | 0.0492 | 0.0531 | 0.0569 | 0.0607 | 0.0645 | 0.0682 | 0.0719 | 0.0755 |
| 1.2 | 0.0792 | 0.0828 | 0.0864 | 0.0899 | 0.0934 | 0.0969 | 0.1004 | 0.1038 | 0.1072 | 0.1106 |
| 1.3 | 0.1139 | 0.1173 | 0.1206 | 0.1239 | 0.1271 | 0.1303 | 0.1335 | 0.1367 | 0.1399 | 0.1430 |
| 1.4 | 0.1461 | 0.1492 | 0.1523 | 0.1553 | 0.1584 | 0.1614 | 0.1644 | 0.1673 | 0.1703 | 0.1732 |
| 1.5 | 0.1761 | 0.1790 | 0.1818 | 0.1847 | 0.1875 | 0.1903 | 0.1931 | 0.1959 | 0.1987 | 0.2014 |
| 1.6 | 0.2041 | 0.2068 | 0.2095 | 0.2122 | 0.2148 | 0.2175 | 0.2201 | 0.2227 | 0.2253 | 0.2279 |
| 1.7 | 0.2304 | 0.2330 | 0.2355 | 0.2380 | 0.2405 | 0.2430 | 0.2455 | 0.2480 | 0.2504 | 0.2529 |
| 1.8 | 0.2553 | 0.2577 | 0.2601 | 0.2625 | 0.2648 | 0.2672 | 0.2695 | 0.2718 | 0.2742 | 0.2765 |
| 1.9 | 0.2788 | 0.2810 | 0.2833 | 0.2856 | 0.2878 | 0.2900 | 0.2923 | 0.2945 | 0.2967 | 0.2989 |
| 2.0 | 0.3010 | 0.3032 | 0.3054 | 0.3075 | 0.3096 | 0.3118 | 0.3139 | 0.3160 | 0.3181 | 0.3201 |
| 2.1 | 0.3222 | 0.3243 | 0.3263 | 0.3284 | 0.3304 | 0.3324 | 0.3345 | 0.3365 | 0.3385 | 0.3404 |
| 2.2 | 0.3424 | 0.3444 | 0.3464 | 0.3483 | 0.3502 | 0.3522 | 0.3541 | 0.3560 | 0.3579 | 0.3598 |
| 2.3 | 0.3617 | 0.3636 | 0.3655 | 0.3674 | 0.3692 | 0.3711 | 0.3729 | 0.3747 | 0.3766 | 0.3784 |
| 2.4 | 0.3802 | 0.3820 | 0.3838 | 0.3856 | 0.3874 | 0.3892 | 0.3909 | 0.3927 | 0.3945 | 0.3962 |
| 2.5 | 0.3979 | 0.3997 | 0.4014 | 0.4031 | 0.4048 | 0.4065 | 0.4082 | 0.4099 | 0.4116 | 0.4133 |
| 2.6 | 0.4150 | 0.4166 | 0.4183 | 0.4200 | 0.4216 | 0.4232 | 0.4249 | 0.4265 | 0.4281 | 0.4298 |
| 2.7 | 0.4314 | 0.4330 | 0.4346 | 0.4362 | 0.4378 | 0.4393 | 0.4409 | 0.4425 | 0.4440 | 0.4456 |
| 2.8 | 0.4472 | 0.4487 | 0.4502 | 0.4518 | 0.4533 | 0.4548 | 0.4564 | 0.4579 | 0.4594 | 0.4609 |
| 2.9 | 0.4624 | 0.4639 | 0.4654 | 0.4669 | 0.4683 | 0.4698 | 0.4713 | 0.4728 | 0.4742 | 0.4757 |
| 3.0 | 0.4771 | 0.4786 | 0.4800 | 0.4814 | 0.4829 | 0.4843 | 0.4857 | 0.4871 | 0.4886 | 0.4900 |
| 3.1 | 0.4914 | 0.4928 | 0.4942 | 0.4955 | 0.4969 | 0.4983 | 0.4997 | 0.5011 | 0.5024 | 0.5038 |
| 3.2 | 0.5051 | 0.5065 | 0.5079 | 0.5092 | 0.5105 | 0.5119 | 0.5132 | 0.5145 | 0.5159 | 0.5172 |
| 3.3 | 0.5185 | 0.5198 | 0.5211 | 0.5224 | 0.5237 | 0.5250 | 0.5263 | 0.5276 | 0.5289 | 0.5302 |
| 3.4 | 0.5315 | 0.5328 | 0.5340 | 0.5353 | 0.5366 | 0.5378 | 0.5391 | 0.5403 | 0.5416 | 0.5428 |
| 3.5 | 0.5441 | 0.5453 | 0.5465 | 0.5478 | 0.5490 | 0.5502 | 0.5514 | 0.5527 | 0.5539 | 0.5551 |
| 3.6 | 0.5563 | 0.5575 | 0.5587 | 0.5599 | 0.5611 | 0.5623 | 0.5635 | 0.5647 | 0.5658 | 0.5670 |
| 3.7 | 0.5682 | 0.5694 | 0.5705 | 0.5717 | 0.5729 | 0.5740 | 0.5752 | 0.5763 | 0.5775 | 0.5786 |
| 3.8 | 0.5798 | 0.5809 | 0.5821 | 0.5832 | 0.5843 | 0.5855 | 0.5866 | 0.5877 | 0.5888 | 0.5899 |
| 3.9 | 0.5911 | 0.5922 | 0.5933 | 0.5944 | 0.5955 | 0.5966 | 0.5977 | 0.5988 | 0.5999 | 0.6010 |
| 4.0 | 0.6021 | 0.6031 | 0.6042 | 0.6053 | 0.6064 | 0.6075 | 0.6085 | 0.6096 | 0.6107 | 0.6117 |
| 4.1 | 0.6128 | 0.6138 | 0.6149 | 0.6160 | 0.6170 | 0.6180 | 0.6191 | 0.6201 | 0.6212 | 0.6222 |
| 4.2 | 0.6232 | 0.6243 | 0.6253 | 0.6263 | 0.6274 | 0.6284 | 0.6294 | 0.6304 | 0.6314 | 0.6325 |
| 4.3 | 0.6335 | 0.6345 | 0.6355 | 0.6365 | 0.6375 | 0.6385 | 0.6395 | 0.6405 | 0.6415 | 0.6425 |
| 4.4 | 0.6435 | 0.6444 | 0.6454 | 0.6464 | 0.6474 | 0.6484 | 0.6493 | 0.6503 | 0.6513 | 0.6522 |
| 4.5 | 0.6532 | 0.6542 | 0.6551 | 0.6561 | 0.6571 | 0.6580 | 0.6590 | 0.6599 | 0.6609 | 0.6618 |
| 4.6 | 0.6628 | 0.6637 | 0.6646 | 0.6656 | 0.6665 | 0.6675 | 0.6684 | 0.6693 | 0.6702 | 0.6712 |
| 4.7 | 0.6721 | 0.6730 | 0.6739 | 0.6749 | 0.6758 | 0.6767 | 0.6776 | 0.6785 | 0.6794 | 0.6803 |
| 4.8 | 0.6812 | 0.6821 | 0.6830 | 0.6839 | 0.6848 | 0.6857 | 0.6866 | 0.6875 | 0.6884 | 0.6893 |
| 4.9 | 0.6902 | 0.6911 | 0.6920 | 0.6928 | 0.6937 | 0.6946 | 0.6955 | 0.6964 | 0.6972 | 0.6981 |
| 5.0 | 0.6990 | 0.6998 | 0.7007 | 0.7016 | 0.7024 | 0.7033 | 0.7042 | 0.7050 | 0.7059 | 0.7067 |
| 5.1 | 0.7076 | 0.7084 | 0.7093 | 0.7101 | 0.7110 | 0.7118 | 0.7126 | 0.7135 | 0.7143 | 0.7152 |
| 5.2 | 0.7160 | 0.7168 | 0.7177 | 0.7185 | 0.7193 | 0.7202 | 0.7210 | 0.7218 | 0.7226 | 0.7235 |
| 5.3 | 0.7243 | 0.7251 | 0.7259 | 0.7267 | 0.7275 | 0.7284 | 0.7292 | 0.7300 | 0.7308 | 0.7316 |
| 5.4 | 0.7324 | 0.7332 | 0.7340 | 0.7348 | 0.7356 | 0.7364 | 0.7372 | 0.7380 | 0.7388 | 0.7396 |
| 5.5 | 0.7404 | 0.7412 | 0.7419 | 0.7427 | 0.7435 | 0.7443 | 0.7451 | 0.7459 | 0.7466 | 0.7474 |
| 5.6 | 0.7482 | 0.7490 | 0.7497 | 0.7505 | 0.7513 | 0.7520 | 0.7528 | 0.7536 | 0.7543 | 0.7551 |
| 5.7 | 0.7559 | 0.7566 | 0.7574 | 0.7582 | 0.7589 | 0.7597 | 0.7604 | 0.7612 | 0.7619 | 0.7627 |
| 5.8 | 0.7634 | 0.7642 | 0.7649 | 0.7657 | 0.7664 | 0.7672 | 0.7679 | 0.7686 | 0.7694 | 0.7701 |
| 5.9 | 0.7709 | 0.7716 | 0.7723 | 0.7731 | 0.7738 | 0.7745 | 0.7752 | 0.7760 | 0.7767 | 0.7774 |
| 6.0 | 0.7782 | 0.7789 | 0.7796 | 0.7803 | 0.7810 | 0.7818 | 0.7825 | 0.7832 | 0.7839 | 0.7846 |
| 6.1 | 0.7853 | 0.7860 | 0.7868 | 0.7875 | 0.7882 | 0.7889 | 0.7896 | 0.7903 | 0.7910 | 0.7917 |
| 6.2 | 0.7924 | 0.7931 | 0.7938 | 0.7945 | 0.7952 | 0.7959 | 0.7966 | 0.7973 | 0.7980 | 0.7987 |
| 6.3 | 0.7993 | 0.8000 | 0.8007 | 0.8014 | 0.8021 | 0.8028 | 0.8035 | 0.8041 | 0.8048 | 0.8055 |
| 6.4 | 0.8062 | 0.8069 | 0.8075 | 0.8082 | 0.8089 | 0.8096 | 0.8102 | 0.8109 | 0.8116 | 0.8122 |
| 6.5 | 0.8129 | 0.8136 | 0.8142 | 0.8149 | 0.8156 | 0.8162 | 0.8169 | 0.8176 | 0.8182 | 0.8189 |
| 6.6 | 0.8195 | 0.8202 | 0.8209 | 0.8215 | 0.8222 | 0.8228 | 0.8235 | 0.8241 | 0.8248 | 0.8254 |
| 6.7 | 0.8261 | 0.8267 | 0.8274 | 0.8280 | 0.8287 | 0.8293 | 0.8299 | 0.8306 | 0.8312 | 0.8319 |
| 6.8 | 0.8325 | 0.8331 | 0.8338 | 0.8344 | 0.8351 | 0.8357 | 0.8363 | 0.8370 | 0.8376 | 0.8382 |
| 6.9 | 0.8388 | 0.8395 | 0.8401 | 0.8407 | 0.8414 | 0.8420 | 0.8426 | 0.8432 | 0.8439 | 0.8445 |
| 7.0 | 0.8451 | 0.8457 | 0.8463 | 0.8470 | 0.8476 | 0.8482 | 0.8488 | 0.8494 | 0.8500 | 0.8506 |
| 7.1 | 0.8513 | 0.8519 | 0.8525 | 0.8531 | 0.8537 | 0.8543 | 0.8549 | 0.8555 | 0.8561 | 0.8567 |
| 7.2 | 0.8573 | 0.8579 | 0.8585 | 0.8591 | 0.8597 | 0.8603 | 0.8609 | 0.8615 | 0.8621 | 0.8627 |
| 7.3 | 0.8633 | 0.8639 | 0.8645 | 0.8651 | 0.8657 | 0.8663 | 0.8669 | 0.8675 | 0.8681 | 0.8686 |
| 7.4 | 0.8692 | 0.8698 | 0.8704 | 0.8710 | 0.8716 | 0.8722 | 0.8727 | 0.8733 | 0.8739 | 0.8745 |
| 7.5 | 0.8751 | 0.8756 | 0.8762 | 0.8768 | 0.8774 | 0.8779 | 0.8785 | 0.8791 | 0.8797 | 0.8802 |
| 7.6 | 0.8808 | 0.8814 | 0.8820 | 0.8825 | 0.8831 | 0.8837 | 0.8842 | 0.8848 | 0.8854 | 0.8859 |
| 7.7 | 0.8865 | 0.8871 | 0.8876 | 0.8882 | 0.8887 | 0.8893 | 0.8899 | 0.8904 | 0.8910 | 0.8915 |
| 7.8 | 0.8921 | 0.8927 | 0.8932 | 0.8938 | 0.8943 | 0.8949 | 0.8954 | 0.8960 | 0.8965 | 0.8971 |
| 7.9 | 0.8976 | 0.8982 | 0.8987 | 0.8993 | 0.8998 | 0.9004 | 0.9009 | 0.9015 | 0.9020 | 0.9025 |
| 8.0 | 0.9031 | 0.9036 | 0.9042 | 0.9047 | 0.9053 | 0.9058 | 0.9063 | 0.9069 | 0.9074 | 0.9079 |
| 8.1 | 0.9085 | 0.9090 | 0.9096 | 0.9101 | 0.9106 | 0.9112 | 0.9117 | 0.9122 | 0.9128 | 0.9133 |
| 8.2 | 0.9138 | 0.9143 | 0.9149 | 0.9154 | 0.9159 | 0.9165 | 0.9170 | 0.9175 | 0.9180 | 0.9186 |
| 8.3 | 0.9191 | 0.9196 | 0.9201 | 0.9206 | 0.9212 | 0.9217 | 0.9222 | 0.9227 | 0.9232 | 0.9238 |
| 8.4 | 0.9243 | 0.9248 | 0.9253 | 0.9258 | 0.9263 | 0.9269 | 0.9274 | 0.9279 | 0.9284 | 0.9289 |
| 8.5 | 0.9294 | 0.9299 | 0.9304 | 0.9309 | 0.9315 | 0.9320 | 0.9325 | 0.9330 | 0.9335 | 0.9340 |
| 8.6 | 0.9345 | 0.9350 | 0.9355 | 0.9360 | 0.9365 | 0.9370 | 0.9375 | 0.9380 | 0.9385 | 0.9390 |
| 8.7 | 0.9395 | 0.9400 | 0.9405 | 0.9410 | 0.9415 | 0.9420 | 0.9425 | 0.9430 | 0.9435 | 0.9440 |
| 8.8 | 0.9445 | 0.9450 | 0.9455 | 0.9460 | 0.9465 | 0.9469 | 0.9474 | 0.9479 | 0.9484 | 0.9489 |
| 8.9 | 0.9494 | 0.9499 | 0.9504 | 0.9509 | 0.9513 | 0.9518 | 0.9523 | 0.9528 | 0.9533 | 0.9538 |
| 9.0 | 0.9542 | 0.9547 | 0.9552 | 0.9557 | 0.9562 | 0.9566 | 0.9571 | 0.9576 | 0.9581 | 0.9586 |
| 9.1 | 0.9590 | 0.9595 | 0.9600 | 0.9605 | 0.9609 | 0.9614 | 0.9619 | 0.9624 | 0.9628 | 0.9633 |
| 9.2 | 0.9638 | 0.9643 | 0.9647 | 0.9652 | 0.9657 | 0.9661 | 0.9666 | 0.9671 | 0.9675 | 0.9680 |
| 9.3 | 0.9685 | 0.9689 | 0.9694 | 0.9699 | 0.9703 | 0.9708 | 0.9713 | 0.9717 | 0.9722 | 0.9727 |
| 9.4 | 0.9731 | 0.9736 | 0.9741 | 0.9745 | 0.9750 | 0.9754 | 0.9759 | 0.9763 | 0.9768 | 0.9773 |
| 9.5 | 0.9777 | 0.9782 | 0.9786 | 0.9791 | 0.9795 | 0.9800 | 0.9805 | 0.9809 | 0.9814 | 0.9818 |
| 9.6 | 0.9823 | 0.9827 | 0.9832 | 0.9836 | 0.9841 | 0.9845 | 0.9850 | 0.9854 | 0.9859 | 0.9863 |
| 9.7 | 0.9868 | 0.9872 | 0.9877 | 0.9881 | 0.9886 | 0.9890 | 0.9894 | 0.9899 | 0.9903 | 0.9908 |
| 9.8 | 0.9912 | 0.9917 | 0.9921 | 0.9926 | 0.9930 | 0.9934 | 0.9939 | 0.9943 | 0.9948 | 0.9952 |
| 9.9 | 0.9956 | 0.9961 | 0.9965 | 0.9969 | 0.9974 | 0.9978 | 0.9983 | 0.9987 | 0.9991 | 0.9996 |
[解答へ]
[3] kを0でない実数とし、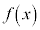 を2次関数とする。
を2次関数とする。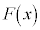 と
と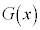 はどちらも導関数が
はどちらも導関数が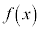 であるような関数で、
であるような関数で、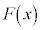 は
は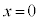 で極小値0をとり、
で極小値0をとり、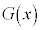 は
は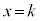 で極大値0をとるとする。
で極大値0をとるとする。
(1) まず、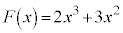 の場合を考える。
の場合を考える。 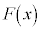 の導関数が
の導関数が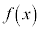 であることから
であることからであり、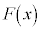 は
は で極大値をとる。また、
で極大値をとる。また、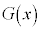 の導関数が
の導関数が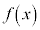 であることから
であることから 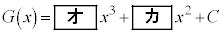 (Cは積分定数)
(Cは積分定数)と表され、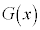 は
は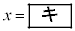 で極小値をとる。さらに
で極小値をとる。さらに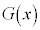 に関する条件から
に関する条件から である。
である。
(2) 次に、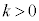 の場合を考える。
の場合を考える。 このとき、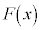 と
と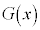 に関する条件から、
に関する条件から、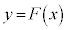 のグラフと
のグラフと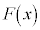 ,
,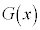 の極値について調べよう。
の極値について調べよう。
(i) 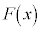 が
が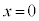 で極値をとることから、
で極値をとることから、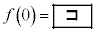 であり、
であり、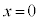 の前後で
の前後で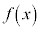 の符号は
の符号は 。さらに、
。さらに、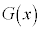 が
が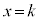 で極大値をとることから、
で極大値をとることから、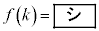 であり、
であり、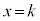 の前後で
の前後で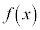 の符号は
の符号は 。したがって、
。したがって、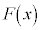 の導関数は
の導関数は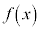 であることに注意すると、座標平面において
であることに注意すると、座標平面において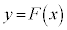 のグラフの概形は
のグラフの概形は であることがわかる。
であることがわかる。  ,
, の解答群(同じものを繰り返し選んでもよい)
の解答群(同じものを繰り返し選んでもよい) 負から正に変わる
負から正に変わる  正から負に変わる
正から負に変わる  変わらない
変わらない
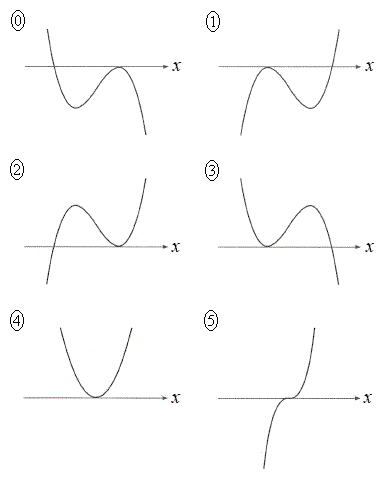
 については、最も適当なものを、右の
については、最も適当なものを、右の ~
~ のうちから一つ選べ。なお、y軸は省略しているが、上方向が正の方向であり、x軸は直線
のうちから一つ選べ。なお、y軸は省略しているが、上方向が正の方向であり、x軸は直線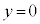 を表している。
を表している。(ii) 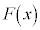 に関する条件から、すべての実数xに対して
に関する条件から、すべての実数xに対して
が成り立つ。このことと(i)の考察により、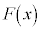 の極大値は
の極大値は と表され、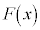 の極大値は、関数
の極大値は、関数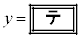 のグラフとx軸で囲まれた図形の
のグラフとx軸で囲まれた図形の と等しいことがわかる。
と等しいことがわかる。
さらに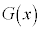 に関する条件から、
に関する条件から、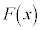 の極大値は、
の極大値は、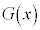 の
の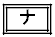 と等しいことがわかる。
と等しいことがわかる。
 ~
~ の解答群(同じものを繰り返し選んでもよい。)
の解答群(同じものを繰り返し選んでもよい。) 0
0  1
1  k
k  x
x の解答群
の解答群

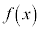

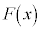

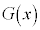
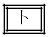 の解答群
の解答群
 面積
面積  面積の-1倍
面積の-1倍
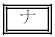 の解答群
の解答群
 極小値
極小値  極大値
極大値
 極小値の-1倍
極小値の-1倍  極大値の-1倍
極大値の-1倍
[解答へ]
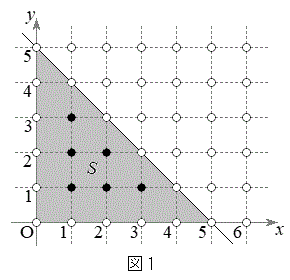
[4] 座標平面上で、x座標とy座標がともに整数である点を格子点という。いくつかの直線や曲線で囲まれた図形の内部にある格子点の個数を考えよう。ただし、図形の内部は、境界(境界線)を含まないものとする。
 例えば、直線
例えば、直線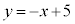 とx軸,y軸で囲まれた図形をSとする。Sは図1の灰色部分であり、Sの内部にある格子点を黒丸、内部にない格子点を白丸で表している。したがって、Sの内部にある格子点の個数は6である。
とx軸,y軸で囲まれた図形をSとする。Sは図1の灰色部分であり、Sの内部にある格子点を黒丸、内部にない格子点を白丸で表している。したがって、Sの内部にある格子点の個数は6である。
(1) 直線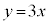 とx軸、直線
とx軸、直線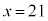 で囲まれた図形をTとする。Tの内部にある格子点の個数を考える。
で囲まれた図形をTとする。Tの内部にある格子点の個数を考える。 直線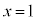 上の格子点でTの内部にあるものは、点
上の格子点でTの内部にあるものは、点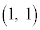 と点
と点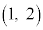 の2個である。点
の2個である。点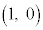 と点
と点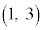 はTの境界にあるため、内部にはない。nを整数とする。直線
はTの境界にあるため、内部にはない。nを整数とする。直線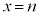 がTの内部にある格子点を通るのは、
がTの内部にある格子点を通るのは、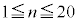 のときである。
のときである。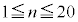 のとき、直線
のとき、直線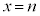 上の格子点でTの内部にあるものの個数を
上の格子点でTの内部にあるものの個数を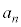 とおく。
とおく。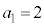 であり、
であり、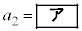 ,
,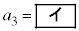 である。数列
である。数列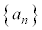 は
は が
が の
の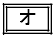 数列である。
数列である。
したがって、Tの内部にある格子点の個数は である。
である。
 の解答群
の解答群
 公差
公差  公比
公比
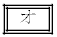 の解答群
の解答群
 等差
等差  等比
等比
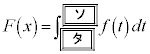
(2) nを自然数とする。関数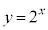 のグラフとx軸,y軸および直線
のグラフとx軸,y軸および直線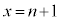 で囲まれた図形をUとする。
で囲まれた図形をUとする。 kを整数とする。直線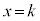 がUの内部にある格子点を通るとき、直線
がUの内部にある格子点を通るとき、直線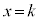 上の格子点でUの内部にあるものの個数は
上の格子点でUの内部にあるものの個数は である。
である。
したがって、Uの内部にある格子点の個数は
(3) a,b,cは整数で、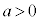 ,
,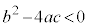 を満たすとする。放物線
を満たすとする。放物線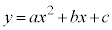 とx軸、y軸および直線
とx軸、y軸および直線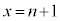 で囲まれた図形をVとする。すべての自然数nに対して、Vの内部にある格子点の個数が
で囲まれた図形をVとする。すべての自然数nに対して、Vの内部にある格子点の個数が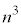 となるのは、
となるのは、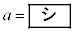 ,
, ,
,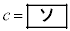 のときである。
のときである。
[解答へ]
[5] 以下の問題を解答するにあたっては、必要に応じて問題末の正規分布表を用いてもよい。
Q地域ではレモンを栽培しており、収穫されるレモンを重さによってサイズごとに分類している(表1)。過去に収穫されたレモンは、平均が110g,標準偏差が20gの正規分布に従うとする。
表1 レモンのサイズと重さの対応関係
| サイズ | レモン1個の重さ |
| S | 80g以上90g未満 |
| M | 90g以上110g未満 |
| L | 110g以上140g未満 |
| 2L | 140g以上170g未満 |
| その他 | 80g未満または170g以上 |
(1) Q地域で今年収穫されるレモンの重さ(単位はg)は、過去に収穫されたレモンの重さと同じ分布に従うものとする。すなわち、今年収穫される1個のレモンの重さを確率変数Xで表すと、Xは正規分布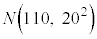 に従うとする。よって、今年収穫されるレモンから無作為にレモンを1個抽出するとき、そのレモンがLサイズである確率は、
に従うとする。よって、今年収穫されるレモンから無作為にレモンを1個抽出するとき、そのレモンがLサイズである確率は、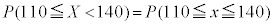 であることに注意すると、
であることに注意すると、 である。
である。 いま、Q地域で今年収穫されるレモンが20万個であるとし、その中のLサイズのレモンの個数を確率変数Yで表すと、Yは二項分布に従い、Yの平均(期待値)は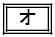 となる。
となる。
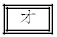 については、最も適当なものを、次の
については、最も適当なものを、次の ~
~ のうちから一つ選べ。
のうちから一つ選べ。
 13100
13100  13360
13360  31740
31740  68260
68260  86640
86640  10000
10000  168260
168260  16640
16640
(2) 太郎さんと花子さんは、Q地域で今年収穫されるレモンから何個かを抽出して、今年収穫されるレモンの重さの平均(母平均)を推定する方法について話している。
太郎:母平均に対する信頼度95%の信頼区間の幅を4g以下にして推定したいね。
花子:母標準偏差を過去と同じ20gとすると、何個のレモンの重さを量ればいいかな。
太郎:信頼区間の式から、必要な標本の大きさを求めてみようよ。
母平均に対する信頼度95%の信頼区間の幅を4g以下にするために必要な標本の大きさを求める。いま、Q地域で今年収穫されるレモン全体を母集団とし、その重さの母平均をmg,母標準偏差をσgとする。この母集団から無作為に抽出したn個のレモンの重さを確率変数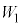 ,
,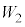 ,・・・,
,・・・,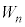 で表すと、標本の大きさnが十分に大きいとき、標本平均
で表すと、標本の大きさnが十分に大きいとき、標本平均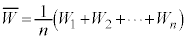 は近似的に正規分布
は近似的に正規分布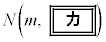 に従う。また、mに対する信頼度95%の信頼区間
に従う。また、mに対する信頼度95%の信頼区間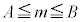 と表すと、信頼区間の幅は
と表すと、信頼区間の幅は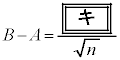 となる。
となる。
したがって、母標準偏差を過去と同じ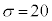 として、nに関する不等式
として、nに関する不等式 を満たす自然数nを求めればよい。①の両辺は正であるから、両辺を2乗して整理すると、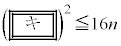 となる。この不等式を満たす最小の自然数nを
となる。この不等式を満たす最小の自然数nを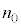 とすると、
とすると、 である。ゆえに、mに対する信頼度95%の信頼区間の幅を4g以下にするために必要な標本の大きさnのうち、最小のものは
である。ゆえに、mに対する信頼度95%の信頼区間の幅を4g以下にするために必要な標本の大きさnのうち、最小のものは であることがわかる。
であることがわかる。
 の解答群
の解答群
 σ
σ 
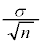

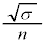

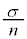

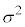

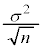

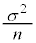

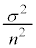
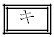 については、最も適当なものを、次の
については、最も適当なものを、次の ~
~ のうちから一つ選べ。
のうちから一つ選べ。
 σ
σ 
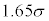

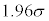

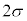

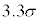

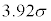
(3) 太郎さんと花子さんは、Q地域で今年収穫されるレモンの重さについて話している。
太郎:今年のレモンの重さは、他の地域では例年よりも軽そうだと聞いたよ。
花子:Q地域でも、過去の平均110gと比べて軽いのかな。
太郎:標本の大きさを400,母標準偏差を過去と同じ20gとして、仮説検定をしてみようよ。
(2)のmを用いて、Q地域で今年収穫されるレモンの重さの母平均mgが過去の平均110gより軽いといえるかを、有意水準5%(0.05)で仮説検定を行い検証したい。ただし、標本の大きさは400,母標準偏差は過去と同じ20gとする。
ここで、統計的に検証したい仮説を「対立仮説」、対立仮説に反する過程として設けた仮説を「帰無仮説」とする。このとき、帰無仮説は「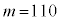 」、対立仮説は「
」、対立仮説は「 」である。これらの仮説に対して、有意水準5%で帰無仮説が棄却(否定)されるかどうかを判断する。
」である。これらの仮説に対して、有意水準5%で帰無仮説が棄却(否定)されるかどうかを判断する。
いま、帰無仮説が正しいと仮定する。標本の大きさ400は十分に大きいので、(2)の標本平均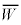 は近似的に正規分布
は近似的に正規分布 に従う。無作為抽出した400個のレモンの重さの平均が108.2gとなった。このとき、確率
に従う。無作為抽出した400個のレモンの重さの平均が108.2gとなった。このとき、確率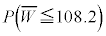 は
は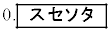 となる。この値をパーセント表示した値は有意水準5%より
となる。この値をパーセント表示した値は有意水準5%より 。したがって、有意水準5%で今年収穫されるレモンの重さの母平均は110gより軽いと
。したがって、有意水準5%で今年収穫されるレモンの重さの母平均は110gより軽いと 。
。
 の解答群
の解答群

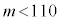

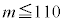

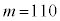

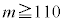

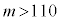
 の解答群
の解答群

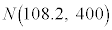

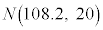

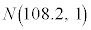

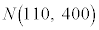

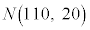

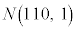
 の解答群
の解答群
 小さいから、帰無仮説は棄却されない
小さいから、帰無仮説は棄却されない
 小さいから、帰無仮説は棄却される
小さいから、帰無仮説は棄却される
 大きいから、帰無仮説は棄却されない
大きいから、帰無仮説は棄却されない
 大きいから、帰無仮説は棄却される
大きいから、帰無仮説は棄却される
 の解答群
の解答群
 判断できる
判断できる  判断できない
判断できない
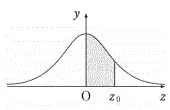
正規分布表
次の表は、標準正規分布の分布曲線における右図灰色
部分の面積をまとめたものである。
 | 0.00 | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 |
| 0.0 | 0.0000 | 0.0040 | 0.0080 | 0.0120 | 0.0160 | 0.0199 | 0.0239 | 0.0279 | 0.0319 | 0.0359 |
| 0.1 | 0.0398 | 0.0438 | 0.0478 | 0.0517 | 0.0557 | 0.0596 | 0.0636 | 0.0675 | 0.0714 | 0.0753 |
| 0.2 | 0.0793 | 0.0832 | 0.0871 | 0.0910 | 0.0948 | 0.0987 | 0.1026 | 0.1064 | 0.1103 | 0.1141 |
| 0.3 | 0.1179 | 0.1217 | 0.1255 | 0.1293 | 0.1331 | 0.1368 | 0.1406 | 0.1443 | 0.1480 | 0.1517 |
| 0.4 | 0.1554 | 0.1591 | 0.1628 | 0.1664 | 0.1700 | 0.1736 | 0.1772 | 0.1808 | 0.1844 | 0.1879 |
| 0.5 | 0.1915 | 0.1950 | 0.1985 | 0.2019 | 0.2054 | 0.2088 | 0.2123 | 0.2157 | 0.2190 | 0.2224 |
| 0.6 | 0.2257 | 0.2291 | 0.2324 | 0.2357 | 0.2389 | 0.2422 | 0.2454 | 0.2486 | 0.2517 | 0.2549 |
| 0.7 | 0.2580 | 0.2611 | 0.2642 | 0.2673 | 0.2704 | 0.2734 | 0.2764 | 0.2794 | 0.2823 | 0.2852 |
| 0.8 | 0.2881 | 0.2910 | 0.2939 | 0.2967 | 0.2995 | 0.3023 | 0.3051 | 0.3078 | 0.3106 | 0.3133 |
| 0.9 | 0.3159 | 0.3186 | 0.3212 | 0.3238 | 0.3264 | 0.3289 | 0.3315 | 0.3340 | 0.3365 | 0.3389 |
| 1.0 | 0.3413 | 0.3438 | 0.3461 | 0.3485 | 0.3508 | 0.3531 | 0.3554 | 0.3577 | 0.3599 | 0.3621 |
| 1.1 | 0.3643 | 0.3665 | 0.3686 | 0.3708 | 0.3729 | 0.3749 | 0.3770 | 0.3790 | 0.3810 | 0.3830 |
| 1.2 | 0.3849 | 0.3869 | 0.3888 | 0.3907 | 0.3925 | 0.3944 | 0.3962 | 0.3980 | 0.3997 | 0.4015 |
| 1.3 | 0.4032 | 0.4049 | 0.4066 | 0.4082 | 0.4099 | 0.4115 | 0.4131 | 0.4147 | 0.4162 | 0.4177 |
| 1.4 | 0.4192 | 0.4207 | 0.4222 | 0.4236 | 0.4251 | 0.4265 | 0.4279 | 0.4292 | 0.4306 | 0.4319 |
| 1.5 | 0.4332 | 0.4345 | 0.4357 | 0.4370 | 0.4382 | 0.4394 | 0.4406 | 0.4418 | 0.4429 | 0.4441 |
| 1.6 | 0.4452 | 0.4463 | 0.4474 | 0.4484 | 0.4495 | 0.4505 | 0.4515 | 0.4525 | 0.4535 | 0.4545 |
| 1.7 | 0.4554 | 0.4564 | 0.4573 | 0.4582 | 0.4591 | 0.4599 | 0.4608 | 0.4616 | 0.4625 | 0.4633 |
| 1.8 | 0.4641 | 0.4649 | 0.4656 | 0.4664 | 0.4671 | 0.4678 | 0.4686 | 0.4693 | 0.4699 | 0.4706 |
| 1.9 | 0.4713 | 0.4719 | 0.4726 | 0.4732 | 0.4738 | 0.4744 | 0.4750 | 0.4756 | 0.4761 | 0.4767 |
| 2.0 | 0.4772 | 0.4778 | 0.4783 | 0.4788 | 0.4793 | 0.4798 | 0.4803 | 0.4808 | 0.4812 | 0.4817 |
| 2.1 | 0.4821 | 0.4826 | 0.4830 | 0.4834 | 0.4838 | 0.4842 | 0.4846 | 0.4850 | 0.4854 | 0.4857 |
| 2.2 | 0.4861 | 0.4864 | 0.4868 | 0.4871 | 0.4875 | 0.4878 | 0.4881 | 0.4884 | 0.4887 | 0.4890 |
| 2.3 | 0.4893 | 0.4896 | 0.4898 | 0.4901 | 0.4904 | 0.4906 | 0.4909 | 0.4911 | 0.4913 | 0.4916 |
| 2.4 | 0.4918 | 0.4920 | 0.4922 | 0.4925 | 0.4927 | 0.4929 | 0.4931 | 0.4932 | 0.4934 | 0.4936 |
| 2.5 | 0.4938 | 0.4940 | 0.4941 | 0.4943 | 0.4945 | 0.4946 | 0.4948 | 0.4949 | 0.4951 | 0.4952 |
| 2.6 | 0.4953 | 0.4955 | 0.4956 | 0.4957 | 0.4959 | 0.4960 | 0.4961 | 0.4962 | 0.4963 | 0.4964 |
| 2.7 | 0.4965 | 0.4966 | 0.4967 | 0.4968 | 0.4969 | 0.4970 | 0.4971 | 0.4972 | 0.4973 | 0.4974 |
| 2.8 | 0.4974 | 0.4975 | 0.4976 | 0.4977 | 0.4977 | 0.4978 | 0.4979 | 0.4979 | 0.4980 | 0.4981 |
| 2.9 | 0.4981 | 0.4982 | 0.4982 | 0.4983 | 0.4984 | 0.4984 | 0.4985 | 0.4985 | 0.4986 | 0.4986 |
| 3.0 | 0.4987 | 0.4987 | 0.4987 | 0.4988 | 0.4988 | 0.4989 | 0.4989 | 0.4989 | 0.4990 | 0.4990 |
| 3.1 | 0.4990 | 0.4991 | 0.4991 | 0.4991 | 0.4992 | 0.4992 | 0.4992 | 0.4992 | 0.4993 | 0.4993 |
| 3.2 | 0.4993 | 0.4993 | 0.4994 | 0.4994 | 0.4994 | 0.4994 | 0.4994 | 0.4995 | 0.4995 | 0.4995 |
| 3.3 | 0.4995 | 0.4995 | 0.4995 | 0.4996 | 0.4996 | 0.4996 | 0.4996 | 0.4996 | 0.4996 | 0.4997 |
| 3.4 | 0.4997 | 0.4997 | 0.4997 | 0.4997 | 0.4997 | 0.4997 | 0.4997 | 0.4997 | 0.4997 | 0.4998 |
| 3.5 | 0.4998 | 0.4998 | 0.4998 | 0.4998 | 0.4998 | 0.4998 | 0.4998 | 0.4998 | 0.4998 | 0.4998 |
[解答へ]
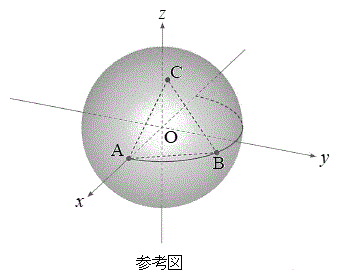 [6] Oを原点とする座標空間において、Oを中心とする半径1の球面をSとする。S上に二つの点
[6] Oを原点とする座標空間において、Oを中心とする半径1の球面をSとする。S上に二つの点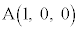 ,
,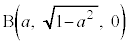 をとる。ただし、aは
をとる。ただし、aは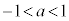 を満たす実数とする。S上の点Cを、△ABCが正三角形となるようにとれるかどうかを考えてみよう。
を満たす実数とする。S上の点Cを、△ABCが正三角形となるようにとれるかどうかを考えてみよう。
(1) 点Cの座標を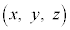 とする。CがS上にあるとき
とする。CがS上にあるとき である。これをベクトル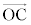 の成分を用いて表すと
の成分を用いて表すと 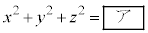 ・・・①
・・・①となる。
さらに、△ABCが正三角形であるとする。△OACと△OABは、対応する三組の辺の長さがそれぞれ等しいから合同である。したがって、対応する角の大きさも等しいから
が成り立つ。これをベクトルの成分を用いて表すと
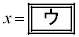 ・・・②
・・・②となる。同様に△OBCと△OABも合同であるから
が成り立ち、これをベクトルの成分を用いて表すと
 ・・・③
・・・③となる。
逆に、実数x,y,zが①,②,③を満たすとき、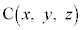 はS上の点であり、△ABCは正三角形になっていることがわかる。
はS上の点であり、△ABCは正三角形になっていることがわかる。
 の解答群
の解答群 > 0
> 0  1
1 
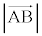

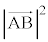

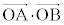

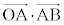
 ~
~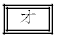 の解答群(同じものを繰り返し選んでもよい)
の解答群(同じものを繰り返し選んでもよい) a
a 
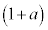

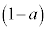

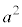

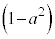

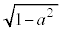
(2) aに具体的な値を代入して、△ABCが正三角形となるS上の点Cがあるかどうかを調べよう。
(i) 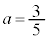 のとき、②と③を満たす実数x,yは
のとき、②と③を満たす実数x,yは 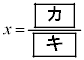 ,
,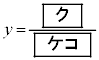
である。このx,yに対して、①を満たす実数zは 。したがって、△ABCが正三角形となるS上の点Cは
。したがって、△ABCが正三角形となるS上の点Cは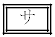 。
。 (ii) 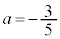 のときも調べよう。(i)と同様に考えると、△ABCが正三角形となるS上の点Cは
のときも調べよう。(i)と同様に考えると、△ABCが正三角形となるS上の点Cは ことがわかる。
ことがわかる。 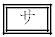 ,
, の解答群(同じものを繰り返し選んでもよい)
の解答群(同じものを繰り返し選んでもよい) ない
ない  ちょうど一つある
ちょうど一つある  ちょうど二つある
ちょうど二つある  ちょうど三つある
ちょうど三つある  ちょうど四つある
ちょうど四つある  無限に多くある
無限に多くある
(3) △ABCが正三角形となるS上の点Cがあるための、aに関する条件を見つけよう。
実数x,y,zは、①,②,③を満たすとする。②と③から
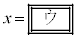 ,
,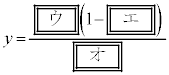
である。このとき、①から
となる。さらに、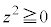 ,
,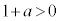 であるから
であるから である。
である。
逆に のとき、①,②,③を満たす実数x,y,zがあることがわかる。
のとき、①,②,③を満たす実数x,y,zがあることがわかる。
以上のことから、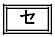 は、△ABCが正三角形となるS上の点Cがあるための必要十分条件である。
は、△ABCが正三角形となるS上の点Cがあるための必要十分条件である。
 の解答群
の解答群

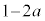

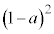

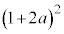

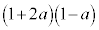

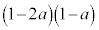

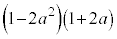

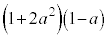

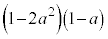
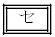 の解答群
の解答群

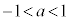

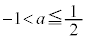

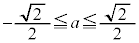

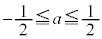

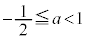

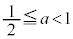

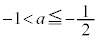 または
または 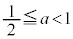

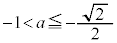 または
または 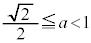
[解答へ]
[7] α,β,γを異なる複素数とし、複素数平面上に3点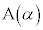 ,
,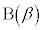 ,
,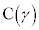 をとる。直線ABと直線ACの関係について考えよう。
をとる。直線ABと直線ACの関係について考えよう。
以下、複素数の偏角は0以上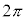 未満とする。
未満とする。
であるから
であり、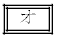 の偏角は
の偏角は である。
である。
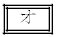 の解答群
の解答群
 i
i 
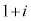
 2
2 
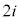

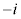

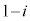

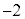


 の解答群
の解答群
 0
0 
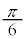

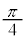

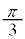

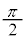

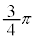
 π
π 
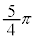
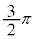
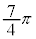
(2) 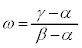 とおく。直線ABと直線ACが垂直に交わるのは、ωの偏角が
とおく。直線ABと直線ACが垂直に交わるのは、ωの偏角が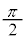 または
または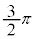 のときである。このとき、ωは
のときである。このとき、ωは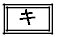 であるから
であるから である。逆に、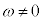 に注意すると、
に注意すると、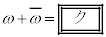 のとき、ωは
のとき、ωは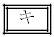 であるので、直線ABと直線ACが垂直に交わる。
であるので、直線ABと直線ACが垂直に交わる。
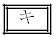 の解答群
の解答群
 0でない実数
0でない実数 
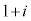 または
または 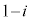
 純虚数(実部が0である虚数)
純虚数(実部が0である虚数) 
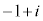 または
または 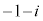
 の解答群
の解答群
 0
0  1
1  2
2  i
i 
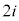

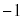

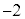

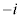
(3) zは0,2,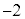 でない複素数とする。
でない複素数とする。
(i) 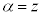 ,
,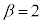 ,
,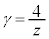 とする。直線ABと直線ACが垂直に交わるための条件について考えよう。
とする。直線ABと直線ACが垂直に交わるための条件について考えよう。 が成り立つので、直線ABと直線ACが垂直に交わるための必要十分条件は
である。これは、
(ii) (i)のα,β,γをそれぞれ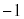 倍した複素数
倍した複素数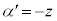 ,
,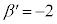 ,
,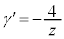 について考える。複素数平面上の異なる3点
について考える。複素数平面上の異なる3点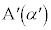 ,
,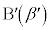 ,
,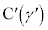 について、直線
について、直線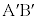 と直線
と直線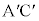 が垂直になるような点z全体を複素数平面上に図示すると
が垂直になるような点z全体を複素数平面上に図示すると である。
である。
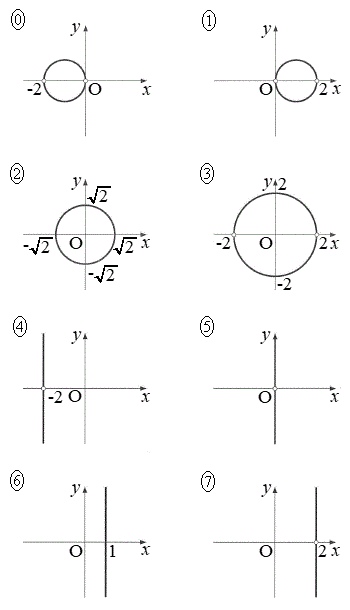 (iii) (i)のα,β,γにおけるzを
(iii) (i)のα,β,γにおけるzを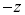 に置き換え、
に置き換え、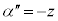 ,
,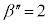 ,
,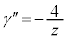 について考える。複素数平面上の異なる3点
について考える。複素数平面上の異なる3点 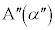 ,
,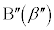 ,
,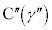 について、直線
について、直線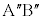 と直線
と直線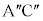 が垂直になるような点z全体を複素数平面上に図示すると
が垂直になるような点z全体を複素数平面上に図示すると である。
である。 ,
, については、最も適当なものを、右の
については、最も適当なものを、右の ~
~ のうちから一つ選べ。ただし、同じものを繰り返し選んでもよい。
のうちから一つ選べ。ただし、同じものを繰り返し選んでもよい。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2025(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 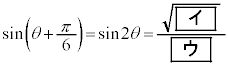


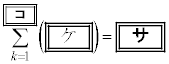
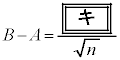 となる。
となる。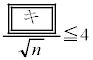
 ,
,