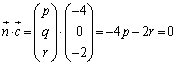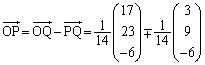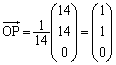�d�ʑ吔�w'08�N�O��[4]
xyz���W��ԓ��ɂ����āA�_P�𒆐S�Ƃ����a��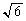 �̋���S���l����B���镽��α�Ƌ���S��������Ăł���~D���3�_A
�̋���S���l����B���镽��α�Ƌ���S��������Ăł���~D���3�_A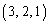 �CB
�CB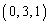 �CC
�CC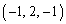 ������B�ȉ��̖₢�ɓ�����B�������A
������B�ȉ��̖₢�ɓ�����B�������A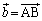 �C
�C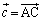 �Ƃ���B
�Ƃ���B
(1) ����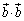 �C
�C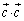 �����
�����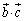 �̒l�����߂�B
�̒l�����߂�B (2) �~D�̒��S��Q�Ƃ���B�_Q�͕���α��ɂ���̂ŁA�x�N�g��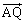 �͂������s�Ct��p����
�͂������s�Ct��p���� �ƕ\�����B����AB�CAC�̒��_�����ꂼ��M�CN�Ƃ���Ƃ��A�x�N�g��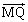 �C
�C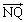 ��s�Ct�C
��s�Ct�C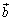 �C
�C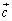 ��p���ĕ\���B
��p���ĕ\���B (3) s�Ct�̒l�����߂�B
(4) �~D�̔��ar�ƒ��SQ�̍��W�����߂�B
(5) ����α�Ɛ����ȃx�N�g��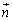 �𐬕��ŕ\���B
�𐬕��ŕ\���B (6) ����S�̒��SP�̍��W�����߂�B�������A�_P��z���W�͕��łȂ��Ƃ���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�����v�Z�ɂ���āA�������݂����_�̈ʒu�����߂Ă����A�P�Ȃ��ԃx�N�g���̌v�Z���ł����A�K�x�ɕ��G�ŁA�Z���^�[�������K�p�Ƃ��Ă��傤�Ǘǂ��Ǝv���܂��B��ԃx�N�g�������Ƃ���l�́A�����������ɂ���������g��ł����Ă��������B
(2)�ɂ��ẮA�x�N�g����1���Ɨ����Q�Ƃ��Ă��������B
(1) 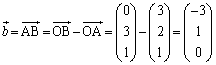
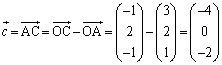
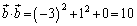 ......[��]
......[��]
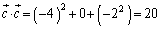 ......[��]
......[��]
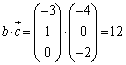 ......[��]
......[��]
(2) 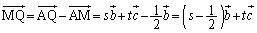 ......[��]
......[��] 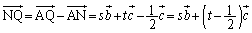 ......[��]
......[��]
(3) 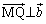 ���A
���A �� 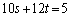 �@����@
�@����@
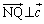 ���A
���A �� 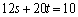 �@����A
�@����A
�A�~5�|�@�~6���A �� 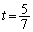 �@ ......[��]�@�ɑ�����āA
�@ ......[��]�@�ɑ�����āA �� 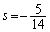 �@ ......[��]
�@ ......[��]
(4) 
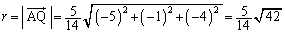 ......[��]
......[��]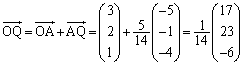
Q�̍��W�́A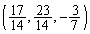 ......[��]
......[��]
(5) ����α�Ɛ����ȃx�N�g���́A����α��̃x�N�g��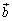 �C
�C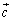 �Ƃ������ł��B
�Ƃ������ł��B �Ƃ����ƁA �C
�C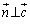 ���A
���A 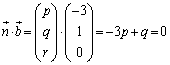 �C
�C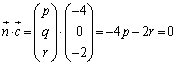
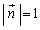 ���A
���A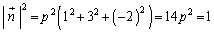
�� 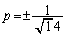 ��
�� 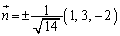 ......[��]
......[��]
(6) 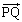 �ƕ���α�͐����Ȃ̂ŁA
�ƕ���α�͐����Ȃ̂ŁA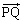 //
// 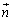 �ł��B
�ł��B �܂��A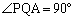 �Ȃ̂ŎO�����̒藝���A
�Ȃ̂ŎO�����̒藝���A �� 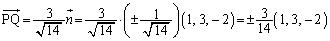
�_P��z���W�͕��ł͂Ȃ��̂ŁA�}�́A�}�C�i�X�̕����̂��āA
����āAP�̍��W�́A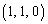 ......[��]
......[��]
�NjL�D(5)�ŁA2�̃x�N�g���ɐ����ȃx�N�g�������߂Ă��܂��B�{��̂悤�Ș_�q���ł͎g���܂��A��[���ł͗L���ȋZ�I���m���Ă��܂��B
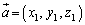 �C
�C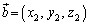 �ł���Ƃ��A
�ł���Ƃ��A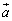 ��
��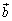 ���O���F
���O���F
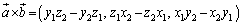 �@
�@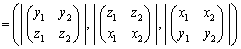
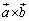 �́A
�́A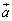 �C
�C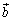 �̑o���Ɛ����ł��邱�Ƃ��m���߂邱�Ƃ��ł��܂�(�O�����Q��)�B������ŏؖ����Ă��Ă͉����ɂȂ�̂ŁA��[���̂Ƃ��ɁA�u2�̃x�N�g����y�Cz�����ō�����s����x�����Cz�Cx�����ō�����s��y�����Ax�Cy�����ō�����s��z�����Ƃ���x�N�g���́A���Ƃ�2�̃x�N�g���ɐ����Ȃ�v���Ƃ��L�����Ă����Ďg���Ƃ悢�Ǝv���܂��B
�̑o���Ɛ����ł��邱�Ƃ��m���߂邱�Ƃ��ł��܂�(�O�����Q��)�B������ŏؖ����Ă��Ă͉����ɂȂ�̂ŁA��[���̂Ƃ��ɁA�u2�̃x�N�g����y�Cz�����ō�����s����x�����Cz�Cx�����ō�����s��y�����Ax�Cy�����ō�����s��z�����Ƃ���x�N�g���́A���Ƃ�2�̃x�N�g���ɐ����Ȃ�v���Ƃ��L�����Ă����Ďg���Ƃ悢�Ǝv���܂��B
�{��ł́A
�ƂȂ�̂ŁA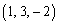 �ƕ��s�ő傫��1�̃x�N�g�������߂��
�ƕ��s�ő傫��1�̃x�N�g�������߂��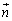 �������܂��B
�������܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 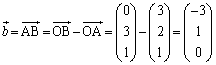
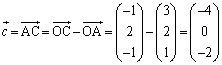
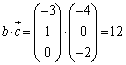 ......[��]
......[��]
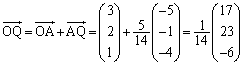
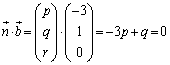 �C
�C