���É��s��㐔�w'08�N[2]
�l�ʑ�OABC�ɂ����āA �C
�C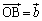 �C
�C �Ƃ���B
�Ƃ���B
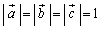 �C
�C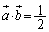 �C
�C �C
�C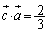 �̂Ƃ��A���̖₢�ɓ�����B
�̂Ƃ��A���̖₢�ɓ�����B
(1) ��BC��t�F �̔�ɕ�����_��Q�CAQ��s�F
�̔�ɕ�����_��Q�CAQ��s�F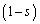 �̔�ɕ�����_��P�Ƃ���B
�̔�ɕ�����_��P�Ƃ���B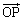 ��
��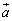 �C
�C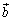 �C
�C ��s�Ct�ŕ\���B
��s�Ct�ŕ\���B (2) 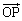 ������ABC�Ɛ����ɂȂ�Ƃ��As�Ct�̒l�����߂�B
������ABC�Ɛ����ɂȂ�Ƃ��As�Ct�̒l�����߂�B (3) �l�ʑ�OABC�̑̐ς����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�l�ʑ̂̑̐ς����߂�W���I�Ȗ��ł��B�ł����A���̖��̗U���̂܂܌v�Z����̂ł́A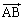 �C
�C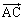 �Ƃ�������A
�Ƃ�������A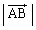 �C
�C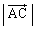 �̌v�Z������Ƃ��ɁA
�̌v�Z������Ƃ��ɁA �C
�C �Ɋւ�����ς��o�Ă��āA�W�J�����Ƃ��̍����������Ėʓ|�ł��B�����ŁA
�Ɋւ�����ς��o�Ă��āA�W�J�����Ƃ��̍����������Ėʓ|�ł��B�����ŁA
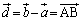 �C
�C
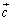 �C
�C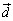 �C
�C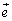 ��3�̃x�N�g���̑g�ōl���邱�Ƃɂ��܂��B
��3�̃x�N�g���̑g�ōl���邱�Ƃɂ��܂��B
�� 
�� 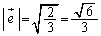
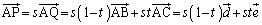
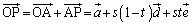 �@����@
�@����@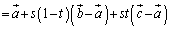
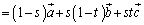 ......[��]
......[��]�@��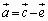 ���A
���A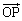 ��
��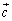 �C
�C �C
�C ���g���ĕ\���ƁA
���g���ĕ\���ƁA 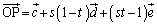 �@����A
�@����A
(2)  ������ABC�Ɛ����ɂȂ�Ƃ��A
������ABC�Ɛ����ɂȂ�Ƃ��A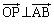 �C
�C
����āA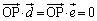 �C�A���A
�C�A���A �� 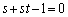 �@����C
�@����C
�C�|�B���A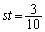
�� 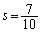 �C
�C ......[��]���̂Ƃ��A���A
......[��]���̂Ƃ��A���A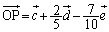
 ......[��]
......[��]
�NjL�D�ȏ�̉��A�l�ʑ�OABC�̑̐�V���A�O�p�`ABC���ʁC���_O����O�p�`ABC�ɉ��낵��������OH�Ƃ��āA
�ɂ���ċ��߂�ꍇ�ɂ́AA���n�_�Ƃ��ĎO�p�`ABC����� �C
�C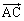 �C����сA�n�_�Ɍ������x�N�g��
�C����сA�n�_�Ɍ������x�N�g��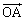 ��3�̃x�N�g������{�x�N�g���Ƃ��čl����悢�A�Ƃ������ƂɂȂ�܂��B
��3�̃x�N�g������{�x�N�g���Ƃ��čl����悢�A�Ƃ������ƂɂȂ�܂��B
�l�ʑ̂̑̐ς̖��͖{��̂悤�ɁA�e�ӂ̒����Ɗe�ӂ̃x�N�g�����m�̓��ς�^������̂ق��ɁA���_�̍��W��^����^�C�v�̖�肪����܂��B�Ⴆ�A
��㋳���'07�N[4]�F
���W��Ԃɂ����āA3�_A �CB
�CB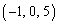 �CC
�CC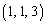 �̒�߂镽�ʂ�α�Ƃ��A���_O���畽��α�ɐ���OH�����낷�B
�̒�߂镽�ʂ�α�Ƃ��A���_O���畽��α�ɐ���OH�����낷�B (1) �O�p�`ABC�̖ʐς����߂�B
(2)  ���݂���s�Ct�����߂�B
���݂���s�Ct�����߂�B (3) �_H�̍��W�����߂�B
(4) �l�ʑ�OABC�̑̐ς����߂�B
���@�ȉ��̊e�v�Z�ɂ��ẮA��ԃx�N�g�����Q�Ƃ��Ă��������B
(1) 
�O�p�`ABC�̖ʐ�S�́A
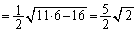 ......[��]
......[��]
(2) 

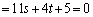 �@����@
�@����@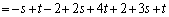
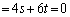 �@����A
�@����A�@�~3�|�A�~2���A
�� 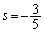 ......[��]�A���A
......[��]�A���A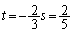 ......[��]
......[��]
(3) 
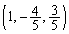 ......[��]
......[��]
(4) 
�l�ʑ�OABC�̑̐�V�́A
 ......[��]
......[��]
���́A���Z�͈̔͊O�ł����A�O���Ƃ���������g���ƁA�����ƊȒP�ɓ����邱�Ƃ��ł��܂��B
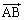 ��
��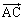 �̊O��
�̊O�� �́A
�́A
 �@(���̌v�Z�@�A�O�ς̐����ɂ��ẮA�O�����Q��)
�@(���̌v�Z�@�A�O�ς̐����ɂ��ẮA�O�����Q��)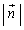 ��
��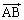 ��
��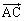 �ō�镽�s�l�ӌ`�̖ʐςɂȂ�)�A
�ō�镽�s�l�ӌ`�̖ʐςɂȂ�)�A
 ��
��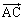 �̊O��
�̊O�� �́A�O�p�`ABC�ɐ����Ȃ̂ŁA
�́A�O�p�`ABC�ɐ����Ȃ̂ŁA
�Ƃ��āA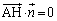 ���A
���A
�� 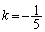 �C
�C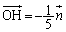
(3)��H�̍��W�́A
(4)�̎l�ʑ�OABC�̑̐�V�́A
�ƂȂ�܂��B
�Ȃ��A�l�ʑ̂̑̐����Q�Ƃ��Ă��������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B