�V���嗝�n���w'08�N[2]
A��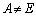 �C
�C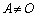 ����
����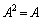 ���݂���2�������s��Ƃ���B�������A
���݂���2�������s��Ƃ���B�������A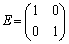 �C
�C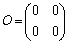 �ł���B���̂Ƃ��A���̖₢�ɓ�����B
�ł���B���̂Ƃ��A���̖₢�ɓ�����B
(1) ����t�ɑ��āA��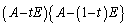 �����
�����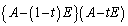 �����߂�B
�����߂�B (2) �s��A�����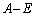 �͂Ƃ��ɋt�s��������Ȃ����Ƃ������B
�͂Ƃ��ɋt�s��������Ȃ����Ƃ������B (3) 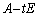 ���t�s��������߂�t�ɑ���K�v�\�����������߂�B�܂��At�����̕K�v�\���������݂����Ƃ��A�t�s��
���t�s��������߂�t�ɑ���K�v�\�����������߂�B�܂��At�����̕K�v�\���������݂����Ƃ��A�t�s��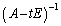 �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�s��̐���������������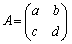 �ȂǂƂ��Ă͑�ςȂ��ƂɂȂ��Ă��܂��܂��BA�̂܂܍l���Ă������Ƃ���ł��B
�ȂǂƂ��Ă͑�ςȂ��ƂɂȂ��Ă��܂��܂��BA�̂܂܍l���Ă������Ƃ���ł��B
(1) 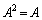 ���A
���A 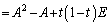
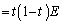 ......[��]
......[��]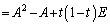
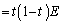 ......[��]
......[��]
(2) �s��A�ɑ��A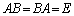 ���݂���B�����݂����B��A���t�s���ł��B
���݂���B�����݂����B��A���t�s���ł��B 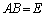 �@����@
�@����@���݂����s��B�����݂���Ɖ��肵�܂��B
�@���ӂɍ�����A��������ƁA
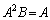 �@����A
�@����A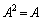 �Ƈ@���A
�Ƈ@���A����ćA���A
�ƂȂ�A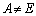 �ɔ����܂��B����āA�@���݂���B�͑��݂����AA�ɋt�s��͑��݂��܂���B
�ɔ����܂��B����āA�@���݂���B�͑��݂����AA�ɋt�s��͑��݂��܂���B 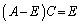 �@����B
�@����B���݂����s��C�����݂���Ɖ��肵�܂��B
�B���ӂɍ�����A��������ƁA
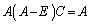 �@����C
�@����C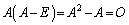
���A�C�̍��ӂ͗�s��ł����A�����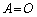 �ƂȂ�A
�ƂȂ�A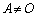 �ɔ����܂��B����āA�B���݂���C�͑��݂����A
�ɔ����܂��B����āA�B���݂���C�͑��݂����A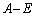 �ɋt�s��͑��݂��܂���B
�ɋt�s��͑��݂��܂���B
(3) 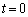 �܂���
�܂��� 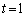 �̂Ƃ��́A(2)���A
�̂Ƃ��́A(2)���A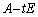 �͋t�s��������܂���B
�͋t�s��������܂���B 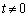 ����
���� 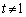 �̂Ƃ��́A(1)�̌��ʂ�
�̂Ƃ��́A(1)�̌��ʂ�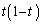 �Ŋ����āA
�Ŋ����āA���A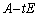 �͋t�s��
�͋t�s��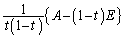 �������܂��B
�������܂��B
����āA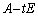 ���t�s��������߂��K�v�\�������́A
���t�s��������߂��K�v�\�������́A �g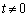 ����
���� 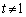 �h ......[��]
�h ......[��] 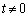 ����
���� 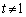 �̂Ƃ��A
�̂Ƃ��A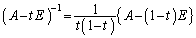 ......[��]
......[��]
�NjL�D���N�x�̓������������āA���̖�������������ʓI�ɍl���Ă݂܂��B
x�̑�����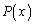 �𑽍���
�𑽍���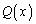 �Ŋ���v�Z�́A���̊���Z�Ɠ��l�ɂ��Ď��s�ł��܂�(�������̏��Z���Q��)�B
�Ŋ���v�Z�́A���̊���Z�Ɠ��l�ɂ��Ď��s�ł��܂�(�������̏��Z���Q��)�B
�������A�s��̑�����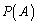 �𑽍���
�𑽍���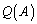 �Ŋ��邱�Ƃ͂ł��܂���B�s��ɂ͏��Z���Ȃ�����ł��B������
�Ŋ��邱�Ƃ͂ł��܂���B�s��ɂ͏��Z���Ȃ�����ł��B������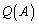 �Ŋ�������
�Ŋ�������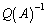 (���݂���ł���)�������邱�Ƃ��l���܂��B
(���݂���ł���)�������邱�Ƃ��l���܂��B
���̂��߂ɂ́A�s��̑�����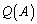 ���^����ꂽ�Ƃ��ɁA�ǂ�����ċt�s������߂邩�����ɂȂ�܂��B
���^����ꂽ�Ƃ��ɁA�ǂ�����ċt�s������߂邩�����ɂȂ�܂��B
A��2���̐����s��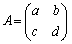 �ł���ꍇ(
�ł���ꍇ(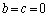 �ł͂Ȃ��C�܂�A
�ł͂Ȃ��C�܂�A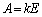 �̌`�ł͂Ȃ��Ƃ��܂�)�ɂ́A�n�~���g���E�P�[���[�̒藝�F
�̌`�ł͂Ȃ��Ƃ��܂�)�ɂ́A�n�~���g���E�P�[���[�̒藝�F
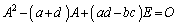 �@����@
�@����@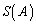 �ł����āA
�ł����āA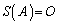 �ł�����̂��K�����݂��܂��B
�ł�����̂��K�����݂��܂��B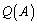 ��
��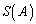 �Ŋ��邱�Ƃ��ł��Ȃ��̂ŁA����ɁA
�Ŋ��邱�Ƃ��ł��Ȃ��̂ŁA����ɁA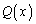 ��
��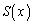 �Ŋ����ď���
�Ŋ����ď���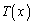 �C�]�肪
�C�]�肪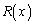 �ɂȂ�Ƃ��܂��B
�ɂȂ�Ƃ��܂��B
�ł��B�����ɁA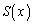 ��2�����Ȃ̂ŁA�]��
��2�����Ȃ̂ŁA�]��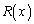 ��1�����ł���Ap�Cq�������Ƃ��āA
��1�����ł���Ap�Cq�������Ƃ��āA
�Ə������Ƃ��ł��܂��B�s��́A�����Z�Ȃ�ł���̂ŁAx��A�ɓ���ւ������F
���������܂��B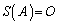 �Ȃ̂ŁA
�Ȃ̂ŁA
�Ȃ�A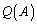 �������̑傫�ȑ������ł����Ă��AA��1�����ŕ\�����Ƃ��ł��܂�(���ꂪ�A�u���������v�ƌĂ��Z�I�ł�)�B����ƁA
�������̑傫�ȑ������ł����Ă��AA��1�����ŕ\�����Ƃ��ł��܂�(���ꂪ�A�u���������v�ƌĂ��Z�I�ł�)�B����ƁA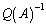 �����߂�Ƃ������Ƃ́A
�����߂�Ƃ������Ƃ́A
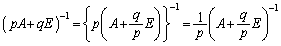 �@(
�@(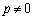 )�@����A
)�@����A
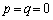 �̂Ƃ��́A
�̂Ƃ��́A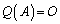 �ł�����
�ł�����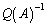 �͑��݂����A
�͑��݂����A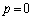 �C
�C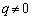 �̂Ƃ��́A
�̂Ƃ��́A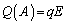 �ł�����
�ł�����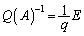 �ł��B
�ł��B
�A�ŁA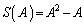 �C
�C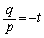 �Ƃ������̂��{��ł��B
�Ƃ������̂��{��ł��B
�@�𗘗p���āA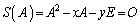 �C�܂�A
�C�܂�A
�Ə����Ă����Ƃ��܂��B�A��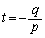 �Ƃ����āA�{��(1)�Ɠ��l�ɂ��āA
�Ƃ����āA�{��(1)�Ɠ��l�ɂ��āA
���ꂪE�̒萔�{�̌`�ɂȂ�Ƃ悢�̂ł����A���̂��߂ɂ́A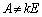 ���A
���A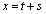 �C�܂�A
�C�܂�A
���K�v�ł��B���̂Ƃ��A
t��2��������(�s��A���ŗL������)�F
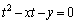 �@����B
�@����B
�ł���At ���ǂ�Ȏ����ł����Ă�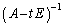 �����݂��܂����A
�����݂��܂����A
�̏ꍇ�ɂ́At ���B�̉��ȊO�̒l���Ƃ�Ƃ���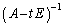 �����݂��܂��B
�����݂��܂��B
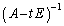 �����݂���Ƃ��ɂ́A
�����݂���Ƃ��ɂ́A
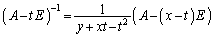 �@����C
�@����C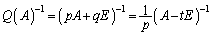
�Ⴆ�A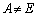 �C
�C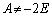 �C
�C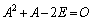 �@����D�@�����藧�Ƃ��ɁA
�@����D�@�����藧�Ƃ��ɁA
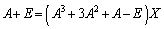 �@����E
�@����E
�ƇD���A
�C�ŁA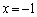 �C
�C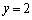 �C
�C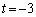 (
(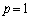 �C
�C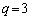 )�Ƃ��āA
)�Ƃ��āA
�E�̗��ӂɁA
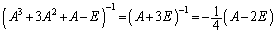 �@(��
�@(�� 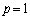 )
)
�ƂȂ�܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B