阪大理系数学'08年前期[3]
Nを2以上の自然数とする。
(1) 関数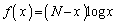
を
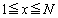の範囲で考える。このとき、曲線
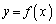は上に凸であり、関数
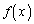は極大値を1つだけとる。このことを示せ。 (2) 自然数の列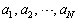
を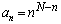 
(
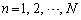)で定める。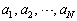
のうちで最大の値をMとし、
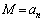となるnの個数をkとする。このとき
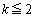であることを示せ。 (3) (2)で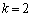
となるのは、Nが2のときだけであることを示せ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 (1)，(2)の流れから(3)で、頭が切り換えられるか、というところが勝負でしょう。
(
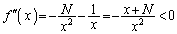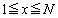)これより、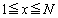
において、曲線
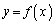は上に凸です(関数の凹凸を参照)。
また、導関数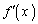
は単調減少です(関数の増減を参照)。 従って、xの方程式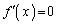
は、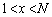
の範囲にただ1つの解を持ちます。この解をα とします。
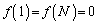より増減表は以下の通り。増減表より、関数
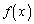は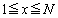
の範囲に極大値を1つだけとります。
(2) mを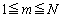
をみたす整数として、 です。関数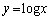
は単調増加な関数なので、
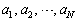のうちでMが最大値のとき、
，
，･･･，
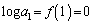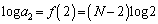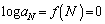のうちで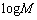
が最大値になります。 (1)のαが整数であれば、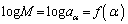
であり、 (1)のαが整数でなければ、(1)の増減表より、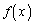
は、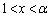
において単調増加、
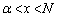において単調減少なので、
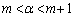をみたす整数mについて、 となるか、
となるか、
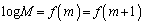(つまり、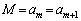
)となるか、このいずれかが起こります。いずれにしても、
以上より、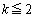
です。
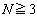のとき、(1)，(2)の流れで、関数
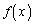の挙動を調べても、kの値に関する情報は得られません。そこで、整数の問題として考え、背理法を使うことにします。
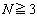のとき、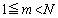
をみたす整数mについて、
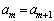，つまり、
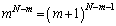･･･①が成り立つと仮定します。この両辺は、ともに整数の整数乗であって整数です。
また、mと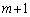
は互いに素(最大公約数が1)であるのに、①は、mが2以上の整数
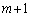の倍数であることを意味していて、不合理です。
よって、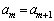
とした仮定は誤りです。即ち、(2)で
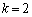となるのは、Nが2のときだけです。
注．もし、mと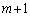
が互いに素でなく、2以上の整数をpとして、pを公約数を持つのであれば、
，
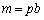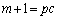をみたす整数b，cが存在します。 となり、1が2以上の整数pを約数にもつことになって不合理です。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
(∵ 
)
，または、
となる整数mについて、
です。
をみたす整数
が存在するとき、
，
をみたす整数
が存在するとき、
のとき、
，
より、
です。
