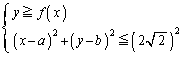埼玉大理数学'08年後期[4]
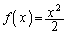 とする。以下の問いに答えよ。
とする。以下の問いに答えよ。
(1) 曲線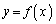 と点
と点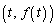 で接する半径
で接する半径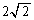 の円の中心の座標を
の円の中心の座標を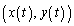 とする。ただし、
とする。ただし、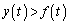 となるように円を選ぶものとする。
となるように円を選ぶものとする。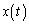 ,
,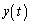 を求めよ。ここで、曲線
を求めよ。ここで、曲線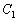 と曲線
と曲線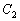 が点Pで接するとは、
が点Pで接するとは、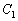 ,
,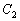 がともに点Pを通り、その点での接線が一致することである。
がともに点Pを通り、その点での接線が一致することである。 (2) 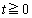 において
において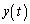 の最小値を与えるtの値を求めよ。また、そのときの円の中心の座標を求めよ。
の最小値を与えるtの値を求めよ。また、そのときの円の中心の座標を求めよ。 (3) (2)で求めた円の中心の座標を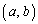 とするとき、連立不等式
とするとき、連立不等式 の表す領域を図示し、その面積を求めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 円と放物線が接する、という問題では、円の中心は法線上にある、というところから考えるのがよいでしょう。
 (1)
(1) 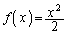
点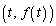 における接線の傾きはtです。
における接線の傾きはtです。
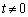 のとき、この点における法線(接線と垂直)の傾きは、
のとき、この点における法線(接線と垂直)の傾きは、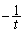 です(2直線の平行・垂直を参照)。
です(2直線の平行・垂直を参照)。
円の中心は法線上にあり、円の中心と接点との距離は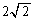 ですが、法線は、x方向に
ですが、法線は、x方向に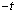 進むとy座標は1増える(直線の方程式を参照)ので、右図より、円の中心のx座標
進むとy座標は1増える(直線の方程式を参照)ので、右図より、円の中心のx座標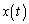 ,y座標
,y座標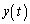 は、
は、
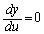 とすると、
とすると、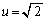 増減表より(関数の増減を参照)、
増減表より(関数の増減を参照)、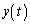 は
は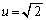 のときに最小で、このとき
のときに最小で、このとき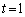 (
(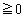 ) ......[答]このとき、
) ......[答]このとき、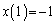 ,
,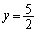 ,円の中心の座標は
,円の中心の座標は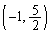 ......[答]
......[答]
(3) 円と放物線の位置関係が問題になります。
放物線上の点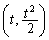 と円の中心
と円の中心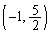 との距離の2乗と、円の半径
との距離の2乗と、円の半径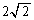 の2乗との大小関係を調べてみます。
の2乗との大小関係を調べてみます。 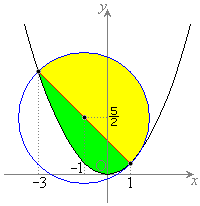 よって、
よって、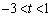 において
において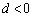 ,
,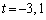 において
において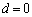 ,
,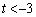 ,
,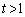 において
において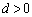
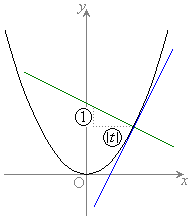
ということは、右図のように、放物線と円は、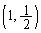 で接して
で接して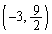 で交わり、放物線の
で交わり、放物線の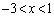 の部分は円の内部に、放物線の
の部分は円の内部に、放物線の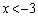 ,
,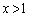 の部分は円の外部にある、ということです。
の部分は円の外部にある、ということです。
また、円の中心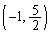 は、放物線と円の2つの共有点
は、放物線と円の2つの共有点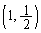 ,
,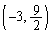 の中点です。ということは、2点
の中点です。ということは、2点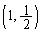 ,
,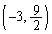 を結ぶ線分は、円の直径です。
を結ぶ線分は、円の直径です。
これより、連立不等式を満たすのは、放物線から上側であって円から内側の部分であり、右図の黄色着色部分と黄緑色着色部分を合わせた部分です。
黄色着色部分の面積は、半径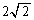 の円の面積の
の円の面積の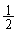 で、
で、黄緑色着色部分の面積は、
よって、求める面積は、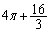 ......[答]
......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。