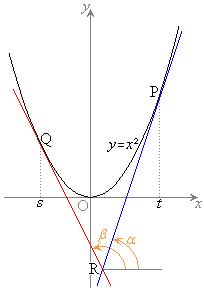
�}�g�吔�w'08�N[6]
������C�F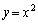 ��̈قȂ�2�_P
��̈قȂ�2�_P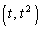 �CQ
�CQ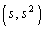 (
(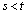 )�ɂ�����ڐ��̌�_��R
)�ɂ�����ڐ��̌�_��R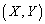 �Ƃ���B
�Ƃ���B
(1) X�CY��t�Cs��p���ĕ\���B
(2) �_P�CQ��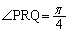 �����Ȃ���C����Ƃ��A�_R�͑o�Ȑ�������Ƃ������A���A���̑o�Ȑ��̕����������߂�B
�����Ȃ���C����Ƃ��A�_R�͑o�Ȑ�������Ƃ������A���A���̑o�Ȑ��̕����������߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(1)�Ŋ�{�Ώ̎����o�Ă���̂ŁA(2)��Ώ̎��ɂȂ�悤�ɕό`���čl���܂��B���������^�C�v�̖��ł́A�B�ꂽ�����ɒ��ӂ���K�v������̂ł����A���̖��ł́A���ӂ�Y��Ă��e���͂���܂���(�NjL���Q��)�B
(1) C�F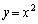
��������ƁA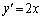 P
P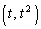 �ɂ�����ڐ��F
�ɂ�����ڐ��F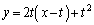
�� 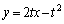 �@����@Q
�@����@Q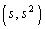 �ɂ�����ڐ��F
�ɂ�����ڐ��F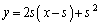
�� 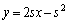 �@����A
�@����A
�@�C�A��A������ƁA 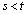 ���A
���A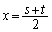
�@���A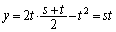
����āA�@�C�A�̌�_��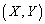 �Ƃ��āA
�Ƃ��āA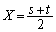 �C
�C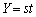 ......[��]
......[��]
(2) �������̐ڐ���x���ɐ����ɂȂ邱�Ƃ͂Ȃ��A�˂ɁA�@�C�A�̌X�������݂���̂ŁAtan���l���邱�Ƃɂ��܂��B
�@�C�A��x���̂Ȃ��p��α�Cβ �Ƃ��܂��B
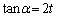 �C
�C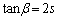
�ł��B�E�}���2�ڐ��̂Ȃ��p��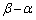 (
(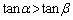 �ł����A
�ł����A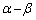 �ł͂Ȃ��̂Œ��ӂ��Ă�������)�ŁA���ꂪ
�ł͂Ȃ��̂Œ��ӂ��Ă�������)�ŁA���ꂪ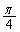 �ł��邱�Ƃ���A
�ł��邱�Ƃ���A �� 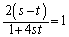 �@����B(1)�̌��ʂ�����A�B���A��{�Ώ̎�
�@����B(1)�̌��ʂ�����A�B���A��{�Ώ̎�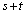 �C
�C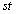 ��p���ĕ\���̂��낤�Ǝv���ł��傤�B�ł����A
��p���ĕ\���̂��낤�Ǝv���ł��傤�B�ł����A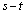 �͑Ώ̎��ł͂Ȃ��̂ŁA���̂܂܂ł͂��܂��s���܂���B�����ŁA2����l����ƁA
�͑Ώ̎��ł͂Ȃ��̂ŁA���̂܂܂ł͂��܂��s���܂���B�����ŁA2����l����ƁA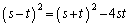 �͑Ώ̎��ł��B
�͑Ώ̎��ł��B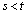 �Ȃ̂ŁA
�Ȃ̂ŁA �]���ćB�́A
�����ɁA(1)�̌��ʁA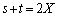 �C
�C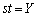 �������܂��B
�������܂��B ���������͐��Ȃ̂ŁA���̎����Ӗ������̂́A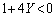 �C�܂�A
�C�܂�A �̂Ƃ��ł��B���̏����̂��Ƃɕ������2�悷��ƁA
��������ƁA
�� 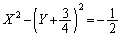 (�������A
(�������A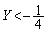 )������_R���o�Ȑ�����A���̑o�Ȑ��̕������́A
)������_R���o�Ȑ�����A���̑o�Ȑ��̕������́A 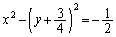 ......[��]
......[��]
�NjL�D��{�Ώ̎���p������ł͒��ӂ���ׂ����Ƃ�����܂��B�������B��Ă��邱�Ƃ�����̂ł��B��L�ŁA
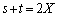 �C
�C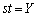
��2���ɂȂ�܂����As�Ct�͎����Ȃ̂ŁA����2���������͎������������A���ʎ���0�ł��B
�Ȃ̂ŁA���̖��ł́AR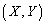 �͕�����
�͕�����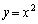 ���牺���ɂȂ���Ȃ�Ȃ��̂ł����A����ꂽ�o�Ȑ���
���牺���ɂȂ���Ȃ�Ȃ��̂ł����A����ꂽ�o�Ȑ���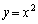 ���牺�ɂ���̂ŁA�B�ꂽ�������\�ɏo�Ă��邱�Ƃ͂���܂���B
���牺�ɂ���̂ŁA�B�ꂽ�������\�ɏo�Ă��邱�Ƃ͂���܂���B
�ł����A
�_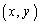 ���~
���~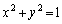 �̎�����Ƃ��A�_
�̎�����Ƃ��A�_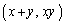 ���O�������߂�B
���O�������߂�B
�Ƃ������ł́A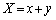 �C
�C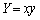 �Ƃ��āA
�Ƃ��āA
���A�O�Ղ̕������F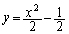 �������܂����A������
�������܂����A������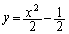 ��̓_�����ׂē��ɂȂ�킯�ł͂���܂���Bx�Cy�́At��2���������F
��̓_�����ׂē��ɂȂ�킯�ł͂���܂���Bx�Cy�́At��2���������F
��2���ŁAx�Cy�������A����2�����������������������Ƃ���A���ʎ��F
�ƂȂ�A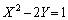 �ƍ��킹�āA
�ƍ��킹�āA
�� 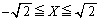
����āA�_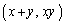 �̋O�Ղ́A�������F
�̋O�Ղ́A�������F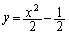 ��
��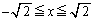 �̕����A�Ƃ������ƂɂȂ�܂��B
�̕����A�Ƃ������ƂɂȂ�܂��B
�gx�Cy�������h�Ƃ����Ƃ���ɏ������B��Ă��āA��蕶�Ɍ���Ă��Ȃ��̂Œ��ӂ��K�v�ł��B
�܂��A�{��ł́A2�ڐ��̂Ȃ��p��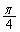 �ɂȂ��Ă��āA2�ڐ��̌�_�̋O�Ղ��o�Ȑ��ɂȂ�܂����A2�ڐ�����������̂ł���A�X���̐ρ�
�ɂȂ��Ă��āA2�ڐ��̌�_�̋O�Ղ��o�Ȑ��ɂȂ�܂����A2�ڐ�����������̂ł���A�X���̐ρ�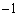 (2�����̕��s�E�������Q��)���A
(2�����̕��s�E�������Q��)���A
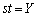 ���A
���A
�ƂȂ��āA2�ڐ��̌�_�̋O�Ղ�������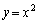 �̏���
�̏���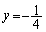 �ɂȂ�܂��B
�ɂȂ�܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B