�������b��吔�w'09�N[2]
(1) �^����ꂽ�s��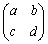 (������
(������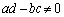 )�ɑ��āA������
)�ɑ��āA������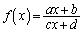 ����܂�B
����܂�B (i) ��̍s��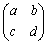 (������
(������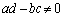 )�C
)�C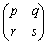 (������
(������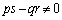 )�Œ�܂镪���������ꂼ��
)�Œ�܂镪���������ꂼ��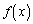 �C
�C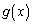 �Ƃ���B�܂��A��̍s��̐ς�
�Ƃ���B�܂��A��̍s��̐ς� �Ƃ���Ƃ��A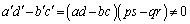 �ł��邱�Ƃ��������Ă���B
�ł��邱�Ƃ��������Ă���B
���̖��肪���藧���Ƃ��ؖ�����B 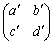 �Œ�܂镪�����́A������
�Œ�܂镪�����́A������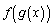 �ł���B
�ł���B(2) �Q����
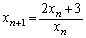 �@(
�@(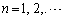 )�@����@
)�@����@�ƁA����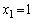 �ŗ^����ꂽ����
�ŗ^����ꂽ����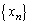 �̑�
�̑�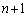 ��
��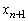 ��n��p���ĕ\�������B
��n��p���ĕ\�������B
�s��A��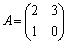 �Ƃ��A
�Ƃ��A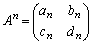 �@(
�@(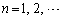 )�Ƃ���B
)�Ƃ���B (i) �Q�����@�ŗ^����ꂽ����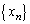 �ɂ��āA
�ɂ��āA �����藧���Ƃ��A���w�I�A�[�@�ɂ��ؖ�����B
(ii) 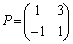 �Ƃ���B
�Ƃ���B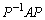 �����߁A�����
�����߁A�����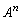 ��n��p���ĕ\���B
��n��p���ĕ\���B (iii) ����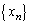 �̑�
�̑�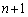 ��
��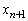 (
(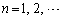 )��n��p���ĕ\���B
)��n��p���ĕ\���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�����^�C�v���Q�������s����p���Ĉ������Ƃ������ł��B
�Ȃ��A�Q�����̋Z�I�A�s��̗ݏ����Q�Ƃ��Ă��������B
(1) ��̍s��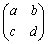 �C
�C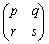 �Œ�܂��
�Œ�܂��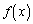 �C
�C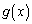 �́A
�́A 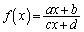 �C
�C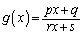
�ł��B
�Œ�܂��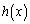 �́A
�́A �ł��B
����āA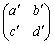 �Œ�܂镪�����́A������
�Œ�܂镪�����́A������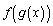 �ł��B
�ł��B
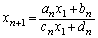 �@����A
�@����A�������܂��B
(�T) 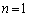 �̂Ƃ��A
�̂Ƃ��A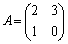 ���A
���A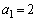 �C
�C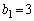 �C
�C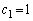 �C
�C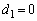 �Ȃ̂ŁA�@���A
�Ȃ̂ŁA�@���A ����āA�A���������܂��B
(�U) 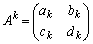 �Ƃ��āA
�Ƃ��āA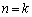 �̂Ƃ��ɇA�������A�܂�A
�̂Ƃ��ɇA�������A�܂�A 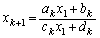 �@����B
�@����B����������Ɖ��肵�܂��B
�Œ�܂镪�����́A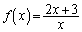 �C
�C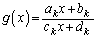 �Ƃ��āA(1)���A
�Ƃ��āA(1)���A �ł��B�Q�����@���A
�܂��A�B���A
�Ə����܂����A
���A�A�́A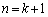 �̂Ƃ��ɂ��������܂��B
�̂Ƃ��ɂ��������܂��B (�T)�C(�U)���A�Q�����@�ŗ^����ꂽ����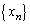 �ɂ��āA
�ɂ��āA �����藧���܂��B�@(�ؖ��I)
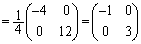 ......[��]
......[��]�Ƃ���ŁA
���A
���ӂɍ�����P�C�E����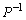 �������āA
�������āA 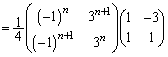
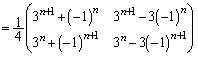 ......[��]
......[��](iii) (ii)���A
�� 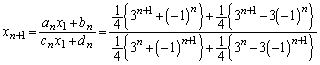
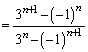 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 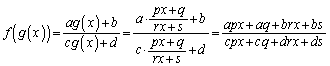
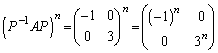
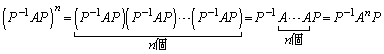
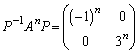
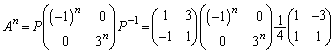
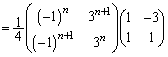
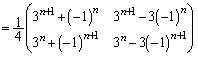 ......[��]
......[��]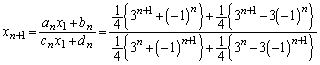
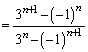 ......[��]
......[��]