���嗝�H���w'09�N[4]
a�Cb�͎����ŁA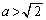 �Ƃ���Bxy���ʏ�̓_
�Ƃ���Bxy���ʏ�̓_ ����Ȑ�
����Ȑ�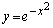 �ɐڐ����������Ƃ��ł��邽�߂̏��������߂����B
�ɐڐ����������Ƃ��ł��邽�߂̏��������߂����B
(1) �Ȑ�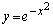 ��̓_
��̓_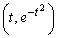 �ɂ�����ڐ��̌X����y�ؕЂ����߂�B
�ɂ�����ڐ��̌X����y�ؕЂ����߂�B (2) 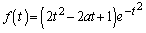 �Ƃ����B
�Ƃ����B (a) ��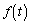 �̑����ׁA�ɒl�����߂�B
�̑����ׁA�ɒl�����߂�B (b) 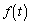 �̂Ƃ蓾��l�͈̔͂����߂�B�K�v�Ȃ�A
�̂Ƃ蓾��l�͈̔͂����߂�B�K�v�Ȃ�A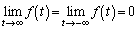 ��p���Ă悢�B
��p���Ă悢�B (3) �_ ����Ȑ�
����Ȑ�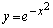 �ɐڐ����������Ƃ��ł��邽�߂̏�����a�Cb��p�������ŕ\���B
�ɐڐ����������Ƃ��ł��邽�߂̏�����a�Cb��p�������ŕ\���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�m�[�q���g���ƌ��������ł����A�U���ʂ�ɐi�߂Ύ肪�~�܂邱�Ƃ͂Ȃ��Ǝv���܂��B
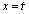 �ɂ������ڐ��̌X���́A
�ɂ������ڐ��̌X���́A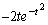 ......[��]�_
......[��]�_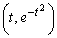 �ɂ�����ڐ��̕������́A
�ɂ�����ڐ��̕������́A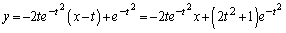 �@����@
�@����@����y�ؕЂ́A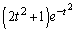 ......[��]
......[��]
(2)(a) 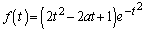
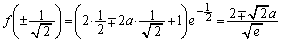 (��������)
(��������)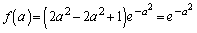
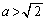 �̂Ƃ��A��
�̂Ƃ��A��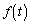 �̑����͈ȉ��̕\�̒ʂ�(���̑������Q��)�B
�̑����͈ȉ��̕\�̒ʂ�(���̑������Q��)�B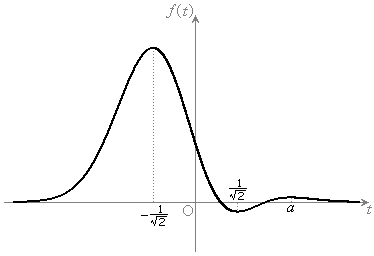 �����\���A
�����\���A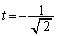 �̂Ƃ��ɑ�l
�̂Ƃ��ɑ�l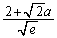 �C
�C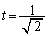 �̂Ƃ��ɏ��l
�̂Ƃ��ɏ��l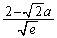 �C
�C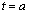 �̂Ƃ��ɑ�l
�̂Ƃ��ɑ�l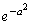 ......[��]
......[��](b) ��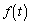 �̃O���t�́A
�̃O���t�́A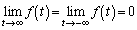 ���l�����ĉE�}�̂悤�ɂȂ�܂��B�O���t���A
���l�����ĉE�}�̂悤�ɂȂ�܂��B�O���t���A �͈̔͂́A
�͈̔͂́A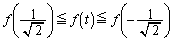 ���A
���A 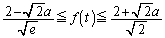 ......[��]
......[��]
(3) �ڐ��@���_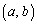 ��ʂ�Ƃ��A
��ʂ�Ƃ��A 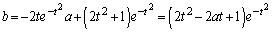 �@����A
�@����A�����t�Ɋւ���������ƌ���ƁA���̕��������������Ƃ��ɓ_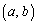 ��ʂ�ڐ����������Ƃ��ł��܂��B
��ʂ�ڐ����������Ƃ��ł��܂��B
���̉E�ӂ�t�������Ƃ���Ƃ���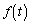 �ŁA���̂Ƃ蓾��l��(2)(b)�ŋ��߂��ʂ�Ȃ̂ŁA
�ŁA���̂Ƃ蓾��l��(2)(b)�ŋ��߂��ʂ�Ȃ̂ŁA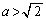 �̂Ƃ��A�������A���������A�܂�A�_
�̂Ƃ��A�������A���������A�܂�A�_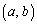 ����Ȑ�
����Ȑ�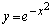 �ɐڐ����������Ƃ��ł��邽�߂̏�����(�����@�̕������ւ̉��p���Q��)�A
�ɐڐ����������Ƃ��ł��邽�߂̏�����(�����@�̕������ւ̉��p���Q��)�A 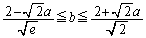 ......[��]
......[��] �NjL�D
�NjL�D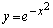 ��2���������ƁA
��2���������ƁA������A�Ȑ�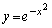 �́A
�́A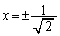 �̂Ƃ�����ϋȓ_������̂ł����A�ϋȓ_�ɂ�����ڐ��́A
�̂Ƃ�����ϋȓ_������̂ł����A�ϋȓ_�ɂ�����ڐ��́A (3)�̌��ʂ́A
(i) 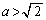 �̂Ƃ��A
�̂Ƃ��A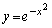 �ɐڐ���������̂́A����
�ɐڐ���������̂́A����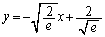 �����Œ���
�����Œ���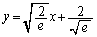 ���牺�̗̈���̓_����ł���B
���牺�̗̈���̓_����ł���B �Ƃ������Ƃ��Ӗ����Ă��܂��B���l�ɁA
(ii) 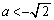 �̂Ƃ��A����
�̂Ƃ��A����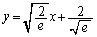 �����Œ���
�����Œ���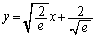 ���牺�̗̈���̓_����
���牺�̗̈���̓_����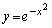 �ɐڐ����������Ƃ��ł��܂��B
�ɐڐ����������Ƃ��ł��܂��B (iii) 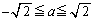 �ɂ����ẮA
�ɂ����ẮA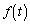 ��
��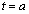 �ōŏ��l
�ōŏ��l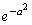 ���Ƃ�悤�ɂȂ�A
���Ƃ�悤�ɂȂ�A �Ȑ�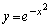 �����Œ���
�����Œ���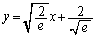 ���牺�̗̈���̓_����
���牺�̗̈���̓_����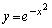 �ɐڐ����������Ƃ��ł��܂��B
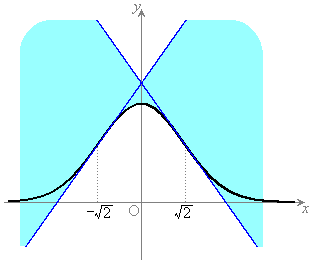
�ɐڐ����������Ƃ��ł��܂��B ���ǁA�Ȑ�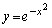 (���F����)�ɐڐ����������Ƃ��ł���_�͉E�}���F���F��(���E�����܂�)�ł��B�F�א��͒���
(���F����)�ɐڐ����������Ƃ��ł���_�͉E�}���F���F��(���E�����܂�)�ł��B�F�א��͒���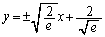 (�ϋȓ_�ɂ�����ڐ�)�ł��B
(�ϋȓ_�ɂ�����ڐ�)�ł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B