���H�吔�w'09�N[2]
�ȉ~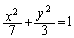 �����_�𒆐S�ɔ����v���Ɋp
�����_�𒆐S�ɔ����v���Ɋp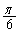 ������]���ē�����Ȑ���C�Ƃ���B
������]���ē�����Ȑ���C�Ƃ���B
(1) �Ȑ�C�̕����������߂�B
(2) ����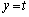 ��C�Ƌ��L�_�����悤�Ȏ���t�͈̔͂����߂�B
��C�Ƌ��L�_�����悤�Ȏ���t�͈̔͂����߂�B (3) ���ׂĂ̒��_��C��ɂ���A1�ӂ�x���ɕ��s�ȎO�p�`�̖ʐς̍ő�l�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�߂̑ȉ~���l����̂ł����A�ȉ~���߂ɂ��Ȃ��Ă��A����߂ɂ��đȉ~�����̂܂܂ōl���邱�Ƃ��ł��܂��B
�ȉ~�̕������F
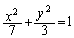 �@����@
�@����@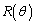 �́A
�́A
�ł�(1���ϊ�(����2)���Q��)�B�_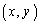 �� �A
�� �A
���{���ƁA
�ɗ��܂��B
(1) ���߂�Ȑ�C�̕�������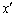 �C
�C �̊W���ɂȂ�܂����A���m�̎���x�Cy�̊W���@�Ȃ̂ŁA
�̊W���ɂȂ�܂����A���m�̎���x�Cy�̊W���@�Ȃ̂ŁA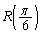 �̋t�ϊ�
�̋t�ϊ� �ɂ��Ax�Cy��
�ɂ��Ax�Cy��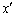 �C
�C ��p���āA
��p���āA �ƕ\���A������@�ɑ������悤�ɂ��܂��B����ƁA
�������āA
�� 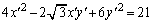 �Ȑ��̕������́A
�Ȑ��̕������́A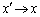 �C
�C �Ə��������āA
�Ə��������āA 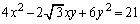 ......[��]�@����A
......[��]�@����A
(2) �{��ł͉�]��̕����������߂Ă���̂ŁA(1)�̌��ʂ𗘗p���ĉ��Ă��ǂ��̂ł����A��ʓI�ɂ́A�ȉ~���v���� ��]����̂ł͂Ȃ��A�ȉ~�����̂܂܂ɂ��āA����
��]����̂ł͂Ȃ��A�ȉ~�����̂܂܂ɂ��āA����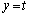 �̕���
�̕��� ��]���čl��������֗��ł��B
��]���čl��������֗��ł��B ����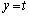 ��x���ɕ��s�Ȓ����ŌX��0�ł����A���_�𒆐S�ɔ����v����
��x���ɕ��s�Ȓ����ŌX��0�ł����A���_�𒆐S�ɔ����v����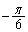 ��]����ƁA�X����
��]����ƁA�X����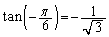 �ɂȂ�܂��B
�ɂȂ�܂��B
���������̕��������A  �@����B
�@����B�Ƃ����ƁA���_�Ƃ̋����� �Ȃ̂ŁA
�Ȃ̂ŁA �B��c�ƇC��t�̕����͈�v���܂��B
�����B��y�ؕ�c���ω����A�ȉ~�@�Ƌ��L�_�����Ƃ��A���̌��E�ɂ����āA�����B���ȉ~�ɐڂ��܂��B�ړ_�� �Ƃ��đȉ~�@�̐ڐ��́A
�Ƃ��đȉ~�@�̐ڐ��́A ���̌X���� �̏ꍇ�������āA
�̏ꍇ�������āA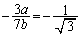
�� 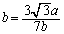 �ړ_�͇@��̓_�Ȃ̂ŁA
�ړ_�͇@��̓_�Ȃ̂ŁA �� 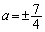 �C
�C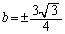 (��������)
(��������)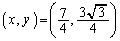 �̂Ƃ��A�B�C�C���A
�̂Ƃ��A�B�C�C���A 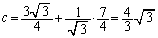 �C
�C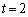 �@����D
�@����D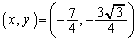 �̂Ƃ��A�B�C�C���A
�̂Ƃ��A�B�C�C���A �C
�C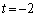 �@����E
�@����Et���D�ƇE�̊Ԃ̒l���Ƃ�Ƃ��ɁA����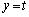 ��C�Ƌ��L�_�������܂��B
��C�Ƌ��L�_�������܂��B
�� 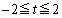 ......[��]�ʉ��D�@�ƇB��A�����A
......[��]�ʉ��D�@�ƇB��A�����A �� 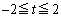 �Ƃ��邱�Ƃ��ł��܂��B
�Ƃ��邱�Ƃ��ł��܂��B
�܂��A�A�� �Ƃ��āA
�Ƃ��āA 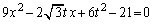 ���ʎ��F
���ʎ��F
�Ƃ��邱�Ƃ��ł��܂��B
(3) (2)�Ɠ��l�ɑȉ~����]����̂ł͂Ȃ��A���� �̕�����]���čl���܂��B
�̕�����]���čl���܂��B ��蕶��x���ɕ��s�ȕӂ�����Ă��钼����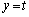 �Ƃ���ƁA��������_�𒆐S�ɔ����v����
�Ƃ���ƁA��������_�𒆐S�ɔ����v����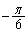 ��]����ƁA�B�C�C���A
��]����ƁA�B�C�C���A 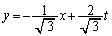 �@����G
�@����G����1���_���ȉ~����Ƃ��A�O�p�`�̖ʐς��ő�ƂȂ�̂́A���̒��_�ɂ�����ڐ����G�ɕ��s�A�܂�ڐ��̌X���� �ɂȂ�Ƃ��ł��B�X��
�ɂȂ�Ƃ��ł��B�X��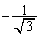 �̐ڐ���2�{����܂����A���̂����A�O�p�`�̖ʐς��傫���̂́A�D�C�E���A����1���_���A
�̐ڐ���2�{����܂����A���̂����A�O�p�`�̖ʐς��傫���̂́A�D�C�E���A����1���_���A �̂Ƃ��ɂ�
�̂Ƃ��ɂ� �C
�C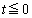 �̂Ƃ��ɂ�
�̂Ƃ��ɂ� �̂Ƃ��ł��B
�̂Ƃ��ł��B
�ȉ~�@��x���Ɋւ��đΏ̂Ȃ̂ŁA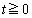 �̕��������l���邱�Ƃɂ��܂��B�O�p�`�̍���h�́A
�̕��������l���邱�Ƃɂ��܂��B�O�p�`�̍���h�́A �ƇG�Ƃ̋����Ƃ��āA
�ƇG�Ƃ̋����Ƃ��āA �O�p�`�̒�ӂ̒���d�́A�ȉ~�@�ƒ����B�Ƃ̌�_��x���W�̍���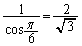 �����������̂ɂȂ�܂��B�F��2���̍��́A
�����������̂ɂȂ�܂��B�F��2���̍��́A ��ӂ̒����́A
����āA�O�p�`�̖ʐ�S�́A
 �@(
�@(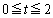 )
)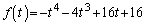 �Ƃ����ƁA
�Ƃ����ƁA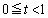 �ɂ�����
�ɂ�����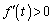 �C
�C �ɂ�����
�ɂ����� ���A
���A ��
��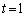 �̂Ƃ��ɍő�(���̑������Q��)�ŁAS�̍ő�l�́A
�̂Ƃ��ɍő�(���̑������Q��)�ŁAS�̍ő�l�́A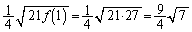 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 
