���R�嗝�n���w'09�N[2]
2�~2�s��A��B���A����
�����Ă���Ƃ���B�������AO�͗�s���\���B���̂Ƃ��ȉ��̖₢(1)�C(2)�ɓ�����B�����K�v�ł���A�s��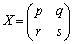 �ɑ���
�ɑ���
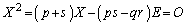 �@���(��)
�@���(��)
(1) ���鐔α�Cβ�ɑ���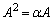 �C
�C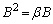 �ƂȂ邱�Ƃ������B
�ƂȂ邱�Ƃ������B (2) (1)�ɂ�����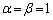 �̂Ƃ��A
�̂Ƃ��A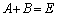 �������B
�������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�s��̑Ίp�a���l�^�ɂ������ł��B
(2)�ł́A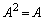 �C
�C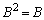 �����s�o�Ă��܂����A������ˉe�q(�������́A�[�ˉe�q)�ƌ����܂��B�X�y�N�g�������ɏo�Ă���s��ŁA�C�ӂ̃x�N�g�����ŗL�x�N�g���̕����ւ̐�������铭���������Ă��܂��B�ȉ��ŁA�s�ɂ��ẮA�t�s�����Q�Ƃ��Ă��������B
�����s�o�Ă��܂����A������ˉe�q(�������́A�[�ˉe�q)�ƌ����܂��B�X�y�N�g�������ɏo�Ă���s��ŁA�C�ӂ̃x�N�g�����ŗL�x�N�g���̕����ւ̐�������铭���������Ă��܂��B�ȉ��ŁA�s�ɂ��ẮA�t�s�����Q�Ƃ��Ă��������B
��蕶�̏����F
�s��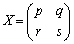 �ɑ��āA�s��X��
�ɑ��āA�s��X��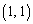 ����p��
����p��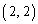 ����q�̘a(�Ίp�a�ƌ����܂�)��
����q�̘a(�Ίp�a�ƌ����܂�)��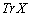 �Ə������Ƃɂ��܂��B�܂�A
�Ə������Ƃɂ��܂��B�܂�A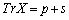 �ł��B
�ł��B
X�̍s��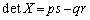 �Ȃ̂ŁA(��)���A
�Ȃ̂ŁA(��)���A
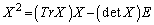 �@����A
�@����A
(1) 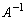 �����݂���Ɖ��肵�āA�����@��
�����݂���Ɖ��肵�āA�����@��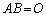 �̍�����
�̍�����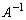 ��������ƁA
��������ƁA 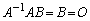 �ƂȂ��ď����@�ɔ�����̂ŁA
�ƂȂ��ď����@�ɔ�����̂ŁA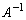 �͑��݂��܂���(�w���@���Q��)�B
�͑��݂��܂���(�w���@���Q��)�B
���l�ɁA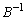 �����݂���Ɖ��肵�āA�����@��
�����݂���Ɖ��肵�āA�����@��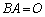 �̍�����
�̍�����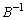 ��������ƁA
��������ƁA
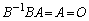 �ƂȂ��ď����@�ɔ�����̂ŁA
�ƂȂ��ď����@�ɔ�����̂ŁA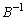 �����݂��܂���B
�����݂��܂���B
�� 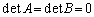 ����āA�s��A�C�s��B�ɇA��K�p����ƁA
����āA�s��A�C�s��B�ɇA��K�p����ƁA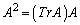 �C
�C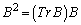
(2) 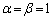 ��(1)���A
��(1)���A 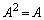 �C
�C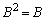
������A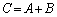 �Ƃ����ƁA�����@��p���āA
�Ƃ����ƁA�����@��p���āA 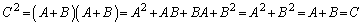 �@����B
�@����B�܂��A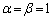 �́A
�́A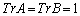 �ł��邱�Ƃ��Ӗ����܂��B
�ł��邱�Ƃ��Ӗ����܂��B
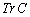 �͍s��C��
�͍s��C��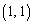 ������
������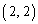 �����̘a�A�܂�A
�����̘a�A�܂�A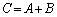 ��
��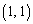 ������
������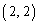 �����̘a�ł����A����́A�s��A��
�����̘a�ł����A����́A�s��A��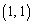 ������
������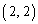 �����̘a�ƁA�s��B��
�����̘a�ƁA�s��B��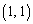 ������
������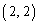 �����̘a�A�Ƃ̘a�ł����āA
�����̘a�A�Ƃ̘a�ł����āA �A���A�s��C�ɂ��āA
�ƂȂ�܂����A�B���A
����āA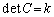 �Ƃ����āA
�Ƃ����āA 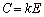 �@����C
�@����C�Ə������Ƃ��ł��܂��B�ĂчB���A
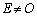 �Ȃ̂ŁA
�Ȃ̂ŁA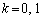
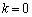 �́A�C���
�́A�C���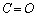 �ƂȂ��āA
�ƂȂ��āA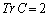 �ɂ͂Ȃ蓾�Ȃ��̂ŁA�s�K�B
�ɂ͂Ȃ蓾�Ȃ��̂ŁA�s�K�B
����āA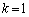
�C���A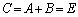
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B