�X�y�N�g�������@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���̍��ڂ́A1���ϊ��A�ŗL�l�E�ŗL�x�N�g���A�n�~���g���E�P�[���[�̒藝�A�s��̑Ίp�����Q�Ƃ��Ă��������B
n�������s��A���قȂ�ŗL�l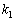 �C
�C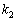 �C����C
�C����C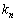 �Ƃ���ɑΉ�����ŗL�x�N�g��
�Ƃ���ɑΉ�����ŗL�x�N�g��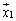 �C
�C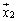 �C����C
�C����C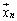 (�����̌ŗL�x�N�g����1���Ɨ��ł�)�����Ƃ��܂��B���̂Ƃ��A
(�����̌ŗL�x�N�g����1���Ɨ��ł�)�����Ƃ��܂��B���̂Ƃ��A
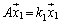 �C
�C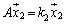 �C����C
�C����C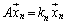 �@����@
�@����@
�����́A�s��A������ŗL�̕���(�ŗL�x�N�g���ɕ��s�ȕ���)�������Ă��āA���̕����̃x�N�g���ɍs��A��������ƒ������ς�邾���A�ƌ������Ƃ��Ӗ����Ă��܂��B
n������Ԓ��̔C�ӂ̃x�N�g���F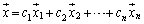 (
(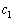 �C
�C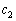 �C����C
�C����C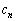 �͔C�ӂ̎���)�ɍs��A��������ƁA�@��p���āA
�͔C�ӂ̎���)�ɍs��A��������ƁA�@��p���āA
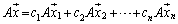
�@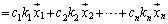
�ƂȂ�܂����A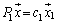 �C
�C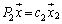 �C����C
�C����C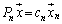 �@���(��)�@�̂悤�Ȉ�A�̍s��
�@���(��)�@�̂悤�Ȉ�A�̍s��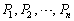 ��{���Ă��āA
��{���Ă��āA
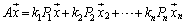
�@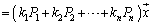 �@����A
�@����A
�̂悤�ɏ������Ƃ��l���Ă݂܂��B
�A���C�ӂ̃x�N�g��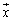 �ɂ��Đ��藧�ĂA�P�����̏������A
�ɂ��Đ��藧�ĂA�P�����̏������A
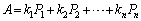 �@����B
�@����B
���������܂��B
(��)�̂悤�Ȑ����́A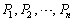 �����ꂼ��A�C�ӂ̃x�N�g��
�����ꂼ��A�C�ӂ̃x�N�g��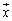 ��
��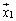 �̕��������A
�̕��������A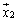 �̕��������A����C
�̕��������A����C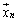 �̕������������o���悤�ȍs��ł��邱�Ƃ��Ӗ����Ă��܂��B���̂悤�Ȑ��������s��A
�̕������������o���悤�ȍs��ł��邱�Ƃ��Ӗ����Ă��܂��B���̂悤�Ȑ��������s��A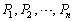 ���A�ˉe�q�ƌĂт܂��B
���A�ˉe�q�ƌĂт܂��B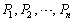 ���\��1���ϊ����A
���\��1���ϊ����A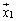 �C
�C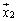 �C����C
�C����C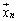 �̕����ւ̎ˉe�ƌ����܂��B
�̕����ւ̎ˉe�ƌ����܂��B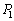 �ł���A
�ł���A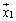 �ȊO�̂��ׂĂ̌ŗL�x�N�g���ƕ��s�ȕ�������
�ȊO�̂��ׂĂ̌ŗL�x�N�g���ƕ��s�ȕ�������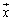 �Ɍ��ĂāA
�Ɍ��ĂāA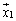 �̕����ւ̉e����邱�Ƃɑ������܂��B
�̕����ւ̉e����邱�Ƃɑ������܂��B
�Ⴆ�A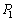 ���ˉe�q�ł��邽�߂ɂ́A
���ˉe�q�ł��邽�߂ɂ́A
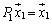 �C
�C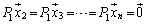 �@����C
�@����C
�ł���A����(��)�����������̂ŁA���̃E�F�u�T�C�g�ł́A�C��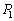 ���ˉe�q�ł��邽�߂̏����ƍl���邱�Ƃɂ��܂��B
���ˉe�q�ł��邽�߂̏����ƍl���邱�Ƃɂ��܂��B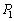 �����߂邽�߂ɁA�C��1�ɂ܂Ƃ߂ď����ƁA
�����߂邽�߂ɁA�C��1�ɂ܂Ƃ߂ď����ƁA
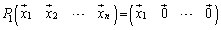
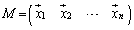 �́A
�́A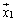 �C
�C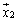 �C����C
�C����C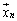 ��1���Ɨ��Ȃ̂ŁA����(
��1���Ɨ��Ȃ̂ŁA����(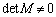 )�ł���A�t�s��
)�ł���A�t�s��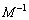 �������܂��B�㎮���ӂ̉E����
�������܂��B�㎮���ӂ̉E����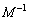 ��������ƁA
��������ƁA
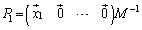
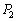 �C����C
�C����C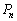 �ɂ��Ă��A�S�����l�ɂ��āA
�ɂ��Ă��A�S�����l�ɂ��āA
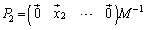
�@�����
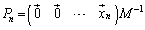
���āA�������ē���ꂽ�ˉe�q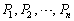 �����ɂǂ̂悤�Ȑ����������ׂĂ݂܂��B
�����ɂǂ̂悤�Ȑ����������ׂĂ݂܂��B
�ˉe�q�����ׂĉ������킹��ƁA
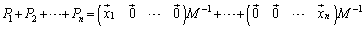
�@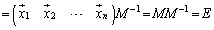
���A�P�ʍs��ɂȂ�܂��B
�܂��A�����C���A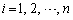 �C
�C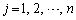 �C
�C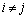 �̂Ƃ��A
�̂Ƃ��A
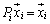 �C
�C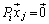 �C
�C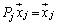 �C
�C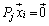
����āA�C�ӂ̃x�N�g��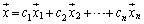 �ɑ��āA
�ɑ��āA
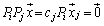 �C
�C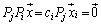
���A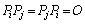 (��s��)�ł��B
(��s��)�ł��B
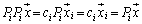
���A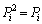 �ł��B
�ł��B
�t�ɁA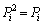 �����s����Ƃ��ɁA�C�ӂ̃x�N�g��
�����s����Ƃ��ɁA�C�ӂ̃x�N�g��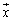 ��
��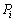 ���������Ƃ��ɁA����x�N�g��
���������Ƃ��ɁA����x�N�g��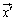 ���Ƃ���
���Ƃ���
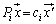 �@(
�@(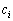 �͎���)
�͎���)
�ɂȂ����Ƃ���ƁA
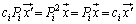
����āA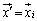 �Ƃ���A
�Ƃ���A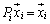 �Ə�����̂ŁA
�Ə�����̂ŁA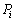 ��
��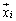 �̕����ւ̎ˉe�q�ł��B
�̕����ւ̎ˉe�q�ł��B
�܂��A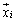 ���܂�1���Ɨ��ȃx�N�g���̑g
���܂�1���Ɨ��ȃx�N�g���̑g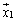 �C
�C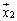 �C����C
�C����C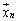 (i��1����n�̂ǂꂩ)�ɂ��āA
(i��1����n�̂ǂꂩ)�ɂ��āA
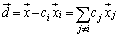 �Ƃ����ƁA
�Ƃ����ƁA
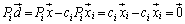
�܂�A
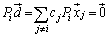
���C�ӂ̎���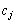 (
(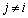 )�ɂ��Đ��藧�̂ŁA�P�����̏������A
)�ɂ��Đ��藧�̂ŁA�P�����̏������A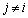 �ƂȂ�j�ɂ��āA
�ƂȂ�j�ɂ��āA
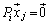
�ƂȂ��āA�C�������܂��B�]���āA
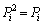 (
(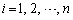 )
)
���A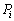 ���ˉe�q�ł��邽�߂̕K�v�\�������ł��B
���ˉe�q�ł��邽�߂̕K�v�\�������ł��B
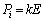 (k�F����)�Ƃ����`�����Ă���ƁA
(k�F����)�Ƃ����`�����Ă���ƁA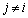 �ƂȂ�j�ɂ��āA
�ƂȂ�j�ɂ��āA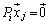 �ƂȂ蓾�Ȃ��̂ŁA
�ƂȂ蓾�Ȃ��̂ŁA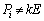 �ł��B
�ł��B
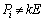 �ł���A
�ł���A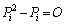 �ƃn�~���g���E�P�[���[�̒藝���A�ŗL������
�ƃn�~���g���E�P�[���[�̒藝���A�ŗL������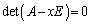 ��������������ƁA
��������������ƁA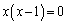 ���o�Ă��āA�ˉe�q
���o�Ă��āA�ˉe�q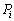 �́A�ŗL�l0�C1�������Ƃ��킩��܂��B
�́A�ŗL�l0�C1�������Ƃ��킩��܂��B
�ŗL�l1�ɑ���ŗL�x�N�g�����A��L�ɏo�Ă����A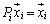 ���A
���A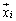 �ł��B
�ł��B
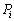 ���ŗL�l0�����Ƃ������Ƃ͂ǂ��������Ƃ��ƌ����ƁA
���ŗL�l0�����Ƃ������Ƃ͂ǂ��������Ƃ��ƌ����ƁA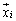 �ȊO�̕����̐����͂��ׂďk�߂�0�ɂ��Ă��܂��A�Ƃ������Ƃł��B
�ȊO�̕����̐����͂��ׂďk�߂�0�ɂ��Ă��܂��A�Ƃ������Ƃł��B
�B��p���邱�Ƃɂ��A�s��̗ݏ�̌v�Z��e�Ղɍs�����Ƃ��ł���̂ł����A�ʏ�́A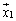 �ւ́u�ˉe�v�ƌ����ꍇ�A
�ւ́u�ˉe�v�ƌ����ꍇ�A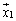 �Ɛ����ȕ���������ĂĂł���e�A�܂�u���ˉe�v�̂��Ƃ��w���܂��B�܂��A�ˉe�q�ɂ́A�C�ȊO�ɂ����������܂��B
�Ɛ����ȕ���������ĂĂł���e�A�܂�u���ˉe�v�̂��Ƃ��w���܂��B�܂��A�ˉe�q�ɂ́A�C�ȊO�ɂ����������܂��B
���ˉe���l����ꍇ�ɂ́A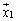 �C
�C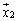 �C����C
�C����C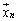 �����K�������ƂȂ�ꍇ(���݂ɐ����ŁA���A���ꂼ��̑傫����1)���l����̂ŁA��L�́A
�����K�������ƂȂ�ꍇ(���݂ɐ����ŁA���A���ꂼ��̑傫����1)���l����̂ŁA��L�́A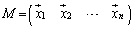 �́A�����s��ɂȂ�܂��B
�́A�����s��ɂȂ�܂��B
�@��1�ɂ܂Ƃ߂ď����ƁA
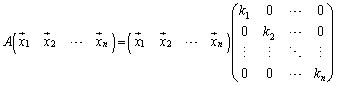 ���A
���A
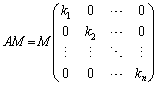 �Ə����āA������
�Ə����āA������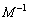 ��������ƁA
��������ƁA
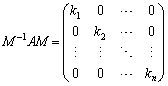
�ƂȂ��āA�s��A��Ίp���ł��܂����A����̓]�u�s����l����ƁA
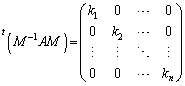
M�͒����s���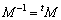 �����̂ŁA�����̉E�ӂ����������Ƃ��A
�����̂ŁA�����̉E�ӂ����������Ƃ��A
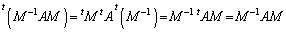
�]���āA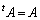 �����s��(�Ίp�����Ɋւ��āA�E��ƍ����ɑΏ̂ɐ��������Ԃ̂ŁA�Ώ̍s��ƌ����܂�)���A�����s��ɂ���đΊp���ł��邱�Ƃ��킩��܂��B
�����s��(�Ίp�����Ɋւ��āA�E��ƍ����ɑΏ̂ɐ��������Ԃ̂ŁA�Ώ̍s��ƌ����܂�)���A�����s��ɂ���đΊp���ł��邱�Ƃ��킩��܂��B
���̂Ƃ��A�Ⴆ�A�ˉe�q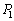 �ɂ��Ă��A
�ɂ��Ă��A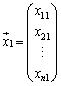 �Ƃ��āA
�Ƃ��āA
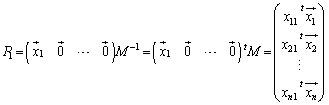
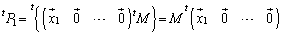
�@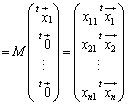 ���(�v�Z�����G�ł��B�������Ă��˂��ɏ����Ċm���߂Ă�������)�A
���(�v�Z�����G�ł��B�������Ă��˂��ɏ����Ċm���߂Ă�������)�A
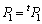 �����藧�̂ŁA
�����藧�̂ŁA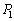 ��(
��(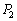 �C����C
�C����C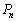 �����l��)�Ώ̍s��ɂȂ�܂��B
�����l��)�Ώ̍s��ɂȂ�܂��B
�������āA�Ώ̍s��A�ɂ��āA�Ώ̍s��ł���ˉe�q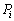 ��p���āA�B�̂悤�ɏ������Ƃ��ł��܂��B�����Ώ̍s��A�̃X�y�N�g�������ƌ����܂��B
��p���āA�B�̂悤�ɏ������Ƃ��ł��܂��B�����Ώ̍s��A�̃X�y�N�g�������ƌ����܂��B
�ł����AA���Ώ̍s��łȂ��Ă��A�قȂ�ŗL�l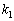 �C
�C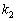 �C����C
�C����C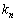 �����ĂA�S�����^�̇B�������藧�̂ŁA���̃E�F�u�T�C�g�ł́AA���Ώ̍s��łȂ��ꍇ�ɂ��Ă��A�B�����s��A�̃X�y�N�g�������ƌĂԂ��Ƃɂ��܂�(�]���āA���ˉe�łȂ��Ă��A�C�C���邢�́A
�����ĂA�S�����^�̇B�������藧�̂ŁA���̃E�F�u�T�C�g�ł́AA���Ώ̍s��łȂ��ꍇ�ɂ��Ă��A�B�����s��A�̃X�y�N�g�������ƌĂԂ��Ƃɂ��܂�(�]���āA���ˉe�łȂ��Ă��A�C�C���邢�́A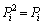 �����藧�����Ŏˉe�q�ƌĂԂ��Ƃɂ��܂�)�B
�����藧�����Ŏˉe�q�ƌĂԂ��Ƃɂ��܂�)�B
(�X�y�N�g������(����2)�ւÂ�)
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 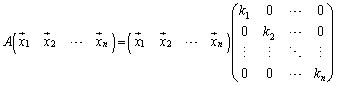 ���A
���A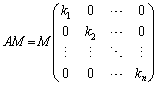 �Ə����āA������
�Ə����āA������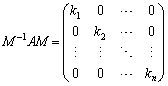
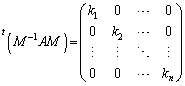
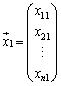 �Ƃ��āA
�Ƃ��āA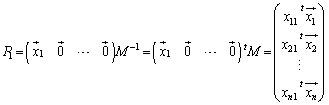
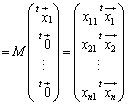 ���(�v�Z�����G�ł��B�������Ă��˂��ɏ����Ċm���߂Ă�������)�A
���(�v�Z�����G�ł��B�������Ă��˂��ɏ����Ċm���߂Ă�������)�A