��嗝�n���w'09�N�O��[1]
������C�F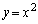 ��̓_
��̓_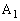
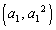 �C
�C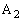
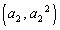 �C
�C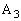
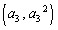 �C��� ���A
�C��� ���A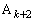 (
(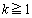 )�ɂ�����C�̐ڐ�������
)�ɂ�����C�̐ڐ�������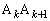 �ɕ��s�ł���悤�ɂƂ�B�������A
�ɕ��s�ł���悤�ɂƂ�B�������A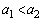 �Ƃ���B�O�p�`
�Ƃ���B�O�p�`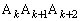 �̖ʐς�
�̖ʐς�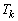 �Ƃ��A����
�Ƃ��A����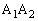 ��C�ň͂܂ꂽ�����̖ʐς�S�Ƃ���B���̂Ƃ����̖₢�ɓ�����B
��C�ň͂܂ꂽ�����̖ʐς�S�Ƃ���B���̂Ƃ����̖₢�ɓ�����B
(1) 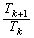 �����߂�B
�����߂�B (2) 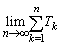 ��S��p���ĕ\���B
��S��p���ĕ\���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@������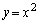 �̈قȂ�3�_
�̈قȂ�3�_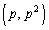 �C
�C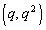 �C
�C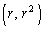 �_�Ƃ���O�p�`�̖ʐς�
�_�Ƃ���O�p�`�̖ʐς�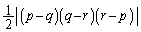 �ƂȂ邱�Ƃ𗘗p���܂��B
�ƂȂ邱�Ƃ𗘗p���܂��B
(1) ����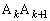 ��������Ƃ������Ƃ́A
��������Ƃ������Ƃ́A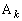 �C
�C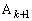 ����v���邱�Ƃ͂Ȃ��A�Ƃ������Ƃł��B�܂�A
����v���邱�Ƃ͂Ȃ��A�Ƃ������Ƃł��B�܂�A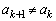
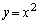 �C
�C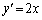
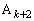 �ɂ�����ڐ�������
�ɂ�����ڐ�������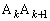 �ɕ��s�ɂȂ邱�Ƃ���A
�ɕ��s�ɂȂ邱�Ƃ���A
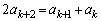 �@(�ڐ��Ɣ����W�����Q��)��
�@(�ڐ��Ɣ����W�����Q��)�� 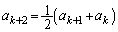 �@����@
�@����@�@���A
�� 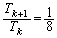 ......[��]������A
......[��]������A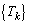 �́A����
�́A����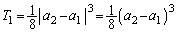 �C����
�C����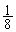 �����䐔���ł��B
�����䐔���ł��B
(2) ����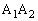 �̕�������
�̕�������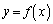 �Ƃ��āA
�Ƃ��āA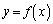 ��
��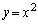 ��A�������Ƃ��̉���
��A�������Ƃ��̉���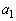 �C
�C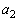 �ł��B������A
�ł��B������A 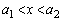 �ɂ����Ă�
�ɂ����Ă�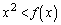 �Ȃ̂ŁA
�Ȃ̂ŁA������A����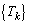 �̏���
�̏���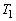 �́A
�́A �������䋉��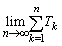 �́A����
�́A����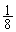 ��
��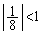 �Ȃ̂ŁA�������Ęa�������܂��B
�Ȃ̂ŁA�������Ęa�������܂��B
�a�́A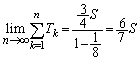 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B