��嗝�n���w'09�N�O��[2]
k��2�ȏ�̎��R���Ƃ���B�u1�v�Ə����ꂽ�J�[�h��1���A�u2�v�Ə����ꂽ�J�[�h��2���A����A�uk�v�Ə����ꂽ�J�[�h��k������B���̂����̋����������ꂽ�J�[�h�̖�����M�C��������ꂽ�J�[�h�̖�����N�ŕ\���B����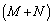 ���̃J�[�h���悭������1�������o���A�����ɏ����ꂽ�����L�^���Ă��Ƃɖ߂��Ƃ��������n��J��Ԃ��B�L�^���ꂽn�̐��̘a�������ƂȂ�m����
���̃J�[�h���悭������1�������o���A�����ɏ����ꂽ�����L�^���Ă��Ƃɖ߂��Ƃ��������n��J��Ԃ��B�L�^���ꂽn�̐��̘a�������ƂȂ�m����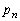 �Ƃ���B���̖₢�ɓ�����B
�Ƃ���B���̖₢�ɓ�����B
(1)  ��
�� ��M�CN�ŕ\���B
��M�CN�ŕ\���B (2)  ��
�� �CM�CN�ŕ\���B
�CM�CN�ŕ\���B (3) 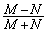 ��k�ŕ\���B
��k�ŕ\���B (4)  ��n��k�ŕ\���B
��n��k�ŕ\���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@M�CN��k�̋��ŕ�����܂����An�Ɉˑ�����킯�ł͂Ȃ��̂ŁA�W���I��2���ԑQ�����̖��ł��B
(1) 1��̑���ŋ����������m����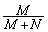 �C��������m����
�C��������m����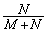 �ł��B����āA
�ł��B����āA  ......[��]
......[��]2��̑���ŋL�^���ꂽn�̐��̘a�������ƂȂ�̂́A1��ڂ�2��ڂ������ł���Ƃ���1��ڂ�2��ڂ���ł���Ƃ��ŁA
(2)  ��ڂ܂ł̑����
��ڂ܂ł̑���� �̐��̘a�������ƂȂ�̂́An��ڂ܂ł̑����n�̐��̘a������(�m��
�̐��̘a�������ƂȂ�̂́An��ڂ܂ł̑����n�̐��̘a������(�m��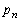 )�ł�����
)�ł�����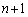 ��ڂ̑���ŋ����̃J�[�h�����o���Ƃ��ƁAn��ڂ܂ł̑����n�̐��̘a���(�m��
��ڂ̑���ŋ����̃J�[�h�����o���Ƃ��ƁAn��ڂ܂ł̑����n�̐��̘a���(�m��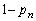 )�ł�����
)�ł�����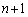 ��ڂ̑���Ŋ�̃J�[�h�����o���Ƃ��ŁA
��ڂ̑���Ŋ�̃J�[�h�����o���Ƃ��ŁA ��  ......[��]�@����@
......[��]�@����@
(3)�Ek����̂Ƃ��A
�Ek�������̂Ƃ��A
(4) �@�ɂ����āA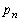 �C
�C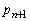 ��α�ɒu�������āA
��α�ɒu�������āA 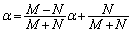 �@����A
�@����A����������āA
�@�|�A���A
������A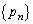 �́A����
�́A����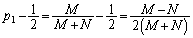 �C����
�C����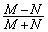 �����䐔���ł��B
�����䐔���ł��B �� 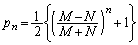
(3)�̌��ʂ��Ak����̂Ƃ��A ......[��]
......[��]
k�������̂Ƃ��A ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B