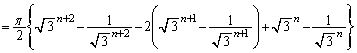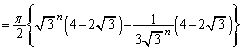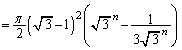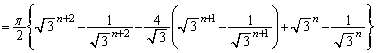東京理科大理(数理)数学'09年[4]
対数を自然対数とする。数列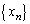 (
(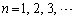 )を
)を
により定める。ただし、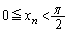 とする。次の問いに答えよ。
とする。次の問いに答えよ。
(1) 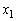 を求めよ。
を求めよ。 (2)  を求めよ。
を求めよ。 (3) 曲線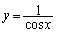 とx軸および2直線
とx軸および2直線 ,
, で囲まれた図形をx軸のまわりに1回転してできる回転体の体積を
で囲まれた図形をx軸のまわりに1回転してできる回転体の体積を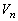 とする。
とする。 を求めよ。
を求めよ。 (4) (3)で求めた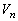 に対して、
に対して、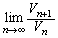 を求めよ。
を求めよ。 (5) (3)で求めた に対して、不等式
に対して、不等式 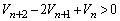 (
( )
)が成り立つことを証明せよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 数学Ⅲの範囲全般にわたる計算問題です。
(1) 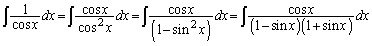
これより、
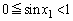 より
より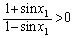 となるので、
となるので、∴ 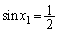
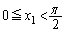 より、
より、  ......[答]
......[答]
(2) ①より、
 より
より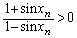 となるので、
となるので、∴ 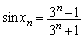 ......[答]
......[答]
(2)の結果を用いて、
∴  ......[答]
......[答]
(4) 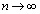 のとき、
のとき、 ∴  ......[答]
......[答]
(5) 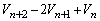
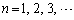 のとき、
のとき、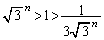 より、
より、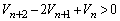 (証明終)
(証明終)この2次方程式を特性方程式とする3項間漸化式は、
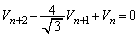 ・・・②
・・・②です。そこで、②が成立するかどうか確かめてみると、
となるので、②が成立します。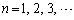 に対して、
に対して、 より
より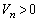 ですが、
ですが、 より、
より、 となるので、
となるので、
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 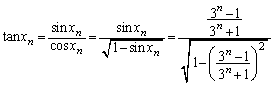

 ......[答]
......[答]