�����吔�w'10�N[2]
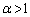 �Ƃ���B
�Ƃ���B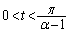 �ƂȂ�t�ɑ��āAxy���ʏ�̓_P
�ƂȂ�t�ɑ��āAxy���ʏ�̓_P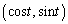 �Ɠ_Q
�Ɠ_Q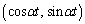 ��ʂ钼����
��ʂ钼����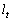 �Ƃ���B���̖�ɓ�����B
�Ƃ���B���̖�ɓ�����B
��1�@����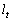 �̕�������
�̕������� ��2�@�s��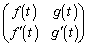 �͋t�s��������Ƃ������B
�͋t�s��������Ƃ������B ��3�@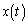 �C
�C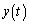 ��
�� �������̂Ƃ��A�_R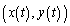 ���`���Ȑ���C�Ƃ���B���̂Ƃ��A�_R�͒���
���`���Ȑ���C�Ƃ���B���̂Ƃ��A�_R�͒���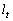 ��ɂ���A�Ȑ�C�̓_R�ɂ�����ڐ���
��ɂ���A�Ȑ�C�̓_R�ɂ�����ڐ���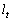 �ƈ�v���邱�Ƃ������B
�ƈ�v���邱�Ƃ������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�s�����g���ċL�q���ꂽ���ł����A�����I�ɂ͎O�p���̌v�Z���ł��B
��1�@����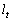 �́A�_P
�́A�_P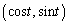 ��ʂ�̂ŁA
��ʂ�̂ŁA 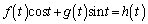 �@����@
�@����@����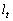 �́A�_Q
�́A�_Q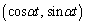 ��ʂ�̂ŁA
��ʂ�̂ŁA 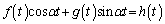 �@����A
�@����A�@�~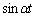 �|�A�~
�|�A�~ ���A
���A �́A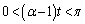 ���A
���A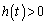 �C����āA�B���A
�C����āA�B���A 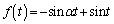 ......[��]
......[��]�@�~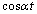 �|�A�~
�|�A�~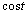 ���A
���A 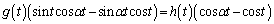
 ......[��]
......[��]
��2�@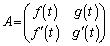 �Ƃ��āA
�Ƃ��āA 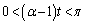 ���A
���A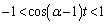
����āA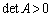 �Ȃ̂ŁAA���t�s���������܂��B
�Ȃ̂ŁAA���t�s���������܂��B
��3�@�^�����A
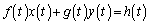 �@����C
�@����C
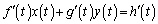 �@����D
�@����D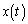 �C
�C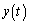 �́A�C�C�D��A�������Ƃ��̉��ł����A�C�͒���
�́A�C�C�D��A�������Ƃ��̉��ł����A�C�͒���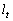 �̕������ɂق��Ȃ�Ȃ��̂ŁA�_R
�̕������ɂق��Ȃ�Ȃ��̂ŁA�_R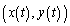 �͒���
�͒���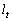 ��̓_�ł��B
��̓_�ł��B
�C�C�D��A��������ƁA��2���A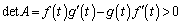 �Ȃ̂ŁA
�Ȃ̂ŁA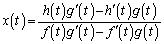 �C
�C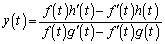
�ƂȂ�܂����A������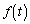 �C
�C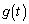 �C
�C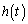 �̋�̓I�Ȍ`�������A�}��ϐ��\�����ꂽ���̔��������F
�̋�̓I�Ȍ`�������A�}��ϐ��\�����ꂽ���̔��������F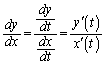 ��p���Đڐ��̕����������߂�̂ł͑�ςł��B
��p���Đڐ��̕����������߂�̂ł͑�ςł��B
�����ŁA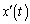 �C
�C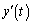 ���o�Ă���悤�ɁA�C��������Ă݂܂��B
���o�Ă���悤�ɁA�C��������Ă݂܂��B 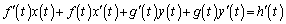 �@����E
�@����E�E�|�D���A
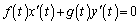 �@����F
�@����F�����ŁA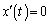 �ƂȂ�\��������̂ō���܂��B
�ƂȂ�\��������̂ō���܂��B 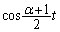 ��
��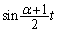 �͓����Ƀ[���ɂȂ邱�Ƃ͂Ȃ��̂ŁA
�͓����Ƀ[���ɂȂ邱�Ƃ͂Ȃ��̂ŁA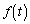 ��
��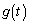 �������Ƀ[���ɂȂ邱�Ƃ͂���܂���B
�������Ƀ[���ɂȂ邱�Ƃ͂���܂���B���D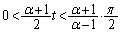 �Ȃ̂�
�Ȃ̂�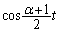 �C�܂�
�C�܂�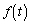 �́A
�́A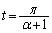 (
(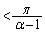 )�ɂ����ă[���ɂȂ�܂��B
)�ɂ����ă[���ɂȂ�܂��B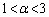 �̂Ƃ��A
�̂Ƃ��A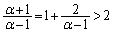 �ƂȂ�̂ŁA
�ƂȂ�̂ŁA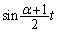 �A�܂�
�A�܂�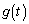 �́A���Ȃ��Ƃ�
�́A���Ȃ��Ƃ�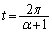 �ɂ����ă[���ɂȂ�܂��B
�ɂ����ă[���ɂȂ�܂��B �ȉ��A�_R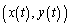 �ɂ�����ڐ���̓_��
�ɂ�����ڐ���̓_��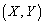 �Ƃ��āA�ڐ��̕��������l���܂��B
�Ƃ��āA�ڐ��̕��������l���܂��B
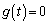 �̂Ƃ��A
�̂Ƃ��A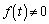 �ŁA�F���
�ŁA�F���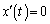
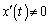 �̂Ƃ�(
�̂Ƃ�(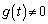 )�ɂ́A�F���A
)�ɂ́A�F���A 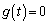 ����t��
����t��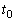 �Ƃ���ƁA
�Ƃ���ƁA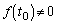 �Ȃ̂ŁA
�Ȃ̂ŁA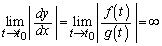 �C�Ƃ������Ƃ́A
�C�Ƃ������Ƃ́A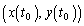 �ɂ�����ڐ��́Ax���ɐ����ŁA
�ɂ�����ڐ��́Ax���ɐ����ŁA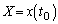 �ƂȂ�܂��B
�ƂȂ�܂��B
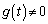 �̂Ƃ��A�ڐ��́A
�̂Ƃ��A�ڐ��́A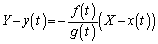
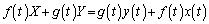 �@����G
�@����G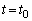 �̂Ƃ��A
�̂Ƃ��A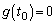 �C
�C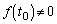 ���A
���A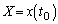 �ƂȂ�̂ŁA�G�́A
�ƂȂ�̂ŁA�G�́A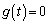 �̏ꍇ���܂�ł��܂��B�G�́A�C��p����ƁA
�̏ꍇ���܂�ł��܂��B�G�́A�C��p����ƁA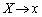 �C
�C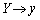 �Ƃ��āA
�Ƃ��āA����āA�Ȑ�C�̓_R�ɂ�����ڐ���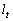 �ƈ�v���܂��B
�ƈ�v���܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B  ��p���Đڐ��̕����������߂�̂ł͑�ςł��B
��p���Đڐ��̕����������߂�̂ł͑�ςł��B