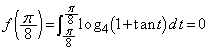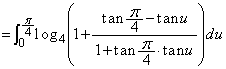�F�{��㐔�w'10�N[3]
��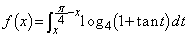 (
(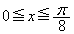 )�ɂ��āA�ȉ��̖₢�ɓ�����B
)�ɂ��āA�ȉ��̖₢�ɓ�����B
(��1)  �̓���
�̓���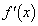 �����߂�B
�����߂�B (��2) 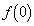 �̒l�����߂�B
�̒l�����߂�B (��3) ����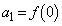 �C
�C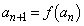 (
(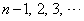 )�ɂ���Ē�܂鐔��
)�ɂ���Ē�܂鐔��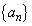 �̈�ʍ�
�̈�ʍ�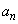 �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(��2)�ł͒�ϕ������s���Ȃ��Ă�(��1)�𗘗p���ĉł��Ă��܂��܂����A��ϕ������s����Ȃ�A�����ϕ��̂悤�ȕ��͋C�ɂȂ�܂��B
(��2) (��1)���A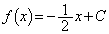 �@����@
�@����@ 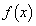 �̒�ϕ��̏�[�Ɖ��[�����A�ƁA�����ƁA
�̒�ϕ��̏�[�Ɖ��[�����A�ƁA�����ƁA�ʉ��D��ϕ������s���Ă݂܂��B
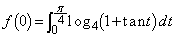 �@����A
�@����A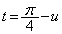 �Ƃ����ƁA
�Ƃ����ƁA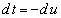 �Ct�F
�Ct�F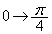 �̂Ƃ��Au�F
�̂Ƃ��Au�F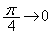 �@(�u���ϕ����Q��)
�@(�u���ϕ����Q��)�� 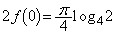 ��
�� 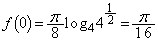
(��3) (��2)���A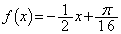
�B�|�C���A
�� 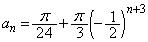 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B