���s�{����吔�w'10�N[3]
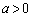 �Ƃ��A���W���ʏ��2�̋Ȑ�
�Ƃ��A���W���ʏ��2�̋Ȑ� �F
�F �C
�C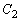 �F
�F ���l����B
���l����B
(1)  �ł���Ƃ��A
�ł���Ƃ��A ��
��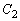 �͋��L�_�������Ȃ����Ƃ������B
�͋��L�_�������Ȃ����Ƃ������B (2)  �ł���Ƃ��A
�ł���Ƃ��A ��
��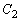 �̋��L�_�̍��W��a��p���ĕ\���B
�̋��L�_�̍��W��a��p���ĕ\���B (3) (2)�̏ꍇ�ŁA���L�_��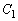 �̕ϋȓ_�ł���Ƃ��Aa�̒l�����߂�B
�̕ϋȓ_�ł���Ƃ��Aa�̒l�����߂�B (4) a��(3)�̒l�̂Ƃ��A ��
��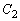 �ň͂܂ꂽ������y���̂܂���1��]�����Ăł��闧�̂̑̐ς����߂�B
�ň͂܂ꂽ������y���̂܂���1��]�����Ăł��闧�̂̑̐ς����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�ʓ|�Ȕ��ς̌v�Z���ł��B�T�d�Ɍv�Z���邵������܂���B
(1) 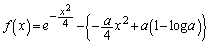
�Ƃ����܂��B
 �@����@
�@����@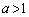 �ł���Ax���S�������Ƃ�Ƃ�
�ł���Ax���S�������Ƃ�Ƃ�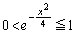 �Ȃ̂ŁA�@��������x�͂���܂���B�܂��A
�Ȃ̂ŁA�@��������x�͂���܂���B�܂��A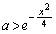 �ł��B�]���āA
�ł��B�]���āA �Ȃ�
�Ȃ�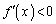 ��
��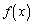 �͌����A
�͌����A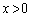 �Ȃ�
�Ȃ�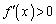 ��
��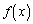 �͑����A����āA
�͑����A����āA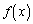 ��
��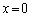 �ɂ����čŏ��l
�ɂ����čŏ��l ���Ƃ�܂�(���̑������Q��)�B
���Ƃ�܂�(���̑������Q��)�B�Ƃ����ƁA
 �@(��
�@(��  )
)��� �͒P�������ŁA
�͒P�������ŁA �ɂ����āA
�ɂ����āA
(2)  �̂Ƃ��A(1)��
�̂Ƃ��A(1)�� �ɂ��āA
�ɂ��āA �@ �� 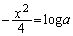 ��
�� 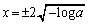 �@(
�@(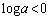 �ɒ���)�@����A
�ɒ���)�@����A ���A �Ƃ��āA�@��2��
�Ƃ��āA�@��2��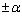 �������܂��B
�������܂��B
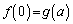 �́A
�́A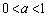 �ɂ����āA
�ɂ����āA ���
���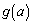 �͌������A
�͌������A �܂��A ���A
���A �����\���A������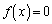 �́A������
�́A������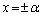 �������܂��B�܂��A
�������܂��B�܂��A �ɂ�����
�ɂ�����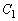 ��
��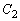 ���ڂ��邱�Ƃ��킩��܂��B
���ڂ��邱�Ƃ��킩��܂��B
 �̂Ƃ��A�A���A
�̂Ƃ��A�A���A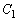 ��y���W��a�ł��B
��y���W��a�ł��B
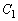 ��
��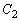 �̋��L�_�̍��W�́A
�̋��L�_�̍��W�́A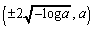 ......[��]
......[��]
(3) 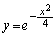
 �Ƃ���ƁA
�Ƃ���ƁA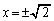
���̂Ƃ��A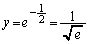 (2)��苤�L�_��y���W��a�Ȃ̂ŁA���L�_��
(2)��苤�L�_��y���W��a�Ȃ̂ŁA���L�_��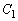 ���ϋȓ_�ł���Ƃ��A
���ϋȓ_�ł���Ƃ��A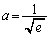 ......[��]���̂Ƃ��A�ϋȓ_�̍��W��
......[��]���̂Ƃ��A�ϋȓ_�̍��W�� �ƂȂ�܂��B
�ƂȂ�܂��B
�܂��A �C
�C ��y���Ƃ̌�_�́A
��y���Ƃ̌�_�́A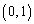 �C
�C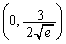 (
(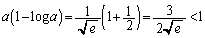 )�ł��B
)�ł��B
(4) (2)�C(3)���A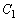 ��
�� �͕ϋȓ_�Őڂ��Ă��āA�ړ_�ȊO�ł�
�͕ϋȓ_�Őڂ��Ă��āA�ړ_�ȊO�ł� ��
�� �̏�ɂ���܂��B
�̏�ɂ���܂��B �Ƃ��āA �C
�C �ɂ����āA
�ɂ����āA �C
�C �Ȃ̂ŁA
�Ȃ̂ŁA ��
�� �ň͂܂ꂽ������y���̂܂���1��]�����Ăł��闧�̂̑̐�V�́A
�ň͂܂ꂽ������y���̂܂���1��]�����Ăł��闧�̂̑̐�V�́A
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B