���s�{����吔�w'10�N[1]
O�����_�Ƃ�����W���ʏ�̑ȉ~C�F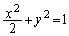 ���l����B
���l����B
�_P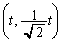 (�������A
(�������A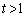 )��ʂ�ȉ~C��2�̐ڐ���
)��ʂ�ȉ~C��2�̐ڐ���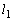 �C
�C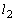 �Ƃ��A�����Ƒȉ~�Ƃ̐ړ_�����ꂼ��Q�CR�Ƃ���B�_Q��ʂ�
�Ƃ��A�����Ƒȉ~�Ƃ̐ړ_�����ꂼ��Q�CR�Ƃ���B�_Q��ʂ�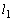 �ƒ������钼����
�ƒ������钼����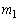 �Ƃ��A�_R��ʂ�
�Ƃ��A�_R��ʂ�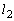 �ƒ������钼����
�ƒ������钼����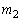 �Ƃ���B����
�Ƃ���B����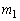 ��
��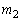 �̌�_��S�Ƃ���B�������AQ��x���W��R��x���W���傫���Ƃ���B
�̌�_��S�Ƃ���B�������AQ��x���W��R��x���W���傫���Ƃ���B
(1) 2�_Q�CR�̍��W��t ��p���ĕ\���B
(2) �_S�̍��W��t ��p���ĕ\���B
(3) t ��1���傫�������S�̂��Ƃ��A�_S�̋O�Ղ����߂�B
(4) 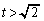 �ł���Ƃ��A��OPS�̖ʐς�
�ł���Ƃ��A��OPS�̖ʐς�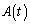 �Ƃ���B
�Ƃ���B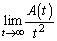 �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�܂Ƃ��ɘr�����Ōv�Z���悤�Ƃ���Ǝ��E�����Ȃ��Ȃ�܂��B�ǂ�����Čv�Z���邩�A�Ƃ������Ƃ�����Ă�����ł��B�Ȃ��A�ȉ~���Q�Ƃ��Ă��������B
(1) �_P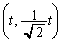 ��ʂ�������
��ʂ�������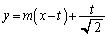 �Ƃ�����
�Ƃ�����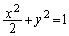 �ƘA�����Ă����Ɛ��܂������ƂɂȂ�܂��B�X��m�������o�����ɁA���ځA�ړ_�̍��W�����߂�悤�ɂ��܂��B
�ƘA�����Ă����Ɛ��܂������ƂɂȂ�܂��B�X��m�������o�����ɁA���ځA�ړ_�̍��W�����߂�悤�ɂ��܂��B �ړ_Q�CR�̍��W��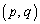 �Ƃ����܂��B�ړ_�͑ȉ~C��̓_�Ȃ̂ŁA
�Ƃ����܂��B�ړ_�͑ȉ~C��̓_�Ȃ̂ŁA 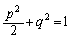 �@����@
�@����@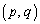 �ɂ�����ȉ~C�̐ڐ��́A
�ɂ�����ȉ~C�̐ڐ��́A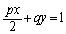 �@����A
�@����A�_P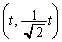 ��ʂ�̂ŁA
��ʂ�̂ŁA 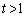 �Ȃ̂ŁA
�Ȃ̂ŁA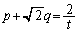
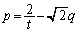 �@����B
�@����B���@�ɑ�����āA
�������āA
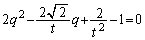 �@����C
�@����C�� 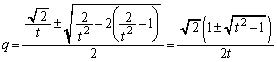 �B���A
�B���A Q��x���W��R��x���W���傫���̂ŁA
Q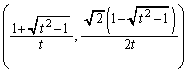 �CR
�CR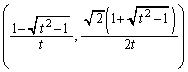 ......[��]
......[��]
(2) ������(1)�̌��ʂ����̂܂g���ĘA���������������̂ł͑�ςł��BQ�CR�̍��W���悭���āA�v�Z���H�v���܂��BQ��x���W��R��y���W��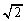 �{�AR��x���W��Q��y���W��
�{�AR��x���W��Q��y���W�� �{�ɂȂ��Ă��邱�Ƃɒ��Ⴕ�܂��B�Ώ̐�������̂ŁA�Ώ̎��̗��p���l���܂��B
�{�ɂȂ��Ă��邱�Ƃɒ��Ⴕ�܂��B�Ώ̐�������̂ŁA�Ώ̎��̗��p���l���܂��B �C��2���A�܂�AQ�CR��y���W��α�Cβ �Ƃ����܂��B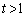 ���
���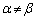 �ł��B
�ł��B
�C�ɂ����āA���ƌW���̊W���A 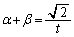 �C
�C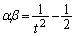 �@����D
�@����D�����ŁA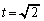 �̂Ƃ���
�̂Ƃ���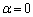 �ƂȂ邱�Ƃɒ��ӂ��܂��B
�ƂȂ邱�Ƃɒ��ӂ��܂��B (i) 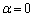 �C�܂�
�C�܂�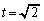 �̂Ƃ��AQ
�̂Ƃ��AQ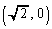 �CR
�CR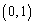 �ł��BQ�ɂ�����ڐ�
�ł��BQ�ɂ�����ڐ�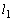 ��
��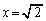 �CR�ɂ�����ڐ�
�CR�ɂ�����ڐ�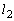 ��
��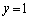 �CQ�ɂ�����@��
�CQ�ɂ�����@��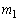 ��
��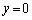 �CR�ɂ�����@��
�CR�ɂ�����@��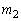 ��
��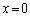
(ii) 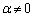 �C�܂�
�C�܂�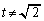 �̂Ƃ��A
�̂Ƃ��A Q��x���W�́A�B��p���āA
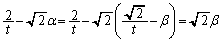 �@(�� �D)
�@(�� �D)���l�ɁAR��x���W��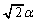 �ł��B
�ł��B
�A���AQ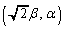 �ɂ�����ڐ�
�ɂ�����ڐ�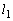 �́A
�́A ���̌X����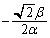 �C����āAQ�ɂ�����@��
�C����āAQ�ɂ�����@��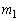 �̌X����
�̌X����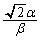 �CQ�ɂ�����@��
�CQ�ɂ�����@��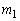 �́A
�́A 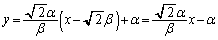 �@����E
�@����E���l��R�ɂ�����@��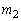 �́A
�́A 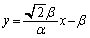 �@����F
�@����F�E�C�F��A�����āA
(ii)�̌��ʂ�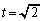 �Ƃ���ƁA
�Ƃ���ƁA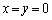 �ƂȂ�̂ŁA(ii)�̌��ʂ�(i)�̌��ʂ��܂�ł��܂��B
�ƂȂ�̂ŁA(ii)�̌��ʂ�(i)�̌��ʂ��܂�ł��܂��B
����āAS�̍��W�́A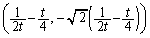 ......[��]
......[��]
(3) S��x���W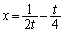 �Cy���W
�Cy���W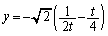 �̊Ԃɂ́A
�̊Ԃɂ́A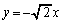 �Ƃ����W������܂��B
�Ƃ����W������܂��B ���x��t�̌�����(���̑������Q��)�ŁA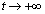 �̂Ƃ�
�̂Ƃ�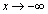 �C
�C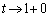 �̂Ƃ�
�̂Ƃ�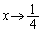
������AS���O���́A����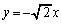 ��
��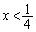 �̕��� ......[��]
�̕��� ......[��]
(4) 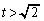 �̂Ƃ��AP�͒���
�̂Ƃ��AP�͒���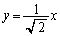 ��
��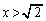 �̕����ɂ���܂��BS�͒���
�̕����ɂ���܂��BS�͒���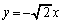 ��
��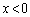 �̕����ɂ���܂��B
�̕����ɂ���܂��B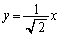 ��
��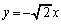 �͒�������̂ŁA��OPS�̖ʐ�
�͒�������̂ŁA��OPS�̖ʐ�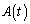 �́A
�́A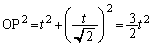 �C
�C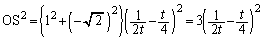 (
(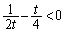 )���A
)���A 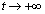 �̂Ƃ��A
�̂Ƃ��A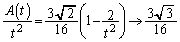 �@(���̋Ɍ����Q��)��
�@(���̋Ɍ����Q��)�� 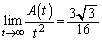 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 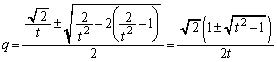
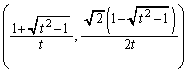 �CR
�CR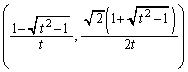 ......[��]
......[��]