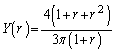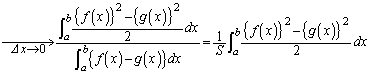大阪市大数学'10年[4]
a,bは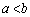 をみたす実数とする。
をみたす実数とする。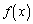 ,
,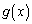 は閉区間
は閉区間 で定義された連続関数で、
で定義された連続関数で、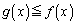 をみたすとする。座標平面上、不等式
をみたすとする。座標平面上、不等式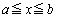 ,
, をみたす点
をみたす点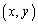 全体からなる図形をAとする。Aの面積Sが正のとき、Aの重心のy座標は、
全体からなる図形をAとする。Aの面積Sが正のとき、Aの重心のy座標は、
で与えられる。この事実を用いて、次の問いに答えよ。
問1 rは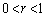 をみたす実数とする。不等式
をみたす実数とする。不等式 ,
,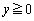 をみたす点
をみたす点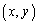 全体からなる図形をBとおく。Bの重心のy座標
全体からなる図形をBとおく。Bの重心のy座標 をrを用いて表せ。
をrを用いて表せ。 問2 tは正の実数とする。不等式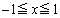 ,
,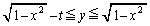 をみたす点
をみたす点 全体からなる図形をCとおく。Cの重心のy座標
全体からなる図形をCとおく。Cの重心のy座標 をtを用いて表せ。
をtを用いて表せ。 問3 問1で得られた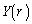 と問2で得られた
と問2で得られた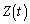 について、
について、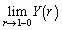 ,
, の大小を比較せよ。
の大小を比較せよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 単なる積分の計算問題ですが、問題文で与えられている式は興味深い式です。
 問1 図形Bは右図黄緑色着色部の部分です。Bの面積
問1 図形Bは右図黄緑色着色部の部分です。Bの面積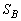 は、半径1の円の面積から半径rの面積を引いて2で割り、
は、半径1の円の面積から半径rの面積を引いて2で割り、Bは の部分に存在し、問題文の重心のy座標の式で、
の部分に存在し、問題文の重心のy座標の式で、 また、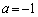 ,
, として、
として、 Bの重心のy座標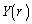 は、
は、 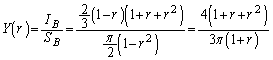 ......[答]
......[答]
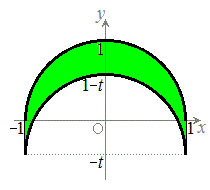 問2 図形Cは右図黄緑色着色部の部分です。Cの面積
問2 図形Cは右図黄緑色着色部の部分です。Cの面積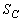 は、半径1の半円の面積
は、半径1の半円の面積 と、横2縦t の長方形の面積を加えて、半円の面積
と、横2縦t の長方形の面積を加えて、半円の面積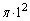 を除き、
を除き、Cは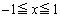 の部分に存在し、問題文の重心のy座標の式で、
の部分に存在し、問題文の重心のy座標の式で、 また、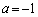 ,
,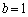 として、
として、 Cの重心のy座標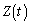 は、
は、 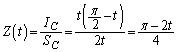 ......[答]
......[答]
(3) (1)より、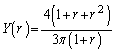
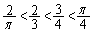 より、
より、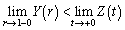 ......[答]
......[答]
追記.問題文の重心のy座標を与える式: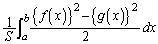 について説明しておきます。
について説明しておきます。 位置xに置かれた幅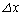 の細長い棒が、
の細長い棒が、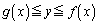 の部分にあるとします。
の部分にあるとします。
棒の重心のy座標は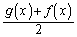 です。棒の質量は棒の面積
です。棒の質量は棒の面積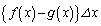 に比例します。
に比例します。
棒全体での重心のy座標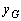 は、質量と各棒の重心のy座標をかけたものを加え合わせ全質量で割ったものになるので、
は、質量と各棒の重心のy座標をかけたものを加え合わせ全質量で割ったものになるので、 ∴  また、この両辺に
また、この両辺に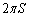 をかけると、
をかけると、
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 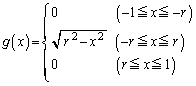
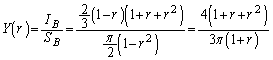 ......[答]
......[答]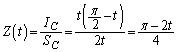 ......[答]
......[答]