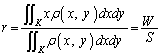���l����H���w'08�N�O��[4]
�A���s����
�̕\���}�`��x���̂܂��ɉ�]���Ăł����]�̂̑̐ς����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�P�Ȃ�v�Z���ł����A���ɂƂ��Ă͌��Ȗ�肩���m��܂���B
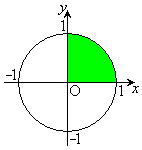
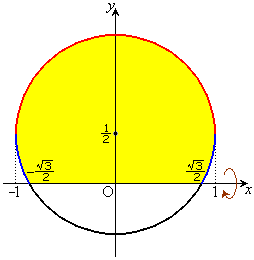 �A���s�����̕\���}�`�͉E�}�̉��F���F�����ł��B�����x���̂܂��ɉ�]��������]�̂̑̐�V�́A�E�}�Ԑ�����(
�A���s�����̕\���}�`�͉E�}�̉��F���F�����ł��B�����x���̂܂��ɉ�]��������]�̂̑̐�V�́A�E�}�Ԑ�����(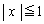 �͈̔͂ɐ}�`������܂�)����]�����Ăł����]�̂̑̐�
�͈̔͂ɐ}�`������܂�)����]�����Ăł����]�̂̑̐�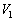 ����A������(
����A������(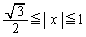 �͈̔͂ɐ}�`������܂�)����]�����Ăł����]�̂̑̐�
�͈̔͂ɐ}�`������܂�)����]�����Ăł����]�̂̑̐�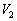 �����������̂ɂȂ�܂��B
�����������̂ɂȂ�܂��B
�Ԑ��������~�̕������́A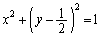 ��y�ɂ��ĉ���
��y�ɂ��ĉ���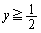 �̕����Ƃ��āA
�̕����Ƃ��āA
����āA�}�`��y ���Ɋւ��đΏ̂Ȃ��Ƃɒ��ӂ��āA
 ��ϕ�
��ϕ�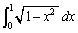 �̔�ϕ����́A
�̔�ϕ����́A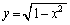 �Ƃ�����
�Ƃ�����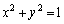 �ƂȂ�̂ŁA��ϕ��́A�E�}�̉��ΐF���F����(���a1�̉~��
�ƂȂ�̂ŁA��ϕ��́A�E�}�̉��ΐF���F����(���a1�̉~��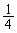 )�̖ʐςɂȂ�A
)�̖ʐςɂȂ�A
�� 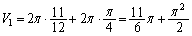
�������̉~�̕������́A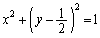 ��y�ɂ��ĉ���
��y�ɂ��ĉ���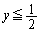 �̕����Ƃ��āA
�̕����Ƃ��āA
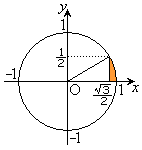 ��ϕ�
��ϕ�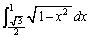 �́A�E�}�̞�F���F�����̖ʐ�(���a1�̉~��
�́A�E�}�̞�F���F�����̖ʐ�(���a1�̉~��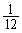 ������
������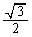 �C����
�C����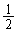 �̎O�p�`�̖ʐς�����������)�ɂȂ�A
�̎O�p�`�̖ʐς�����������)�ɂȂ�A
�� 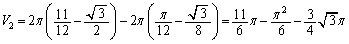
�� 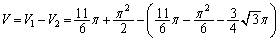
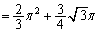 ......[��]
......[��]�NjL�D���̖��̂悤�ȁA�̐ς��ϕ��ɂ�苁�߂���́A��X�l�X�o�肳��Ă��܂����A�ȉ��̋Z�I��m���Ă���ƗL���ȏꍇ������܂��B���̋Z�I���g���Ă��܂��Əo��̈Ӗ����Ȃ��Ȃ�̂ŁA�Z�I���g���Ȃ��悤�ɏo��҂��H�v���Ă��邱�Ƃ������A���̖��ł��g���܂���B 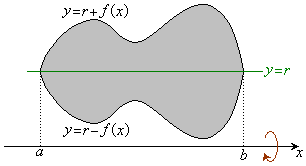 �p�b�v�X�E�M�����_���̒藝(�̓��ʂȏꍇ)�F��]���ɕ��s�Ȓ���(��]���Ƃ̋�����r)�Ɋւ��đΏ̂Ȑ}�`(��]���̕Б��ɂ̂ݑ��݂���)����]���̂܂��ɉ�]���Ăł����]�̂̑̐ς́A�}�`�̖ʐ�S�Ɣ��ar�̉~���̒��������������́F
�p�b�v�X�E�M�����_���̒藝(�̓��ʂȏꍇ)�F��]���ɕ��s�Ȓ���(��]���Ƃ̋�����r)�Ɋւ��đΏ̂Ȑ}�`(��]���̕Б��ɂ̂ݑ��݂���)����]���̂܂��ɉ�]���Ăł����]�̂̑̐ς́A�}�`�̖ʐ�S�Ɣ��ar�̉~���̒��������������́F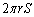 �ɂȂ�B
�ɂȂ�B���ȏ��ɍڂ��Ă���藝�ł͂Ȃ��̂ŁA��[���Ȃ�Ƃ������A���s�^���̒藝�Ɠ��l�A�����̓��Ă̒��Ŏg���đ��v���A�Ƃ����S�z������܂��B
�ł����A�ȒP�ɏؖ��ł���̂ŁA�ؖ����Ă���g���悢�̂ł��B�E�}�̂悤�ȏꍇ�A�D�F��������]�����Ăł����]�̂̑̐�V�́A�O������]��������]�̂̑̐�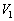 �����������]�������̐�
�����������]�������̐�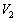 �������悢�킯�ł����A�O���̋Ȑ���
�������悢�킯�ł����A�O���̋Ȑ���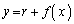 (
(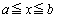 )�ƕ\���ƁA�����̋Ȑ���
)�ƕ\���ƁA�����̋Ȑ���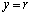 �Ɋւ��đΏ̂Ȃ̂�
�Ɋւ��đΏ̂Ȃ̂�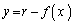 (
(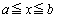 )�ƕ\���܂��B
)�ƕ\���܂��B 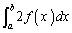 �́A�O���̋Ȑ��Ɠ����̋Ȑ��ŋ��܂ꂽ�����̖ʐ�S�Ȃ̂�(��ϕ��Ɩʐ����Q��)�A
�́A�O���̋Ȑ��Ɠ����̋Ȑ��ŋ��܂ꂽ�����̖ʐ�S�Ȃ̂�(��ϕ��Ɩʐ����Q��)�A�ƂȂ�܂��B
�Ⴆ�A�ȉ~�F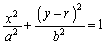 (
(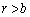 )��x���̂܂��ɉ�]�����Ăł����]�̂̑̐�V�́A�ȉ~�̖ʐς�
)��x���̂܂��ɉ�]�����Ăł����]�̂̑̐�V�́A�ȉ~�̖ʐς�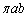 �Ȃ̂ŁA�p�b�v�X�E�M�����_���̒藝���g���ƁA�ϕ��v�Z���s�킸�Ƃ������ɁA
�Ȃ̂ŁA�p�b�v�X�E�M�����_���̒藝���g���ƁA�ϕ��v�Z���s�킸�Ƃ������ɁA �Ƌ��܂��Ă��܂��܂��B���̉�����̖��ł́A���̒藝���g���Ă��܂����̂ł́A�o��̈Ӗ����Ȃ��Ȃ�̂ŁA�킴�Ɖ~��x���Ɍ���点�Ă���킯�ł��B
�֑��̒NjL�D�{��̂悤�ɑΏ̐��̂Ȃ��}�`����]������ꍇ�ɂ́A�����ɂ��̂Ȃ�A�ȉ��̈�ʓI�ȏꍇ�̃p�b�v�X�E�M�����_���̒藝�Ȃ�g���܂��B
�p�b�v�X�E�M�����_���̒藝�F���ʏ�ɒ���l�ƁA���̒���l�ƌ�_�������Ȃ��}�`K���u����Ă���Ƃ��A�}�`K��l�̂܂��ɉ�]���ē������]�̂̑̐ς́A�}�`���d�S�ƒ����Ƃ̋���r�a�Ƃ���~���̒����ɐ}�`�̖ʐ�S�����������́F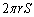 �ɂȂ�B
�ɂȂ�B �������A�{��̏ꍇ�ɂ͏d�S�����߂������L�̉̂悤�Ɍv�Z���Ă��܂������ȒP�ł��B�ނ���A�^�s�����ŕ\�����}�`�̖ʐς�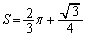 (�~��
(�~��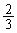 �ƁA���p
�ƁA���p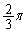 �̓ӎO�p�`)�Ȃ̂ŁA��]�̂̑̐�V��
�̓ӎO�p�`)�Ȃ̂ŁA��]�̂̑̐�V��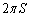 �Ŋ����āA
�Ŋ����āA �Ƃ��āA�d�S��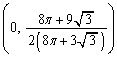 �Ƃ�������ȒP�Ȃ��炢�ł��B
�Ƃ�������ȒP�Ȃ��炢�ł��B
��ʓI�ȏꍇ�̃p�b�v�X�E�M�����_���̒藝�̏ؖ��͈ȉ��̂悤�ȕ��͋C�ɂȂ�܂��B
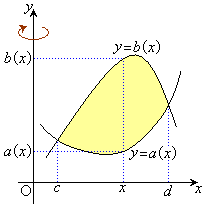 ����l��y ���A�}�`K���A2�Ȑ�
����l��y ���A�}�`K���A2�Ȑ�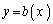 ��
��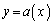 �ɋ��܂ꂽ�̈�
�ɋ��܂ꂽ�̈�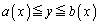 �C
�C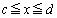 (�E�}�N���[���F����)���Ƃ��܂��B
(�E�}�N���[���F����)���Ƃ��܂��B
�܂��A�}�`K�̎��ʂ��l���܂��B�}�`K�̓_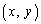 �ɂ�����ʖ��x(�P�ʖʐϓ�����̎���)��
�ɂ�����ʖ��x(�P�ʖʐϓ�����̎���)��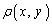 �ł���ꍇ�ɁA���̓_���܂ޕ����̔����ʐ�
�ł���ꍇ�ɁA���̓_���܂ޕ����̔����ʐ�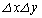 �̎��ʂ�
�̎��ʂ�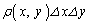 �ł��B�}�`K�̑S���ʂ͐ϕ����āA
�ł��B�}�`K�̑S���ʂ͐ϕ����āA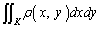 �ŗ^�����܂�(�ϕ����d�ϕ��ƌ�����x��y�̗����Őϕ����邱�Ƃ��Ӗ����܂�)�B
�ŗ^�����܂�(�ϕ����d�ϕ��ƌ�����x��y�̗����Őϕ����邱�Ƃ��Ӗ����܂�)�B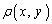 ��x�݂̂̊�
��x�݂̂̊�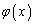 ��y�݂̂̊�
��y�݂̂̊�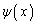 �̐�
�̐�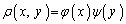 �ƕ\����A�}�`K�̍��Wx�̕�����y�͈̔͂�
�ƕ\����A�}�`K�̍��Wx�̕�����y�͈̔͂�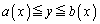 �ƕ\����悤�ȏꍇ�ɂ́A�d�ϕ��́A���y�ɂ��Đϕ����A�ォ��x�ɂ��Đϕ����s���悢�̂ŁA�}�`K��
�ƕ\����悤�ȏꍇ�ɂ́A�d�ϕ��́A���y�ɂ��Đϕ����A�ォ��x�ɂ��Đϕ����s���悢�̂ŁA�}�`K��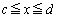 �̕����ɑ��݂���Ƃ��āA
�̕����ɑ��݂���Ƃ��āA 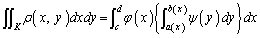 �@����@
�@����@�ƂȂ�܂�(�������Ă��܂����Z�͈͓̔��ł�)�B
�p�b�v�X�E�M�����_���̒藝���z�肵�Ă���}�`K�́A�ώ��Ȑ}�`�Ŗʖ��x�͈��l�ł��B�����ł́A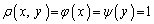 ���Ƃ��܂��B����Ƈ@�́A
���Ƃ��܂��B����Ƈ@�́A ����́A��̋Ȑ��̎����牺�̋Ȑ��̎��������Đϕ����Ă���̂ŁA�Ȑ�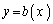 �ƋȐ�
�ƋȐ�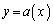 �ň͂܂��}�`�̖ʐ�S�ł�(��ϕ��Ɩʐ����Q��)�B���R�̂��Ƃł����A�}�`K���ʖ��x��1�̋ώ��Ȑ}�`�ł���A�S���ʂ͐}�`�̖ʐ�S�ɂȂ�܂��B
�ň͂܂��}�`�̖ʐ�S�ł�(��ϕ��Ɩʐ����Q��)�B���R�̂��Ƃł����A�}�`K���ʖ��x��1�̋ώ��Ȑ}�`�ł���A�S���ʂ͐}�`�̖ʐ�S�ɂȂ�܂��B
�ʒu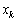 �ɒu���ꂽ����
�ɒu���ꂽ����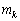 (
(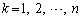 )��n�̕��̂��d�S�̒�`�́A
)��n�̕��̂��d�S�̒�`�́A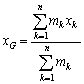 �ł����A���ʂ��A���I�ɕ��z���Ă���ꍇ�ɂ́A
�ł����A���ʂ��A���I�ɕ��z���Ă���ꍇ�ɂ́A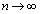 �̋Ɍ����l���敪���ϖ@�ɂ��A����E���q�̃���ϕ��ɂ��܂��B����ɂ��ẮA��L�̂悤�ɁA
�̋Ɍ����l���敪���ϖ@�ɂ��A����E���q�̃���ϕ��ɂ��܂��B����ɂ��ẮA��L�̂悤�ɁA �ƂȂ�܂����A�ʖ��x1�̋ώ��Ȑ}�`�ł���A�}�`�̖ʐ�S�ɂȂ�܂��B���q�ɂ��ẮA�ʖ��x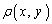 ��x�������Đϕ����邱�ƂɂȂ�A
��x�������Đϕ����邱�ƂɂȂ�A 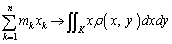 (
(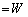 �Ƃ��܂�)
�Ƃ��܂�)�ƂȂ�܂����A�ʖ��x1�̋ώ��Ȑ}�`�ł���A
�ƂȂ�܂��B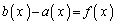 �Ƃ����ƁA
�Ƃ����ƁA �ƂȂ�܂��B�����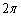 ������������
������������ �́A�Ȑ�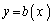 �ƋȐ�
�ƋȐ�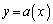 �ň͂܂��}�`��y ���̂܂��ɉ�]�����Ăł����]�̂̑̐�V���~�������ɂ�苁�߂�����(y ���̂܂��̉�]�����Q��)�ł��B�܂�A
�ň͂܂��}�`��y ���̂܂��ɉ�]�����Ăł����]�̂̑̐�V���~�������ɂ�苁�߂�����(y ���̂܂��̉�]�����Q��)�ł��B�܂�A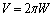 �ł��B
�ł��B
���ǁA���ʂ��ʖ��x1�ŋώ��ɘA���I�ɕ��z���Ă���}�`K�ɂ����āA�d�S�̒�`�́A�d�S��x���W��r�Ƃ��āA �ƂȂ�܂��B���̗��ӂ�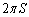 �������āA
�������āA
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 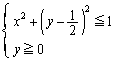
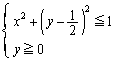
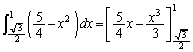
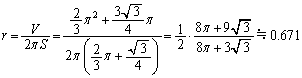
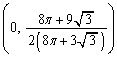 �Ƃ�������ȒP�Ȃ��炢�ł��B
�Ƃ�������ȒP�Ȃ��炢�ł��B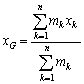 �ł����A���ʂ��A���I�ɕ��z���Ă���ꍇ�ɂ́A
�ł����A���ʂ��A���I�ɕ��z���Ă���ꍇ�ɂ́A