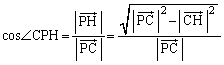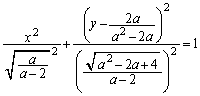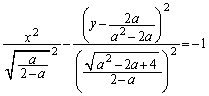�啪��㐔�w'10�N[2]
���S��xyz���W�� �Ŕ��a��1�̋�G�Ɠ_P
�Ŕ��a��1�̋�G�Ɠ_P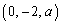 �Ɋւ��āA�_P��ʂ钼������G�Ƌ��L�_�����Ƃ��A���̒�����xy���ʂ̌�_�S�̂����}�`�̊O�`��\�������������߂�B�܂��A���̕��������\���}�`������a�Ɋւ��ĕ��ނ���B
�Ɋւ��āA�_P��ʂ钼������G�Ƌ��L�_�����Ƃ��A���̒�����xy���ʂ̌�_�S�̂����}�`�̊O�`��\�������������߂�B�܂��A���̕��������\���}�`������a�Ɋւ��ĕ��ނ���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�~���ʂŐ����Ƃ��̐����2���Ȑ��ł��B
��G�̒��S��C�C�_P��ʂ钼���Ƌ�G�Ƃ̋��L�_��A�Cxy���ʂƂ̋��L�_��B�Ƃ��܂��B
C���璼��PA�ɉ��낵�������̑���H�Ƃ���ƁA����PA��C��ʂ�ꍇ�������āA�O�p�`PCH�͒��p�O�p�`�ŁA
���̌��ʂ́A����PA��C��ʂ�ꍇ( )�ɂ��������܂��BH�͋�G�̕\�ʏ�܂��͋����̓_�Ȃ̂ŁA
)�ɂ��������܂��BH�͋�G�̕\�ʏ�܂��͋����̓_�Ȃ̂ŁA �ł����āA
�ł����āA
 �Ȃ̂ŁA
�Ȃ̂ŁA
�� 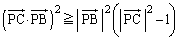 �@����@
�@����@
B��xy���ʏ�̓_�Ȃ̂�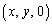 �Ƃ����ƁA
�Ƃ����ƁA
�������@�ɑ�����āA
�W�J���āA
���ӁA�E�ӂ̒萔���ɂ��āA
���A
�O�`�ł́A�s�������ɂ��A�܂�xy���ʏ�̐}�`�ł��邱�Ƃ���A
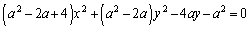 ����
���� 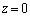 ......[��]�@����@
......[��]�@����@ �̌W���́A
�̌W���́A
 �̌W��
�̌W��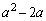 �����A0�C���ɂ���ĕ��ނ��܂��B
�����A0�C���ɂ���ĕ��ނ��܂��B
(i) 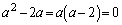
�Ƃ���ƁA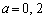
�E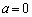 �̂Ƃ��A�@�́A����
�̂Ƃ��A�@�́A����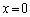
�E �̂Ƃ��A�@�́A
�̂Ƃ��A�@�́A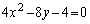
(ii) 
�Ƃ���ƁA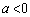 �C
�C
 �̌W���͐��Ȃ̂ŁA�@�́A
�̌W���͐��Ȃ̂ŁA�@�́A (iii) 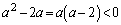
�Ƃ���ƁA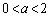
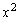 �̌W���͐��Ȃ̂ŁA�@�́A
�̌W���͐��Ȃ̂ŁA�@�́A ������o�Ȑ��ł��B
�ȏ���܂Ƃ߂�ƁA
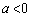 �̂Ƃ��ȉ~�C
�̂Ƃ��ȉ~�C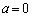 �̂Ƃ������C
�̂Ƃ������C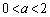 �̂Ƃ��o�Ȑ��C
�̂Ƃ��o�Ȑ��C �̂Ƃ��������C
�̂Ƃ��������C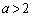 �̂Ƃ��ȉ~ ......[��]
�̂Ƃ��ȉ~ ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B