2���Ȑ��̕����@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
2���Ȑ�C�̕�������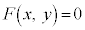 �Ə����ƁAC��x������a�Cy������b���s�ړ�������
�Ə����ƁAC��x������a�Cy������b���s�ړ�������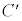 �̕������́A
�̕������́A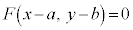
(1) �~���ʂ̗Ő��ɕ��s�ȕ���(�Ő����܂ޕ��ʂ�����)�ʼn~���ʂ��ƁA�f�ʂ����������ł���B
�~���ʂ̎��ɐ����ȕ���(�~���̒�ʂ��܂ޖʁA�~���̒��_��ʂ镽�ʂ�����)�ɁA
�Ő������p���Ȃ��悤�Ɍ����悤�ȕ��ʂʼn~���ʂ��ƁA�f�ʂ��ȉ~���ł���B
�Ő������[���p���Ȃ��悤�Ɍ���镽�ʂʼn~���ʂ��ƁA�f�ʂ��o�Ȑ����ł���B
�ȏ�̈Ӗ��ŁA2���Ȑ����~���Ȑ��ƌĂ��B
(2) �œ_F�ƁA�_F��ʉ߂��Ȃ�����l������Ƃ��A�Ȑ���̓_P��F�Ƃ̋���FP�ƁA�Ȑ���_P����l�܂ł̋���PH�Ƃ̔�F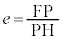 �����S���ƌ����B
�����S���ƌ����B
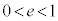 �C�܂�A
�C�܂�A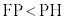 �ƂȂ�Ȑ����ȉ~
�ƂȂ�Ȑ����ȉ~
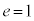 �C�܂�A
�C�܂�A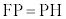 �ƂȂ�Ȑ���������
�ƂȂ�Ȑ���������
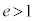 �C�܂�A
�C�܂�A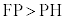 �ƂȂ�Ȑ����o�Ȑ�
�ƂȂ�Ȑ����o�Ȑ�
(3) 2���Ȑ��̕������̈�ʌ`�F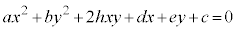 �@���(��)�@�ɑ��āA�s��
�@���(��)�@�ɑ��āA�s��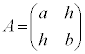 ���l����B�ȉ��A�s���ŕ��ނ��āA
���l����B�ȉ��A�s���ŕ��ނ��āA
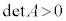 �̂Ƃ��A(��)�́A�ȉ~��\�����A1�_��\�����A�����\���Ȃ��B
�̂Ƃ��A(��)�́A�ȉ~��\�����A1�_��\�����A�����\���Ȃ��B
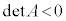 �̂Ƃ��A(��)�́A�o�Ȑ���\�����A�����2������\���B
�̂Ƃ��A(��)�́A�o�Ȑ���\�����A�����2������\���B
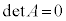 �̂Ƃ��A(��)�́A��������\�����A���s2������\�����A1������\�����A�����\���Ȃ��B
�̂Ƃ��A(��)�́A��������\�����A���s2������\�����A1������\�����A�����\���Ȃ��B
2���Ȑ�C�F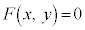 ��̓_�̍��W��
��̓_�̍��W��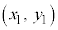 �CC��x������a�Cy������b���s�ړ�������
�CC��x������a�Cy������b���s�ړ�������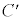 �F
�F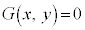 ��̓_�̍��W��
��̓_�̍��W��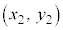 �Ƃ���ƁA
�Ƃ���ƁA
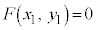 �C
�C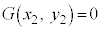
�܂��A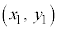 ��x������a�Cy������b���s�ړ��������_��
��x������a�Cy������b���s�ړ��������_��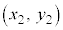 ���Ƃ���A
���Ƃ���A
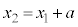 �C
�C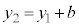
�܂�A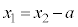 �C
�C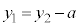
������A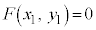 �ɑ������ƁA
�ɑ������ƁA
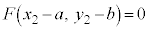
���āA���̎��́A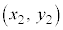 �Ɋւ���������ł����A
�Ɋւ���������ł����A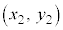 ���������ׂ��������́A
���������ׂ��������́A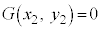 �łȂ���Ȃ�܂���B�Ƃ������Ƃ́A
�łȂ���Ȃ�܂���B�Ƃ������Ƃ́A
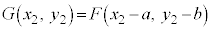
�ł����āA�Ȑ�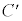 �̕������́A
�̕������́A
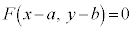
�Ƃ������ƂɂȂ�܂��B
(1) ���_O��ʂ�A�����x�N�g����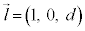 (
(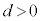 )�ƂȂ��ԓ��̒��������Ƃ���~���ʏ�̓_P���w���x�N�g����
)�ƂȂ��ԓ��̒��������Ƃ���~���ʏ�̓_P���w���x�N�g����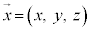 �Ƃ��A�~���ʂ̗Ő�(�~���ʏ�̒����A�~���̒��_��ʂ�)�ƁA�~���̎��Ƃ̂Ȃ��p��θ (
�Ƃ��A�~���ʂ̗Ő�(�~���ʏ�̒����A�~���̒��_��ʂ�)�ƁA�~���̎��Ƃ̂Ȃ��p��θ (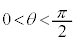 �Cθ �͂��ׂĂ̗Ő��ɑ��Ĉ��ł�)�Ƃ���A
�Cθ �͂��ׂĂ̗Ő��ɑ��Ĉ��ł�)�Ƃ���A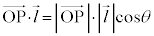 �����藧���܂�(�����A��ԃx�N�g�����Q��)�B
�����藧���܂�(�����A��ԃx�N�g�����Q��)�B
�� 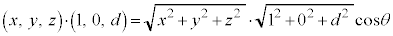
2�悵�āA
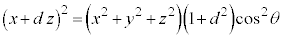 �@����@�@(���ꂪ�~���ʂ̕�������^���܂�)
�@����@�@(���ꂪ�~���ʂ̕�������^���܂�)
���̉~���ʂ��Az���ɐ���(xy���ʂɕ��s)�ŁA�~���̒��_(���_O�ł�)��ʂ�Ȃ����ʁF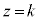 (
(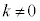 )�Őؒf�����Ƃ��̐���̐}�`�ׂ܂��B�@�ŁA
)�Őؒf�����Ƃ��̐���̐}�`�ׂ܂��B�@�ŁA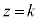 �Ƃ����āA��������ƁA
�Ƃ����āA��������ƁA
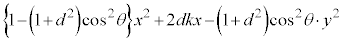
�@�@�@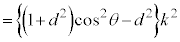
�� 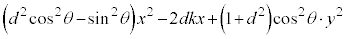
�@�@�@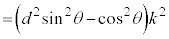 �@����A
�@����A
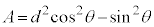 �C
�C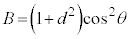 �Ƃ����ƁA�A�́A
�Ƃ����ƁA�A�́A
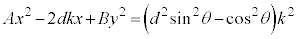 �@����B
�@����B
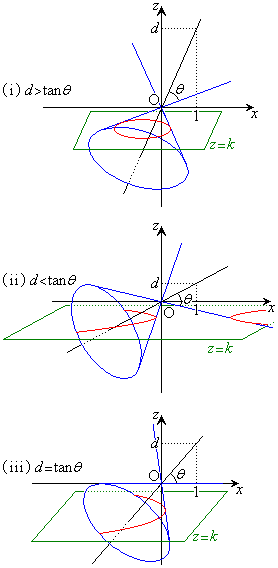 (i)
(i) 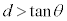 �̂Ƃ��A
�̂Ƃ��A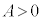 �C���̂Ƃ��A�~���ʂ�ؒf���镽�ʁF
�C���̂Ƃ��A�~���ʂ�ؒf���镽�ʁF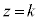 �́A�~���̒�ʂƁA�Ő������p���Ȃ��Č����܂��B
�́A�~���̒�ʂƁA�Ő������p���Ȃ��Č����܂��B
�B���A
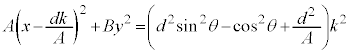
�@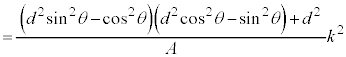
�@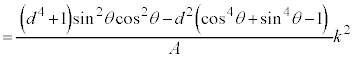
�@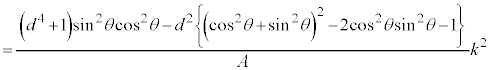
�@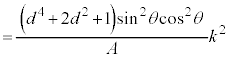
�@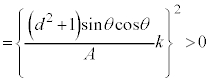 �@(
�@(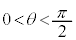 )
)
����āA�B�́A����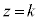 ��ŁA
��ŁA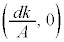 �𒆐S�Ƃ����ȉ~��\���܂��B
�𒆐S�Ƃ����ȉ~��\���܂��B
(ii) 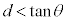 �̂Ƃ��A
�̂Ƃ��A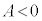 �C���̂Ƃ��A�~���ʂ�ؒf���镽�ʁF
�C���̂Ƃ��A�~���ʂ�ؒf���镽�ʁF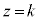 �́A�~���̒�ʂƁA�Ő������[���p���Ȃ��Č����܂��B
�́A�~���̒�ʂƁA�Ő������[���p���Ȃ��Č����܂��B
���̂Ƃ��́A�ȉ~�̂Ƃ��Ɠ��l�ɂ��āA�B�́A����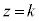 ��ŁA�o�Ȑ���\���܂��B
��ŁA�o�Ȑ���\���܂��B
(iii) 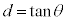 �̂Ƃ��A
�̂Ƃ��A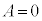 �C���̂Ƃ��A�~���ʂ�ؒf���镽�ʁF
�C���̂Ƃ��A�~���ʂ�ؒf���镽�ʁF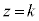 �́A�Ő��ƕ��s�ł��B
�́A�Ő��ƕ��s�ł��B
�B���A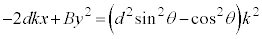
�� 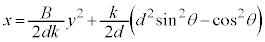
����́A����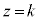 ��ŁA��������\���܂��B
��ŁA��������\���܂��B
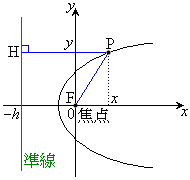 (2) ���W���ʏ�ɁA��_F
(2) ���W���ʏ�ɁA��_F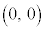 �C�蒼��l�F
�C�蒼��l�F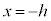 (
(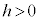 )���Ƃ�A�Ȑ�C���1�_P
)���Ƃ�A�Ȑ�C���1�_P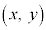 ����l�ɉ��낵�������̑���H�Ƃ��܂��B
����l�ɉ��낵�������̑���H�Ƃ��܂��B
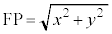 �C�_P��l�Ƃ̋����F
�C�_P��l�Ƃ̋����F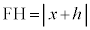
�_P���A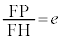 (e�F���C
(e�F���C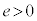 )�����Ƃ��܂��B
)�����Ƃ��܂��B
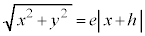
���ӂ�2�悵�āA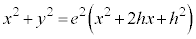
�������āA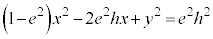 �@����C
�@����C
(i) 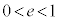 �̂Ƃ��A
�̂Ƃ��A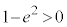 �ł��B
�ł��B
�C���A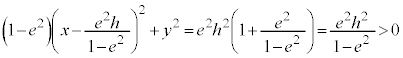
����́A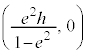 �𒆐S�Ƃ����ȉ~��\���܂��B
�𒆐S�Ƃ����ȉ~��\���܂��B
(ii) 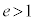 �̂Ƃ��A
�̂Ƃ��A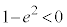 �ł��B
�ł��B
�ȉ~�̂Ƃ��Ɠ��l�ɁA�C�́A�o�Ȑ���\���܂��B
(iii) 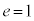 �̂Ƃ��A�C�́A
�̂Ƃ��A�C�́A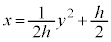 �ƂȂ�A��������\���܂��B
�ƂȂ�A��������\���܂��B
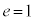 �̂Ƃ��A
�̂Ƃ��A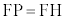 �ł����A������������̒�`���̂��̂ł��B
�ł����A������������̒�`���̂��̂ł��B
(2���Ȑ��̕���(����2)�ւÂ�)
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 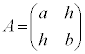 ���l����B�ȉ��A�s���ŕ��ނ��āA
���l����B�ȉ��A�s���ŕ��ނ��āA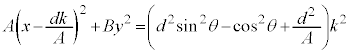
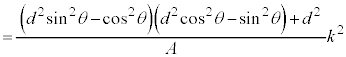
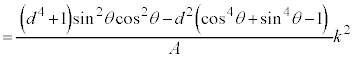
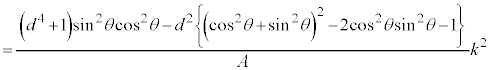
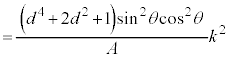
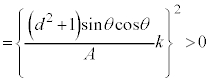 �@(
�@(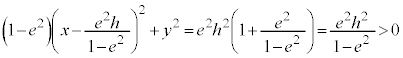
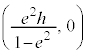 �𒆐S�Ƃ����ȉ~��\���܂��B
�𒆐S�Ƃ����ȉ~��\���܂��B