2���Ȑ��̕���(����2)
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
2���Ȑ��̕��ނ̂Â��ł��B
(3) 2���Ȑ��̕������͈�ʓI�ɁA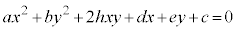 �@���(��)�@�ƕ\�����Ƃ��ł��܂��B
�@���(��)�@�ƕ\�����Ƃ��ł��܂��B
(��)���Ȑ���\���Ƃ��́A������1�_�ɂȂ�ꍇ�������ƁA�ȉ~���o�Ȑ����������Ɍ����邱�Ƃ��m���߂Ă݂܂��B
�܂��A(��)���s���p���ď��������܂�(�s���A�s��̐����Q��)�B
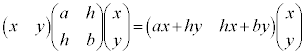
�@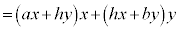
�@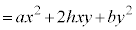
���A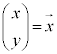 �C
�C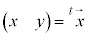 (t�t���͓]�u�s����Ӗ����܂��A��x�N�g���ƍs�x�N�g���̓���ւ��ł�)�C
(t�t���͓]�u�s����Ӗ����܂��A��x�N�g���ƍs�x�N�g���̓���ւ��ł�)�C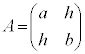 �C
�C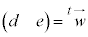 �Ƃ��āA(��)�́A
�Ƃ��āA(��)�́A
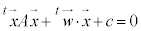
�Ə����܂��B�Ƃ���ŁA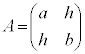 �͎����𐬕��Ƃ���Ώ̍s��(
�͎����𐬕��Ƃ���Ώ̍s��(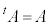 �����s��A�Ίp���������ɂ��ĉE��ƍ����ɑΏ̂ɐ���������)�Ȃ̂ŁA�����s��M(
�����s��A�Ίp���������ɂ��ĉE��ƍ����ɑΏ̂ɐ���������)�Ȃ̂ŁA�����s��M(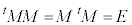 �C�܂�A
�C�܂�A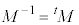 �����s��A2���̐����s��ł́A��]�ړ���\���s��ƁA���_��ʂ钼���Ɋւ���܂�Ԃ���\���s��Ɍ�����A
�����s��A2���̐����s��ł́A��]�ړ���\���s��ƁA���_��ʂ钼���Ɋւ���܂�Ԃ���\���s��Ɍ�����A
1���ϊ�(����2)���Q��)�ɂ���āA�Ίp�����邱�Ƃ��ł��܂�(�X�y�N�g���������Q��)�B�܂�A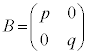 (p�Cq�́AA���ŗL�l)�Ƃ��āA
(p�Cq�́AA���ŗL�l)�Ƃ��āA
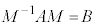
�ƂȂ�悤�ȁA�����s��M���Ƃ邱�Ƃ��ł��܂�(M�́AA�̌ŗL�x�N�g���ő傫��1�̃x�N�g�������ɕ��ׂ��s��)�B
���̂Ƃ��A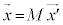 �C�܂�A
�C�܂�A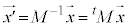 �ƂȂ�
�ƂȂ�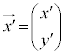 ���Ƃ�ƁA
���Ƃ�ƁA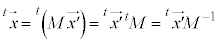 ���A
���A
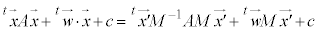
�@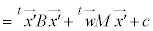
�����ŁA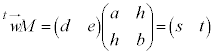 �C�܂�A
�C�܂�A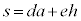 �C
�C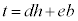 �Ƃ����ƁA
�Ƃ����ƁA
�@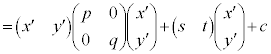
�@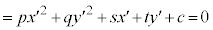 �@����D
�@����D
�������āA(��)�̒��ɂ�����xy�̍����������Ƃ��ł��܂��BM�͉�]�ړ��܂��͐܂�Ԃ���\���̂ŁA�D�ɂ����Ă��A�Ȑ�(����)�̌`��ɂ͕ω��͂���܂���B
�����ŁA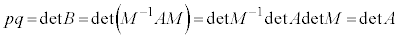 �@(�t�s�����Q��)
�@(�t�s�����Q��)
(i) p�Cq���������ŁA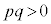 �C�܂�A
�C�܂�A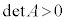 �̂Ƃ��A�D�́A
�̂Ƃ��A�D�́A
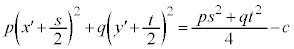
�E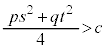 �̂Ƃ��A(��)�́A�ȉ~��\���܂��B
�̂Ƃ��A(��)�́A�ȉ~��\���܂��B
�E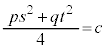 �̂Ƃ��A(��)�́A1�_
�̂Ƃ��A(��)�́A1�_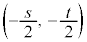 �ƂȂ�܂��B
�ƂȂ�܂��B
�E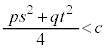 �̂Ƃ��A(��)�́A�����\���܂���B
�̂Ƃ��A(��)�́A�����\���܂���B
(ii) p�Cq���ٕ����ŁA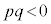 �C�܂�A
�C�܂�A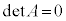 �̂Ƃ��A�ȉ~�̂Ƃ��Ɠ��l�ɂ��āA
�̂Ƃ��A�ȉ~�̂Ƃ��Ɠ��l�ɂ��āA
�E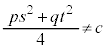 �̂Ƃ��A(��)�́A�o�Ȑ���\���܂��B
�̂Ƃ��A(��)�́A�o�Ȑ���\���܂��B
�E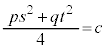 �̂Ƃ��A(��)�́A
�̂Ƃ��A(��)�́A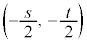 �Ō����2������\���܂��B
�Ō����2������\���܂��B
(iii) p�Cq�̂����ꂩ����A���邢�́A������0�ŁA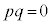 �C�܂�A
�C�܂�A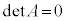 �̂Ƃ��A
�̂Ƃ��A
�E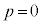 �C
�C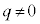 �̂Ƃ��́A
�̂Ƃ��́A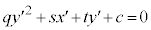
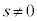 �Ȃ�A
�Ȃ�A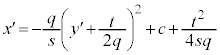 ��(��)����������\���܂��B
��(��)����������\���܂��B
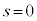 �̂Ƃ��́A
�̂Ƃ��́A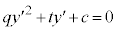
���ʎ��F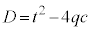 �Ƃ���(2�����������Q��)�A
�Ƃ���(2�����������Q��)�A
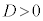 �̂Ƃ��ɂ́A(��)�͕��s2������\���A
�̂Ƃ��ɂ́A(��)�͕��s2������\���A
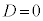 �̂Ƃ��ɂ́A(��)��1������\���A
�̂Ƃ��ɂ́A(��)��1������\���A
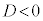 �̂Ƃ��ɂ́A(��)�͉����\���܂���B
�̂Ƃ��ɂ́A(��)�͉����\���܂���B
�E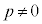 �C
�C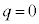 �̂Ƃ����A���l�ł��B
�̂Ƃ����A���l�ł��B
�E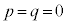 �̂Ƃ��ɂ́A
�̂Ƃ��ɂ́A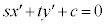
(��)��1������\���܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 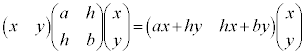
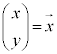 �C
�C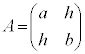 �C
�C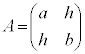 �͎����𐬕��Ƃ���Ώ̍s��(
�͎����𐬕��Ƃ���Ώ̍s��(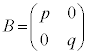 (p�Cq�́AA���ŗL�l)�Ƃ��āA
(p�Cq�́AA���ŗL�l)�Ƃ��āA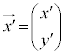 ���Ƃ�ƁA
���Ƃ�ƁA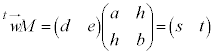 �C�܂�A
�C�܂�A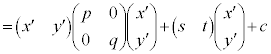
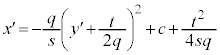 ��(��)����������\���܂��B
��(��)����������\���܂��B