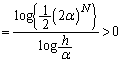���k�嗝�n���w'10�N���[4]
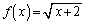 �Ƃ��āA����
�Ƃ��āA����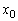 �C
�C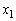 �C
�C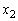 �C��� ��
�C��� ��
�Œ�`����B�ȉ��̖₢�ɓ�����B
(1) ���ׂĂ̎��R��n�ɑ���
�����藧���Ƃ������B
(2) ���ׂĂ̎��R��n�ɑ���
�����藧���Ƃ������B
(3) ���ׂĂ̎��R��n�ɑ���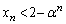 �������̒萔α�̂����A�ő�̂��̂����߂�B
�������̒萔α�̂����A�ő�̂��̂����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(3)�́A(2)����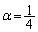 �Ɨ\�������̂ŁA�����l���邱�Ƃɂ��܂��B���Z�͈̔͂ł͌�������肩���m��܂���B
�Ɨ\�������̂ŁA�����l���邱�Ƃɂ��܂��B���Z�͈̔͂ł͌�������肩���m��܂���B
(a) 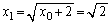 ���
���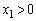 �ł��B
�ł��B 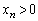 �ł���A
�ł���A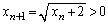
����āA�A�[�I�ɁA���ׂĂ̎��R��n�ɑ��āA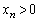 �ł��B
�ł��B(b) 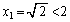
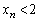 �Ɖ��肷��ƁA
�Ɖ��肷��ƁA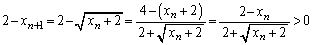 �@����@
�@����@�� 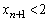 ����āA�A�[�I�ɁA���ׂĂ̎��R��n�ɑ��āA
����āA�A�[�I�ɁA���ׂĂ̎��R��n�ɑ��āA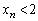 �ł��B
�ł��B (c) 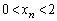 ���A
���A �� 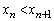 ����āA���ׂĂ̎��R��n�ɑ��āA
����āA���ׂĂ̎��R��n�ɑ��āA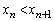 �ł��B
�ł��B (d) 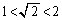 ���A
���A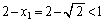
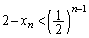 �Ɖ��肷��ƁA(c)�ɂ��
�Ɖ��肷��ƁA(c)�ɂ��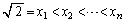 �ƂȂ�A
�ƂȂ�A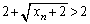 �Ȃ̂ŁA�@�Ɠ��l�ɁA
�Ȃ̂ŁA�@�Ɠ��l�ɁA�� 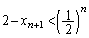 ����āA�A�[�I�ɁA���ׂĂ̎��R��n�ɑ��āA
����āA�A�[�I�ɁA���ׂĂ̎��R��n�ɑ��āA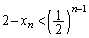
(a)�`(d)���A���ׂĂ̎��R��n�ɑ��āA
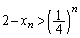 �Ɖ��肷��ƁA
�Ɖ��肷��ƁA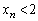 ���
���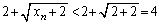 �ƂȂ�̂ŁA�@�Ɠ��l�ɁA
�ƂȂ�̂ŁA�@�Ɠ��l�ɁA�� 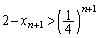 ����āA�A�[�I�ɁA���ׂĂ̎��R��n�ɑ��āA
����āA�A�[�I�ɁA���ׂĂ̎��R��n�ɑ��āA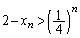 �C�܂�A
�C�܂�A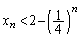
(3) (2)���A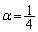 ���낤�A�Ƃ����@���͂��܂����A��������A
���낤�A�Ƃ����@���͂��܂����A��������A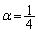 �ƒf��ł���̂����l���Ȃ��Ă͂����܂���B
�ƒf��ł���̂����l���Ȃ��Ă͂����܂���B �����ŁA�u���ׂĂ̎��R��n�ɑ���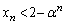 �������̒萔α�̂����A�ő�̂��̂����߂�B�v�Ƃ�����蕶����A����
�������̒萔α�̂����A�ő�̂��̂����߂�B�v�Ƃ�����蕶����A����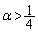 �ƂȂ��
�ƂȂ��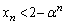 ���������Ȃ��Ȃ�A�Ƃ������Ƃ��������Ƃɂ��܂��B�܂�A
���������Ȃ��Ȃ�A�Ƃ������Ƃ��������Ƃɂ��܂��B�܂�A
�u���ׂĂ̎��R��n�ɑ���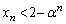 �̂Ƃ��A
�̂Ƃ��A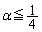 �v�Ƃ�����������A�u
�v�Ƃ�����������A�u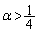 �̂Ƃ��A
�̂Ƃ��A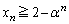 �@����A�@�ƂȂ鎩�R��n�����݂���v���������Ƃ�ڕW�ɂ��܂��B
�@����A�@�ƂȂ鎩�R��n�����݂���v���������Ƃ�ڕW�ɂ��܂��B
�܂��A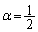 �C
�C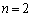 �̂Ƃ��A
�̂Ƃ��A �܂�A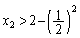 �ƂȂ�̂ŁA
�ƂȂ�̂ŁA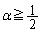 �ł���A�A�������R��n�����݂���͖̂��炩�ł��B�ȉ��A
�ł���A�A�������R��n�����݂���͖̂��炩�ł��B�ȉ��A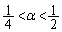 �̏ꍇ���l���܂��B
�̏ꍇ���l���܂��B
�Ƃ���ŁA�@�ɂ����āA(1)�C(2)�ł��������悤�ɁA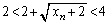 �ł��B�܂��A(1)�̌��ʂ�
�ł��B�܂��A(1)�̌��ʂ�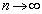 �Ƃ���ƁA
�Ƃ���ƁA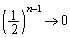 (���䐔��̋Ɍ����Q��)�ł��邱�ƂƁA�͂��݂����̌������A
(���䐔��̋Ɍ����Q��)�ł��邱�ƂƁA�͂��݂����̌������A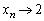 �ƂȂ�܂��Bα��
�ƂȂ�܂��Bα��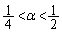 (
(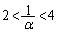 )���������Ȃ�����ł����Ă��An���\���ɑ傫���Ƃ�A
)���������Ȃ�����ł����Ă��An���\���ɑ傫���Ƃ�A 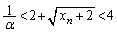 �@����B
�@����B�ƂȂ�悤��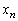 ���K�����݂��܂��B�Ȃ��Ȃ�A�B���݂������R��n�����݂��Ȃ��A�܂�A���ׂĂ̎��R��n�ɂ��āA
���K�����݂��܂��B�Ȃ��Ȃ�A�B���݂������R��n�����݂��Ȃ��A�܂�A���ׂĂ̎��R��n�ɂ��āA �ł���Ɖ��肷��(�w���@�ɂ��ẮA�ؖ��̋Z�I���Q��)�ƁA �����ŁA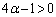 �Ȃ̂ŁA
�Ȃ̂ŁA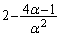 �́A2���������Ȃ���萔�ł��B�Ƃ������Ƃ́A
�́A2���������Ȃ���萔�ł��B�Ƃ������Ƃ́A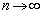 �̂Ƃ�
�̂Ƃ�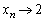 �ɂȂ蓾���A�s�����ł��B
�ɂȂ蓾���A�s�����ł��B
�܂�A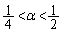 �̂Ƃ��A�B�������R��n���K�����݂��܂��B���̂Ƃ��A�B���A
�̂Ƃ��A�B�������R��n���K�����݂��܂��B���̂Ƃ��A�B���A 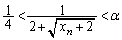 �@����C
�@����C�ƂȂ�܂��B�B�������R��n�͕������݂��邩���m��܂��A���̂����̍ŏ���n (����n��N�Ƃ��܂�)�ɑ���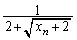 �̒l��h�Ƃ����܂��B�܂�A
�̒l��h�Ƃ����܂��B�܂�A 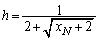 (
(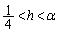 )�@����D
)�@����D(1)���A���ׂĂ̎��R���ɂ���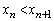 �Ȃ̂ŁA
�Ȃ̂ŁA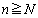 �ƂȂ邷�ׂĂ̎��R��n�ɂ��āA
�ƂȂ邷�ׂĂ̎��R��n�ɂ��āA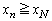 ���A
���A 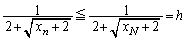 �@(�܂�A
�@(�܂�A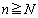 �ƂȂ邷�ׂĂ̎��R��n�ɂ��āA�B�C�C�����������)
�ƂȂ邷�ׂĂ̎��R��n�ɂ��āA�B�C�C�����������)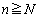 �ƂȂ�悤�Ȏ��R��n�ɂ��āA�@�Ɠ��l�ɂ��āA
�ƂȂ�悤�Ȏ��R��n�ɂ��āA�@�Ɠ��l�ɂ��āA������J��Ԃ��p���āA
�܂��A(1)�̌��ʂ�p���āA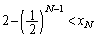 �C�����A
�C�����A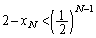
�� 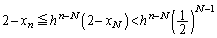 �@����E
�@����E
�����ŁA 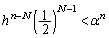 �@����F
�@����F�ƂȂ��Ă����Ɠs�����悢�̂ł����A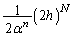 �𗼕ӂɂ�����ƁA
�𗼕ӂɂ�����ƁA 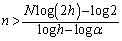 �@����G
�@����G����āA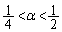 �ƂȂ�α�ɑ��āC�C�����悤�Ȏ��R��N�C�D�����悤��h�C�G�����悤�Ȏ��R��n (
�ƂȂ�α�ɑ��āC�C�����悤�Ȏ��R��N�C�D�����悤��h�C�G�����悤�Ȏ��R��n (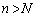 )���Ƃ�ƁA�E�C�F���A
)���Ƃ�ƁA�E�C�F���A ����āA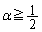 �̂Ƃ������킹�āA
�̂Ƃ������킹�āA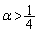 �̂Ƃ��A
�̂Ƃ��A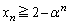 �������R��n�����݂��܂��B
�������R��n�����݂��܂��B
�]���āA���̖���̑�A�u���ׂĂ̎��R��n�ɑ���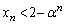 �̂Ƃ��A
�̂Ƃ��A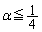 �v���������A���ׂĂ̎��R��n�ɑ���
�v���������A���ׂĂ̎��R��n�ɑ���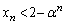 �������̒萔α�̂����A�ő�̂��̂́A
�������̒萔α�̂����A�ő�̂��̂́A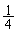 ......[��]
......[��] ���ӁD�G�������R��n (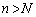 )�����݂��邩�A�Ƃ����S�z������܂����A
)�����݂��邩�A�Ƃ����S�z������܂����A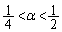 �̂Ƃ��A
�̂Ƃ��A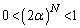 ���A
���A ���A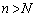 �ł��B
�ł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B