���l����H���w'10�N���[5]
2�̐��� �C
�C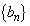 ��
��
�Œ�߂�B���̖₢�ɓ�����B
(1) 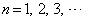 �ɑ��āA
�ɑ��āA 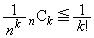 �@�@
�@�@
�������B
(2) 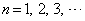 �ɑ��āA
�ɑ��āA �������B
�������B (3) n��2�ȏ�̎��R���Ƃ���B �ł��鎩�R��k�ɑ��āA
�ł��鎩�R��k�ɑ��āA �������B
(4)  �ɑ��āA
�ɑ��āA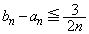 �������B�������A
�������B�������A (
(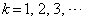 ) ���ؖ��Ȃ��ɗp���Ă悢�B
) ���ؖ��Ȃ��ɗp���Ă悢�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�ȉ��ł́A �Ƃ��܂��B(1)(4)�ł́A�W���̒�`�F
�Ƃ��܂��B(1)(4)�ł́A�W���̒�`�F (�g�ݍ��킹���Q��)���g���܂��B
(�g�ݍ��킹���Q��)���g���܂��B
(1) 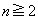 ����
���� 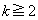 �̂Ƃ��A
�̂Ƃ��A  ����
���� 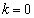 �̂Ƃ��A
�̂Ƃ��A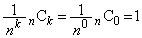 �C
�C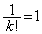
 ����
���� 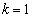 �̂Ƃ��A
�̂Ƃ��A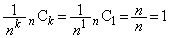 �C
�C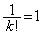
 �̂Ƃ��A
�̂Ƃ��A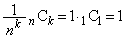 �C���̂Ƃ��A
�C���̂Ƃ��A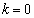 �܂���
�܂���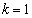 �Ȃ̂ŁA
�Ȃ̂ŁA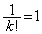
�ȏ���A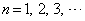 �ɑ��āA
�ɑ��āA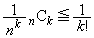 �@
�@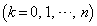
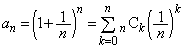 �@����@
�@����@(1)�̌��ʂ�p���āA
(�T) 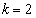 �̂Ƃ��A
�̂Ƃ��A ����āA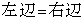 �ł���A�^�s�����͐������܂��B
�ł���A�^�s�����͐������܂��B (�U) 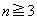 ����
����  (
(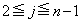 )�̂Ƃ��A�^�s��������������Ƃ��܂��B�܂�A
)�̂Ƃ��A�^�s��������������Ƃ��܂��B�܂�A ���̂Ƃ��A
 �@����A
�@����A���̍��ӂ́A
�A���ӂ� ��������ƁA
��������ƁA ���
���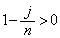 �Ȃ̂ŁA
�Ȃ̂ŁA ���̍��ӂ́A
����āA
�� 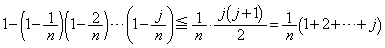 ����āA
����āA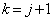 �̂Ƃ��ɂ��A�^�s�����͐������܂��B
�̂Ƃ��ɂ��A�^�s�����͐������܂��B (�T)�C(�U)���An��2�ȏ�̎��R���Ƃ���ƁA �ł��鎩�R��k�ɑ��āA�^�s�������������܂��B
�ł��鎩�R��k�ɑ��āA�^�s�������������܂��B ���D �̂Ƃ���
�̂Ƃ��� �Ɍ�����̂ŁA(�T)�����Ŋ������Ă��邱�Ƃɒ��ӂ��Ă��������B
�Ɍ�����̂ŁA(�T)�����Ŋ������Ă��邱�Ƃɒ��ӂ��Ă��������B
(4)  �̂Ƃ��A�@�Ɠ��l�ɂ��āA
�̂Ƃ��A�@�Ɠ��l�ɂ��āA  �@(���D
�@(���D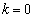 �̂Ƃ����J�b�R����0�ł�)
�̂Ƃ����J�b�R����0�ł�)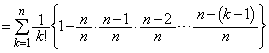 �@(���D
�@(���D �̂Ƃ����J�b�R����0�ł�)
�̂Ƃ����J�b�R����0�ł�)
�a���Ƃ�Ƃ�k�������͈͂�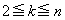 �Ƃ��Ă���̂ŁA��L��
�Ƃ��Ă���̂ŁA��L��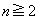 �̏ꍇ�ł��B(3)�̌��ʂ�p���āA
�̏ꍇ�ł��B(3)�̌��ʂ�p���āA ��蕶�̃q���g�F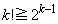 (
( )��p���āA�ȉ��A
)��p���āA�ȉ��A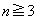 �̂Ƃ��A
�̂Ƃ��A 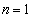 �̂Ƃ��A
�̂Ƃ��A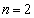 �̂Ƃ��A
�̂Ƃ��A����āA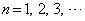 �ɑ��āA
�ɑ��āA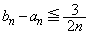
�NjL�D(2)�̌��ʂƍ��킹�āA �ƂȂ�܂����A�����ŁA
�ƂȂ�܂����A�����ŁA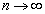 �Ƃ���ƁA
�Ƃ���ƁA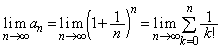 �ƂȂ邱�Ƃ��킩��܂��B
�ƂȂ邱�Ƃ��킩��܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 
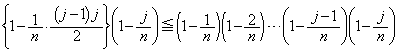

 �@(���D
�@(���D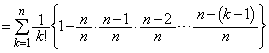 �@(���D
�@(���D